静电场中静电屏蔽的Ansoft求解
2011-08-16杨俊秀赵文来
杨俊秀,赵文来,鲍 佳
(浙江理工大学信息电子学院,浙江杭州 310018)
“电磁场与电磁波”是理工科院校的一门必修课程。如果在授课中,从物理或实例上阐述场,并通过相关的仿真软件如Ansoft来分析,场分布、电感、电容、场力、涡流、电路及能量等问题,可加深学生对电磁场理论及其应用的理解[1]。
本文以静电屏蔽为例,给出金属罩接地与不接地两种情况下,对空间电场的影响,并绘出其空间电位的变化曲线。
电磁问题的描述如下:①自由空间中一实心圆球,其上加载100V的电压,且外罩一金属罩;②设无限远处的电位为零③求空间电位变化规律,并画出电场沿径向的变化曲线;④若金属罩不闭合,结果将如何。
任何的电磁问题都可以转换为求解满足一定条件的麦克斯韦方程组,我们先给出理论上的解的表达式,再给出基于Ansoft的分析求解过程。
1 理论求解
静电屏蔽属于静电场或恒定电场问题,且满足球对称条件,故可根据高斯定理求解满足题目边界要求的拉普拉斯方程,此处给出高斯定理的求解。
[解]:为了给出具体表达式,现设金属球半径为a,金属罩内、外表面半径分别为b,c,金属球带电量为q。
依据题目中源的结构,建立球坐标系,坐标原点在实心金属球心。则球心在原点,半径为r的球面上,电场大小相等,且方向为径向。我们可利用高斯定理:,求解结果为
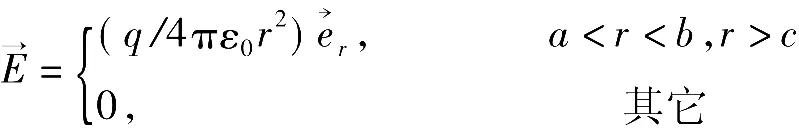
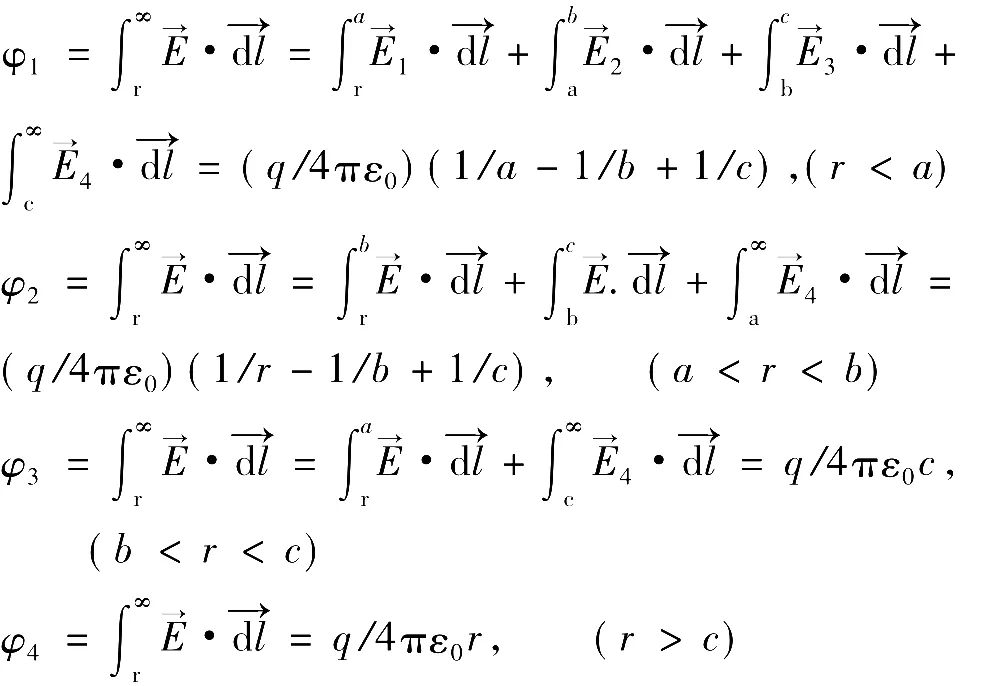
由以上表达式可看出,r<a,b<r<c空间电位为常数,其它与该点到原点的径向距离成反比,且在分界面上均满足电位连续性,电场不连续。
2 Ansoft求解
电磁场问题的实质是求解给定边界条件下的麦克斯韦方程组及方程组演化的其他偏微分方程[2]。从求解的技术手段上分,有解析求解及数值求解。对简单问题可得到方程的解析解,若模型复杂,则很难获得模型的解析解。随计算工具的发展,电磁场数值计算深入各个领域,有限元法是常用的数值方法,其中Ansoft公司的Maxwell 3D/2D就是一款优秀的电磁分析软件[3,4]。
下面给出求解过程[5]:
1)基于Maxwell 2D,为简化运算采用图1所述的1/4球的几何模型;

图1 1/4金属球几何模型
2)材料属性:实心球为铜,金属罩为铜,中间为空气;
3)源与边界条件设定:该题为带金属罩的金属球,中间为自由空间,源为电压源且电位为100V,设定如图2所示。同时,因几何模型对应金属球的1/4,为还原整个球,在几何模型的左边界及下边界应设定为偶对称。模型的上边界及右边界设定为球边界,且无穷远电位为零;
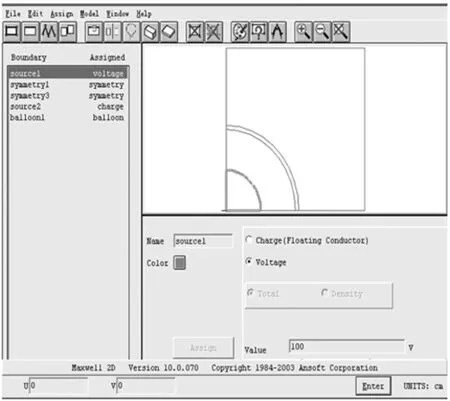
图2 设定电压源
4)进行求解;
5)解后处理:绘出的电位线如图3所示。图3曲线首先验证了等势线沿径向衰减,同时可看出恒定电位的导体球空间电势变化满足球状分布,且源激发的电场在金属罩外呈现相同的变化规律,与理论一致。可沿径向线画出更清晰的电位变化规律,如图4所示。其中横轴单位为cm,纵轴单位为V。
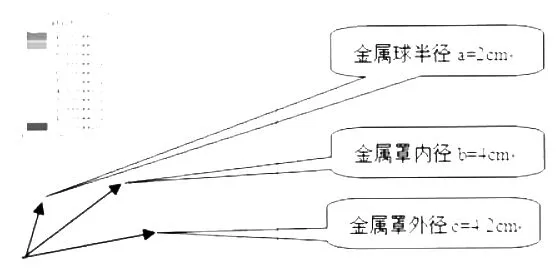
图3 空间电位线

图4 沿径向电位变化规律
由图4可看出金属球为等势体,金属罩为等势体(软件特点:等电位的点被拉到零),球内及金属罩内电场为零,满足静电平衡的结论,且在球与罩之间及金属罩外空间满足相同的变化规律,说明金属罩并没有阻挡掉内部源向外释放的电场能。
我们可沿径向线画出电场变化规律,如图5所示,其中横轴单位为cm,纵轴单位为V/m。
由图4可知,金属球内及表面为等电位,且在金属球与罩内空间分界面满足电位连续;图5可看出,金属球内及罩内电场为0,且球与罩内空间及外界空间分界面电场不连续。
若要达到完全屏蔽的目的,需要金属罩接地,接地后的等势线分布如图6所示。图中曲线同样得到电场线与等势线衰减之间的变化关系,同时可看出恒定电位的导体球空间电势变化满足球状分布,且源激发的电场在金属罩外无分布,验证了金属罩的屏蔽作用。
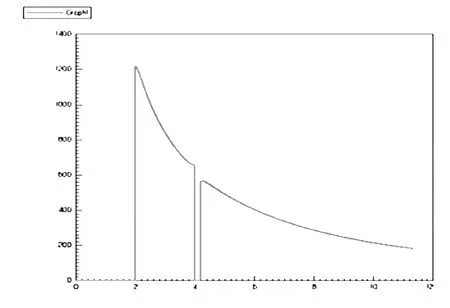
图5 沿径向电场变化规律

图6 金属罩接地后的电位线
我们可沿径向对角线画出电位变化规律,如图7(a)所示。其中横轴单位为cm,纵轴单位为V。由图可见,金属球为等势体,金属罩为等势体,球内及金属罩内电场为零,满足静电平衡的结论,且在球与罩之间满足球状分布的变化规律,金属罩外电位为零,电场为零,说明无电场,接地金属罩达到内外完全屏蔽的目的[6]。同时,可沿径向线画出电场变化规律,如图7(b)所示。其中横轴单位为cm,纵轴单位为V/m。

图7 金属罩接地后沿径向的电位和电场变化规律
通过上述实例,学生可以观察到静电屏蔽下场的分布规律,增加对场的感性认识,更深刻体会到电磁场理论在实际生活中的应用。比如,联系防辐射服的屏蔽作用。
3 金属罩不闭合特性
一种防辐射服好比不闭合的金属空腔,专特定模型下(点电荷源)非闭合空腔对电位与电场线的分布影响,如图8所示。
由图可知,电位线的变化有几乎沿径向衰减的趋势,且空腔内有电场,更清晰的,沿径向线画出电场变化规律,如图9所示。图中横轴单位为cm,纵轴单位为V/m。可看出空腔分散导致电场线进入空腔,空腔未起到完全屏蔽作用。

图8 非闭合空腔的电位和电场分布
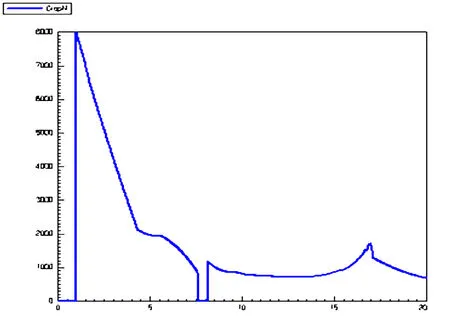
图9 沿径向电场变化规律
4 结语
“电磁场与电磁波”教学中引入Ansoft电磁场分析软件具有一定的意义。我们基于Maxwell 2D通过金属罩对内部空间的屏蔽实例,与理论对照可看出Ansoft的正确与形象。同时,对场的空间描绘可增加学生对场的感性认识,加深他们对电磁场理论及其应用的理解,激发对电磁场的学习兴趣,培养其解决实际工程问题的能力,提高教学效果。
[1] 赵彦珍,应柏青.Ansoft在“电磁场与波”课程教学中的应用[J].南京:电气电子教学学报,2010,32(2):95 ~96
[2] 陈执平.本科电磁场教学中引入ANSYS的尝试[J].北京;大学物理.2009,29(7):32 -35
[3] 胡盘新,钟季康.在大学物理教材中引入计算机数值解的尝试[J].北京:物理与工程,2006,16(2):47-50
[4] Jian Wang,LiDong Liu,YouHua Gao,ect.Study on numerical simulation of electrical fields inside isolated phase bus based on ANSOFT[J].Electrical Machines and Systems,2008,(8):17 -20
[5] 刘国强,赵凌志,蒋继娅等.Ansoft工程电磁场有限元分析[M].北京:电子工业出版社,2006
[6] 冯慈璋,马西奎.工程电磁场导论[M].北京:高等教育出版社,2000
