涪陵青草背长江大桥主缆无应力长度计算

胡 娜，张永水，成宁波

(1.重庆交通大学土木建筑学院，重庆400074;2.重庆建工市政交通工程有限责任公司，重庆400021)

悬索桥是大跨度桥梁中最具竞争力的桥型之一。对桥梁结构的施工过程进行合理的施工控制是使桥梁施工过程和成桥状态与设计要求尽可能接近的重要保证，是增加结构施工安全性的一个重要手段［1］。对悬索桥施工控制的首要任务则是确定主缆的无应力长度［2］。

利用大型有限元软件Midas/Civil建立悬索桥的分析模型，通过成桥状态主缆线形可快速的得出悬索桥的主缆无应力长度［3］。但在实际工程中，主缆塔顶IP点和边缆锚固端IP点之间的索股无应力长度并非下料时的参考值，而是取主索鞍和散索鞍的圆弧切点(即TP点)之间的圆弧段长度［4-5］。因此，必须对软件计算得到的悬索桥主缆无应力长度进行修正，进而为施工控制提供依据。

1 工程概况

涪陵青草背长江大桥为单跨788 m悬索桥。车辆荷载采用公路-I级，桥梁全宽27.5 m，主缆中心距28.7 m。主缆由5跨组成，由北向南分别为:南锚跨、南边跨、中跨、北边跨、北锚跨。其跨径组成为18.867 m+245 m+788 m+245 m+17.831 m。两根主缆中各含88股平行钢丝索股，竖向排列成尖顶的近似正六边形。加劲梁为流线型扁平钢箱梁，正交异形板桥面，索塔采用混凝土门形框架式，基础均为钻孔群桩。主桥立面图布置见图1。

2 精确的初始平衡状态分析

Midas/Civil建立悬索桥模型首先需要做自重荷载作用下的初始平衡状态分析。所谓初始平衡状态即是悬索桥在加劲梁的自重作用下产生变形后达到平衡状态;而在满足设计要求的垂度和跨径条件下，计算主缆的坐标和张力的分析则称为初始平衡状态分析［6］。该软件首先采用悬索桥的基本假定，利用节线法确定悬索桥的初始线形，再以初始线形为基础，采用悬链线索单元做更精确的分析，即采用悬索桥分析控制功能进行精确平衡状态分析。

图1 涪陵青草背长江大桥立面Fig.1 Section layout of Fuling Qingcaobei Yangtze River Bridge

采用该软件，建立了涪陵青草背长江大桥的三维空间有限元模型，共427个节点，420个单元。首先通过悬索桥建模助手输入该桥的基本信息，得到初始的平衡状态。根据图纸资料，计算桥面系的净重、拟定主缆和吊索的直径D和截面积A，在保证重量不变的前提下，修正主缆和吊索的容重r，其计算参数如表1。

表1 涪陵青草背长江大桥建模参数(基准温度20℃)Tab.1 Model parameters of Fuling Qingcaobei Yangtze River Bridge(fiducial temperature 20℃)

为了得到与真实受力状况一致的悬索桥分析模型，需修改模型的部分特性，以使有限元模型与实际吻合。该模型需要作修改的部分如下:

1)加劲梁与吊索的连接方式。根据实际情况，加劲梁和吊索的连接方式采用刚性连接，以加劲梁中心为主节点，前后索面两吊索与加劲梁连接点为从节点，使吊索和加劲梁连接点的自由度从属于同一x-z平面加劲梁中心处的节点。

2)支座模拟。加劲梁梁端放置在支座上，而支座设置在桥塔横梁上，故在连接处应模拟实际支座受力。此处采用一般弹性连接方式，刚度值根据实际给出的支座品种和规格确定。

3)主索鞍模拟。塔顶处主索鞍采用刚性连接实现主从约束。

4)静力荷载工况类型。静力荷载工况应由单元的自重、二期恒载、索夹、吊杆处的锚头和检修道立柱组成，为便于分析，将上述荷载均放到同一个荷载工况中。

采用悬索桥分析控制功能，对初始平衡状态得到的模型进行必要的修改之后，进行悬索桥精确平衡状态分析，直到收敛误差在允许范围之内，且主缆无应力长度变化趋于稳定为止。程序将提供几何刚度初始荷载和平衡单元节点内力，以及主缆各个节点的张力、主缆的无应力长度和主缆在索鞍处的水平夹角，如图2、表2和表3(修正前)。

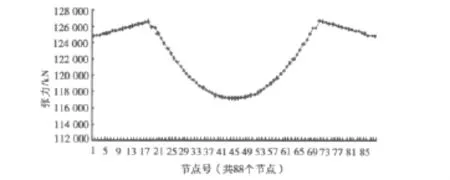
图2 主缆各个节点的张力值Fig.2 Tensile force of each point for main cable

表2 成桥状态主索鞍与散索鞍处主缆与水平方向的夹角Tab.2 Horizontal intersection angles between main cable saddle and free cable saddle

表3 修正前后中心索股无应力长度Tab.3 Zero-stress length value of central strand before and after rectification /m

3 主缆无应力长度修正

显然，由表3(修正前)可得经过精确平衡分析后的主缆边跨，中跨的无应力长度。这时需对各段中心索股无应力长度进行修正，进而通过索股间几何关系，确定各根索股的无应力长度。笔者只考虑中心索股的修正，即指鞍槽底部向上偏移一个主缆半径值的纵向曲线。

主缆的无应力长度即是主缆在自由悬挂状态下的长度，也就是常说的下料长度。成桥状态时主缆在自重及各种荷载作用下达到平衡状态，这时主缆的长度为有应力长度，即是无应力长度与弹性伸长之和［7］。弹性伸长的公式采用 ΔL=FL/EA求得。其中，ΔL为弹性伸长，F为主缆的张力，L为主缆的应力长度，E为弹性模量，A为主缆的面积。

3.1 主索鞍处主缆无应力长度修正

由模型知，主缆水平力处处相等，均为117 179.2 kN。从图2可以得到在主索鞍朝边跨向和朝中跨向张力分别为Fb=126 682.7 kN和Fz=125 932.7 kN(70、71号单元);在散索鞍朝边跨向为 Fsb=124 896.1 kN(88号单元)。主缆的理论交点和实际交点偏离量为Δ=49.2 mm，由图3知，通过圆弧中心半径为R=6 000 mm的圆与中跨、边跨相切并交于TP点。可以看到，主缆的实际路径应该为图中所示虚线，理论交点(IP点)的大样如图4。

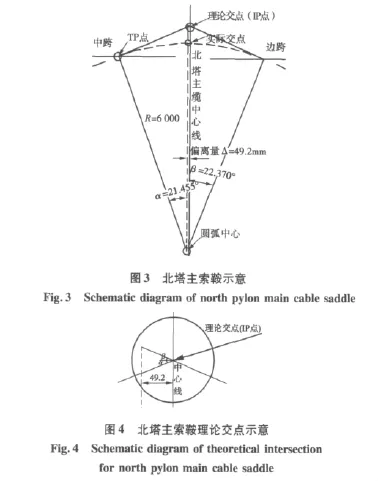
得到主索鞍处中跨主缆的无应力长度修正公式:

同理可得到主索鞍处边跨主缆的无应力长度修正公式:

式中:L表示TP点到理论交点IP点的长度，Lz指中跨，Lb指边跨;Sz、Sb分别指中跨和边跨在主索鞍处修正后的无应力长度;Tz、Tb分别指中跨和边跨经软件计算的无应力长度;ΔLz、ΔLb指中跨和边跨修正索段的弹性伸长，其计算公式如下:

3.2 散索鞍处主缆无应力长度修正

本文散索鞍处的修正只针对边跨部分，仍然以北边跨为修正对象，对散索鞍处北边跨无应力长度的修正公式如下:

其中:l是指TP点到IP点的距离;Δl为l的弹性伸长，Δl=Fsb·l/EA;γ为起弯面与散索鞍中心线的夹角，γ=θ-β;D指索槽底部到缆索中心线的距离，已知D=324.5 mm;Ssb'指边跨Sb经散索鞍处修正之后的无应力长度;北散索鞍起弯面与第1段圆弧半径交点示意见图6。

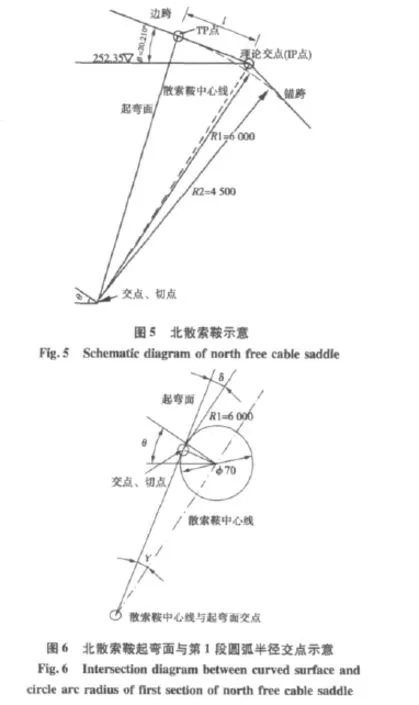
将表2、表3(修正前)所得中跨无应力长度值和索鞍与水平向的夹角值代入公式(1)～公式(3)，可以得到 Lz=2.411 m，Sz=806.202 m，Lb=2.416 m，Sb=262.205 m。

将北散索鞍处主缆与水平方向的夹角θ值(北散索鞍为 32.438 5°，南散索鞍为 30.598°)代入公式(4)，得到 l=1.406 m，S'sb=260.804 m。同理可得南边跨修正后的无应力长度值，如表3所示(修正后)。

3.3 锚跨索股的无应力长度计算

由文献［8］得，锚跨处的索股的无应力长度需要单独计算。散索鞍是一个由几段半径不同的圆弧连成，且具有平弯的复杂空间体。索股平行地进入散索鞍后，分散成彼此独立的既有平弯又有竖弯的复杂的空间曲线，顺着不同的槽路散开，并沿着不同的方向交于锚固面上［8］。本桥中的锚跨采用编制程序计算所得，该程序具有很高的精度，在此不再赘述，计算所得值如表3(修正后)。

4 结论

1)笔者采用通用软件Mdias/Civil建立悬索桥模型，建模之前的前期准备工作是建立模型准确与否的关键，悬索桥的一期、二期恒载对主缆的无应力长度的确定起关键作用。因此在悬索桥建模助手中除加劲梁上的临时荷载不考虑在桥面系荷载中，成桥之后作用在桥上的永久性荷载都要包括其中。

2)Mdias/Civil采用建模助手建立悬索桥的初始平衡状态是为得到主缆的初始线形，在实际建模过程中，要充分考虑实际工程的具体连接方式，受力特性等，进而在初始平衡状态下对模型做必要的修改，得到精确平衡分析状态。

3)采用通用软件得到的主缆无应力长度经修正后的结果正确，误差在允许范围内。说明利用通用软件建模得到的数据是可信的，须经过上述方法修正后方可在下料时采用。本文为悬索桥使用通用软件计算主缆无应力长度提供了参考。

［1］顾安邦，张永水.桥梁施工监测与控制［M］.北京:机械工业出版社，2005.

［2］雷俊卿.悬索桥设计［M］.北京:人民交通出版社，2004.

［3］罗喜恒，肖汝诚，项海帆.空间缆索悬索桥的主缆形分［J］.同济大学学报:自然科学版，2004，32(10):1349-1354.LUO Xi-heng，XIAO Ru-cheng，XIANG Hai-fan.Cable shape analysis of suspension bridge with spatial cables［J］.Journal of Tongji University:Natural Science，2004，32(10):1349-1354.

［4］梅秀道，汪正兴，秦建刚，等.悬索桥索股下料长度求解方法及其影响因素分析［J］.工程设计学报，2008，15(4):308-312.MEI Xiu-dao，WANG Zheng-xing，QIN Jian-gang，et al.Method and impacting factors analysis in computing fabrication length of suspension bridge’s main cable strand［J］.Journal of Engineering Design，2008，15(4):308-312.

［5］李小珍，强士中.悬索桥主缆空缆状态的线形分析［J］.重庆交通学院学报，1999，18(3):7-13.LI Xiao-zhen，QIANG Shi-zhong.Geometric form analysis of suspension bridge free cable［J］.Journal of Chongqing Jiaotong University，1999，18(3):7-13.

［6］北京迈达斯技术有限公司.Midas/Civil悬索桥分析功能使用说明［M］.北京:北京迈达斯技术有限公司，2006.

［7］黄平明，梅葵花，徐 岳.大跨径悬索桥主缆系统施工控制计算［J］.西安公路交通大学学报，2000，20(4):19-28.HUANG Ping-ming，MEI Kui-hua，XU Yue.The calculation method of main cable system construction control of long-span suspension bridge［J］.Journal of Xi’an Highway University，2000，20(4):19-28.

［8］谭红梅，肖汝诚.悬索桥主缆索股无应力索长计算分析［C］∥第十六届全国桥梁学术会议论文集.北京:人民交通出版社，2004.