斜拉桥稳定性分析的主梁有限元模型探讨

黄智华，邓平跃，张大伟，张 鹏

(1.上海浦东建筑设计研究院有限公司，上海201204;2.西南交通大学 土木工程学院，四川成都 610031)

随着斜拉桥跨度的不断增大，稳定安全性越来越突出。预应力混凝土斜拉桥大量采用悬臂施工，充分利用了斜拉索的竖向分力，使得斜拉桥的主梁弯矩减小，可以做得较为纤细。但是由于主梁和塔都承受较大的压力，因此有必要对其施工阶段进行稳定分析。

针对重庆地维长江公路大桥，在施工到最大双悬臂时结构的整体稳定性进行分析。该桥跨径组合为141 m+345 m+141 m，双塔双索面漂浮体系预应力混凝土斜拉桥。主梁采用双主肋结构形式，梁高1.9 m，宽为15 m，如图1。横隔板间距一般为8 m。索塔采用墩塔固接型式，斜拉索在主梁上锚固于梁肋中间。本文取该最大双选臂状态分析。这时，两个悬臂长度均为107 m，塔中横梁有临时支座支承主梁梁肋。

图1 主梁截面Fig.1 Sectional view of the main girder

结构问题的研究现在主要分为3种方法，即传统的理论分析、结构实验、及计算力学 方法。有限元作为一种计算力学方法，已经在结构计算中取得了很大的成功。笔者应用有限元软件ANSYS计算结构的特征值稳定安全系数。在结构达到随遇平衡状态时，节点位移矩阵由{δ}变为{δ}+{Δδ}，结构平衡方程也能满足，这时有［1］:

式中:［KD］为结构总体弹性刚度矩阵;［KG］为结构总体几何刚度矩阵;λ为结构稳定安全系数。

这就是结构稳定计算的安全系数的特征方程式。分析该方程，λ与［KD］和［KG］有关。［KG］除了与构件几何特征有关外，还与初始轴力N有关，也就是与结构受力有关。［KD］就只与结构刚度有关。因此，在有限元计算中，如何模拟好结构的刚度，是至关重要的问题。笔者通过考察结构在荷载作用下的特征值计算结果，来分析模型对于其刚度的模拟特点。工程问题一般考虑结构的最低阶的特征值才有意义，同时由于在某种荷载作用下，容易激发结构某种刚度弱点而先发生相应屈曲。因此为了讨论问题方便和有针对性，选取相同荷载作用下，各主要屈曲形态的最低阶特征值作为分析对象。这些主要屈曲形态包括主塔1阶屈曲，主梁1阶竖向弯曲屈曲，主梁1阶扭转屈曲。特别是后面2种模态，与主梁刚度密切相关，因此作为重点考察对象。

1 有限元模型

斜拉桥主梁受到斜拉索的弹性支撑，为了模拟好其刚度已经与斜拉索的连接，一般双索面斜拉桥的主梁梁单元模型主要有单主梁模型、双主梁模型、三主梁模型等［2］。还可以采用更为精确的板壳单元或实体单元模型。实体单元比简化的梁单元模型更符合实际情况，但是，这种模型由于单元数量大，特别是在进行非线性分析时，由于过于消耗机时使得求解变得困难。而使用简化的梁单元模型则能克服这一困难。因此有必要研究使用何种简化模型更能符合结构特性。

对于地维长江大桥的最大双悬臂状态，主塔采用梁单元beam188，该单元建立在Timoshenko梁理论上，考虑了剪切变形，为包括3个平动和3个转动自由度的三维有限应变不带中间节点的梁单元。斜拉索采用只能受拉不能受压的link10单元。陈幼平，等［2］指出，主梁可以离散为单主梁带刚性短悬臂的鱼骨式模型，双主梁模型，用刚性横梁或实际的横梁连接。在斜拉桥稳定分析中，由于结构的稳定性与结构的刚度密切相关。对于主塔和斜索，模型不变，对于主梁通过选取几种不同的模型，比较其特征值屈曲分析结果，即可得出各自刚度模拟的特点。为了使结果便于比较，取重力荷载为实际的16.2倍，这样，特征值稳定安全系数即为得出的结果乘以16.2

1.1 实体单元模型

为了较为准确的模拟结构的刚度，采用实体单元最好分析结构的稳定性，在ANSYS里，选用带中间节点的solid92四面体单元。该单元有10个节点，每个节点有3个方向的平动自由度。由于是四面体单元，能适应形状不太规则网格的划分。带中间节点的单元，由于内部应力不是常量，因此可以较好的适应结构的变化的应力场，用比较少的单元就可以获得较好的成果，但是却带来计算时间的增加［3］。为了获得精度和计算时间的协调，划分了91 000多个单元进行计算。这时结构的单元划分见图2。

图2 主梁采用实体单元时的结构有限元Fig.2 Unit structure of main beam with solid finite element

图3 1阶面内弯曲失稳Fig.3 Plane bending instability of first-tread main beam

经过求解，得出其特征值见表1，其中塔和主梁的1阶特征值分别为1.08和3.79。分别对应塔的面内屈曲和主梁面内屈曲(图3)，主梁扭转屈曲时1阶特征值为4.76(图4)。

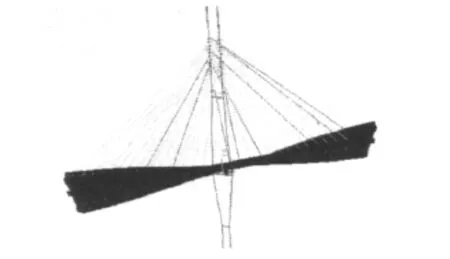
图4 主梁1阶扭转失稳Fig.4 Instability with the first-tread main beam torsion

表1 实体单元特征值计算结果Tab.1 Calculation results of eigenvalue of solid elements

1.2 单主梁模型

单主梁模型是用位于扭转中心的空间梁单元模拟，将主梁的抗弯、抗扭刚度都集中在这组梁单元上，主梁和斜拉索的联系通过主梁伸出的准刚性梁单元的连接来模拟，即为俗称的“鱼骨”模型［2］。项海帆［4］认为这种模型适合于扭转刚度较大的闭口箱梁断面。但在实际中，很多开口截面也采用这种模型，例如，Wilson，等［5］研究的双主肋截面采用的也是这种模型，由于约束扭转等原因，扭转刚度较难模拟。笔者采用beam188单元，带翘曲自由度，包括3个平动和3个转动在内，一共7个自由度，且带中间节点。利用刚度很大的单元来模拟伸出的刚臂。计算结果见表2。

表2 单主梁模型特征值计算结果Tab.2 Calculation results of single-girder model eigenvalue

与实体单元计算结果相比，其大部分特征值结果的特点相似，因此限于篇幅，仅列出主要考察的屈曲模态。塔屈曲1阶特征值相差极小，主梁屈曲1阶特征值为4.22，比实体单元计算结果大11.3%，扭转1阶特征值为8.60，比实体单元计算结果大81%。这表明，对于主梁的竖向刚度，单主梁模型的竖向刚度比实际略大，但在工程上仍能满足要求，对于主梁的扭转刚度，则模拟得过大。

另外，该模型还存在一个特征值为1.28的梁侧向摆动，两塔柱反向纵向弯曲的屈曲模态。这个是较为特殊的，因此选用该模型应较为谨慎，出现这种模态是不正常的。

1.3 双主梁模型，横向刚性连接

双主梁模型，将主梁截面的刚度平均分配在两纵梁上，对于本文的双主肋主梁，一般较为合适［6］，Nazmy，等［7-8］成功的将该模型应用到大跨斜拉桥的非线性地震反应分析中。但是这种模型主要问题在于两纵梁横向连接的模拟，一般有2种方式模拟，即刚性横梁或实际横梁连接［2］。对于这2种方式，分别做了有限元模型。

和单主梁模型一样，采用带翘曲自由度和中间节点的beam188单元模拟。对于其横向刚性连接，和单主梁一样，采用刚度极大的单元模拟。

计算结果列于表3，由于结果和实体单元基本上相似，仅列出主要模态的。可以看出，除了没有单主梁模型多出来的梁塔侧弯模态外，其屈曲模态和特征值和单主梁模型很相近。和实体单元比较，主要屈曲模态是一样的，就不再列出其图。塔面内弯特征值相差极小，主梁1阶面内弯特征值偏大5%，在工程许可的范围内，主梁1阶扭转特征值偏大76.7%，表明和单主梁模型一样，扭转刚度模拟过大。

表3 双主梁刚性横梁特征值计算结果Tab.3 Calculation results of double-girder rigid beam eigenvalue

1.4 双主梁模型，实际横梁连接

将横梁刚度改为实际的，即采用横隔板刚度，这时的计算结果大不相同(表4)。塔面内和梁面内弯两种屈曲模态和实体元相比，相差很小。但是，其弯扭屈曲特征值太小，说明用实际横梁连接，对于扭转刚度模拟是错误的，比实际情况小了很多。从模型上理解，原来是桥面和横隔板共同形成横向连接刚度，但是采用双主梁，忽略了桥面板提供的横向刚度，但是这项刚度非常大，因此这种连接方式不可取。

表4 双主梁实际横梁特征值计算结果Tab.4 Calculation results of the beam eigenvalue of double-girder

1.5 双主梁模型、等效横向连接

上述两种传统的双主梁模型，对于侧弯刚度和扭转刚度模拟不准［2，9］。双主肋混凝土桥，纵向有双主肋，横向有横隔板来支承桥面板，可看作一种梁板结构，因此可以采用梁格理论来分析。该理论将分散在每一区段的弯曲刚度和抗扭刚度集中于最邻近的等效梁格内，实际结构的纵向刚度集中于纵向梁格构件内，而横向刚度则集中于横向梁格构件内。对于梁格有横隔板，且间距不大时［10］:

EIx=E×(T形截面对x轴的惯性矩)

GJx=G×(隔板抗扭惯性矩+bh3/6)

其中:b为梁格代表的板宽;h为板的厚度;bh3/6项是考虑T形截面的翼缘的抗扭惯矩的。一般狭长矩形截面的抗扭刚度为bh3/6，因此建模时可以考虑取实际的隔板宽度的1/2来等效抗扭刚度。

用双主梁模型，由于在考虑横向连接时，刚性横梁连接则放大了刚度，实际横梁连接则缩小了刚度。故根据梁格理论，采用称为等效刚度的横梁来模拟横向连接。该等效横梁是一T梁，翼缘为桥面板，腹板为横隔板，为了用beam188单元计算刚度的方便，翼缘宽度考虑2种情况:一种为横隔板间距b，另一种为b/2。前种方式主要是考虑到抗弯刚度的模拟，后者则是为了抗扭刚度的模拟。读者也可以自己按照上述原理计算抗弯和抗扭刚度。表5列出了塔面内弯、梁面内弯和梁扭转的1阶计算结果。

表5 塔面内弯、梁面内弯和梁扭转的1阶计算结果Tab.5 Calculation results of first-tread eigenvalue of tower bend，beam bend and beam twist

对于翼缘宽度为b的情况，主梁1阶弯曲屈曲特征值比实体单元法的大了1.6%，而主梁1阶扭转特征值则大了4.4%。对于翼缘宽度为b/2的情况，主梁1阶弯曲屈曲特征值则大了1.5%，其1阶扭转特征值则大了4.0%。说明这两种方式对于模拟主梁的刚度是非常合适的。

比较发现，翼缘宽度为b和b/2两种方式区别不大，翼缘宽度为b/2的对于刚度模拟的略小，但是它们都是满足要求的。

因此，在实际空间分析简化计算中，根据梁格理论，采用等效刚度的横向连接是非常可靠的，其刚度介于实际横梁和刚性横梁之间，克服了前者过柔后者过刚的弱点，较为真实的模拟了结构的刚度。其模型比较简便，比实体单元计算量小很多，精度可以达到要求。该方法值得推广。

1.6 壳单元模型

可以采用包括平面变形和板弯曲变形的壳单元来模拟主梁。桥面板和横隔板均较薄，单元选取较为方便。对于主肋，由于高度和宽度均较大，高为1.9 m，标注段肋宽为1.6 m，因此一般薄壳单元已不实用。将肋宽方向取为壳单元厚度方向，这样壳的厚度为1.6 m。选用shell181单元分析，该单元能适应从薄到中厚的板壳单元。且该单元为有限应变壳单元，每个单元有4个节点，每个节点有6个自由度，包括3个平动和3个转动自由度。采用完全积分，这样面内有2×2个积分点。其主要模态计算结果如表6。

表6 壳单元特征值计算结果Tab.6 Calculation results of shell element eigenvalue

和前面几种单元一样，其塔面内弯和实体单元结果相差无几，主梁面内1阶屈曲特征值比实体单元大了7.6%，而主梁1阶扭转屈曲特征值比实体单元小了2.9%。故板壳单元模拟得较好。

2 结语

斜拉桥整体稳定性分析中，采用简化模型可以大大减少计算量，但是也容易由此带来误差甚至错误。笔者分别将几种常用的简化模型与实体单元模型计算结果作对比，并提出了一种新的双主梁模型。主要得出了如下结论:

1)单主梁模型和双主梁刚性横向连接模型对于主梁的竖向抗弯刚度略偏大，能满足工程要求。主要缺点在于对于抗扭刚度模拟过大。

2)双主梁实际横向连接模型是过低地模拟了横向连接，其抗扭刚度的模拟存在很大问题。

3)利用梁格理论，采用等效刚度的横向连接的有限元模型与实体单元模型计算结果差别很小，值得推广使用。特别是在非线性计算中，由于实体单元计算量过大，不得不采用量单元模型时，采用这种模型既节省机时，又能很好的模拟结构刚度分布特性。

［1］李国豪.桥梁结构稳定与振动［M］.修订版.北京:中国铁道出版社，2002:99-101.

［2］陈幼平，周宏业.斜拉桥的动力分析模型［J］.中国铁道学报，1995，16(1):79-83.CHEN You-ping，ZHOU Hong-ye.Modelling of cable-stayed bridges for dynamic analysis［J］.China Railway Society，1995，16(1):79-83.

［3］朱伯芳.有限单元法原理与应用［M］.2版.北京:中国水利水电出版社，1998:92-95.

［4］项海帆.高等桥梁结构理论［M］.北京:人民交通出版社，2001:294-295.

［5］Wilson J C，Graveue W.Modelling of a cable-stayed bridges for computer for dynamic analysis［J］.Earthquake Engineering and Structural Dynamics，1991(2):20-22.

［6］REN Wei-xin，PENG Xue-lin.Baseline finite element modeling of a large span cable-stayed bridge through field ambient vibration test［J］.Computers and Structures，2005，83:536-550.

［7］Nazmy A S，Abdel-Ghaffar A M.Nonlinear earthquake response analysis of long-span cable-stayed bridges:theroy［J］.Earthquake Engineering ＆ Structunal Dynnamics，1990，19(1):45-62.

［8］Nazmy A S，Abdel-Ghaffar A M.Nonlinear earthquake response analysis of long-span cable-stayed bridges:applications［J］.Earthquake Engineering ＆ Structural Dynamics，1990，19(1):63-76.

［9］苏成，韩大建，王乐文.大跨度斜拉桥三维有限元动力模型的建立［J］.华南理工大学学报:自然科学版，1999，27(11):51-56.SU Cheng，HAN Da-jian，WANG Le-wen.The establishment of 3-D finite element dynamic models for long-span cable-stayed bridges［J］.South China University of Technology:Natural Science，1999，27(11):51-56.

［10］戴公连，李德建.桥梁结构空间分析设计方法与应用［M］.北京:人民交通出版社，2001:26-29.