基于贝叶斯网络的城市道路交通事故分析

赵金宝 邓 卫 王 建

(东南大学交通学院，南京 210096)

面对大量的交通事故及安全隐患，国内外在交通事故分析及预测模型上的研究成果多为单因素或多因素统计性回归形式，主要通过系统致因理论来分析交通事故的特点，缺乏对交通事故导致因素之间相互关联的关系进行层次性的系统分析.文献［1］在哈顿矩阵和事件链方法的基础上，提出了基于C3-R3系统的事故分析方法;文献［2］运用系统科学的宏观数据，从驾驶员、步行者、车辆及道路调价和交通管理的角度，分析了交通事故的成因.相关研究着重研究不同因素对事故的影响，但在分析过程中往往假设交通事故的致因变量是相互独立和不相关的，这与实际不相符.交通事故的发生往往是多个因素相互作用的结果，表现出明显的层次性，因此，对不同因素相互关联作用下的交通事故进行分析和预测是十分有必要的.

以变量之间的相互作用为前提、通过参数学习和概率推理来获取结果分布信息的贝叶斯网络已广泛应用于航空系统风险分析［3］、搜索营救可靠性分析［4］以及核工业操作员的环境评价［5］.研究结果表明，贝叶斯网络在概率分析具有强大优势，而利用贝叶斯网络进行城市道路交通事故推理分析和安全诊断研究还为数不多.文献［6］应用结构较简单的Empirical Bays(EB)模型对交通事故数进行预测的结果表明，与广义线性模型相比，EB模型的预测结果更接近实际.贝叶斯网络与回归模型相比，对线性和可加性统计假设没有严格的要求，能够有效处理变量较多且变量之间存在交互作用的情况，也能够从大量复杂的数据中发现知识和结构.因此，本文将建立城市交通事故分析的贝叶斯网络模型，以探索贝叶斯网络在城市交通事故分析预测中的应用.

1 贝叶斯网络

贝叶斯网络的拓扑结构为有向无环图(DAG)，用条件概率表达关系强度.在实际应用中，贝叶斯网络主要完成结构学习、参数学习和推理分析3个方面的任务.

1.1 结构学习

贝叶斯网络结构构建包括3种方法:①基于专家认识、根据先验知识确定贝叶斯网的变量节点，进而确定贝叶斯网络的结构;②通过对样本数据的学习，由机器算法自动获取贝叶斯网络结构;③基于专家知识和对数据的机器学习，通过数据融合的方法获得贝叶斯网络结构.文献［7］对贝叶斯网络模型在环境工程领域应用的统计分析结果表明，基于专家知识和机器学习的数据融合方法来确定贝叶斯网络结构的比例达到了43.9%，由于第3种方法综合了专家知识和机器学习2方面的优势，同时可以避免仅使用一种方法确定贝叶斯网络结构的弊端.因此，本文采用第3种方法确定城市道路交通事故分析的贝叶斯网络结构.其中机器学习采用K2算法［8］，K2算法在Matlab中的实现过程如下:

Input:ordering，database+metric;

Output:net struture.

for i=1 to n do

πi=∅

p_old=g(i，πi)

do

z=argmaxkg(i，πi∪{k})where z∈pred(i)

p_new=g(i，πi∪{z})

if p_new＞p_old then

p_old=p_new

πi=πi∪z

else

ok_to_proceed=false

end if

end while

end for

从K2算法的实现过程可以发现，K2算法为贪婪式算法，并不能保证得出的网络为最优网络，需要融合专家知识以得到最优网络结构.

1.2 参数学习

给定贝叶斯网络拓扑结构后，可进行贝叶斯网络的参数学习.有2种常用的参数学习方法来确定各节点变量的条件概率分布:最大似然估计MLE法和贝叶斯法.其中贝叶斯法的基本思想是:给定一个含有未知参数的分布以及一个完整的实例数据集合c，θ为具有先验分布p(θ)的随机变量.参数θ在数据集合c下的条件概率表示为称为参数θ的后验概率.贝叶斯参数学习的任务就是计算这个后验概率.p(θ)通常采用Dirichlet分布［9-10］，这是因为Dirichlet分布的共轭特性可以降低计算的复杂程度，提高计算效率.p(θ)的Dirichlet分布形式为

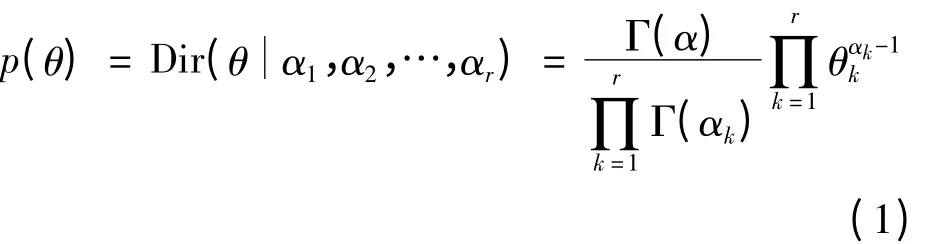
样本发生的概率为

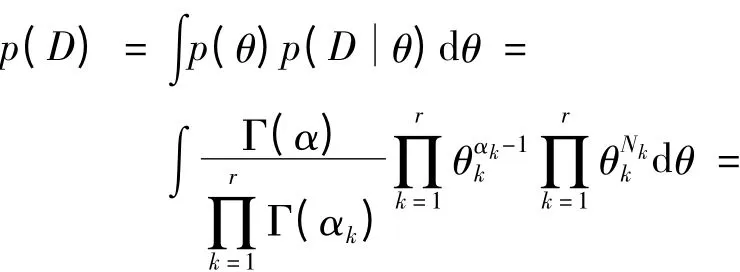
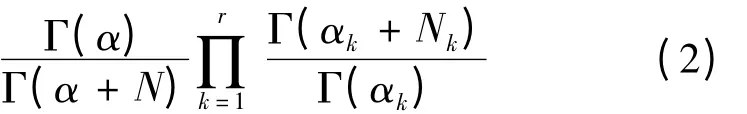
参数θ的后验分布为

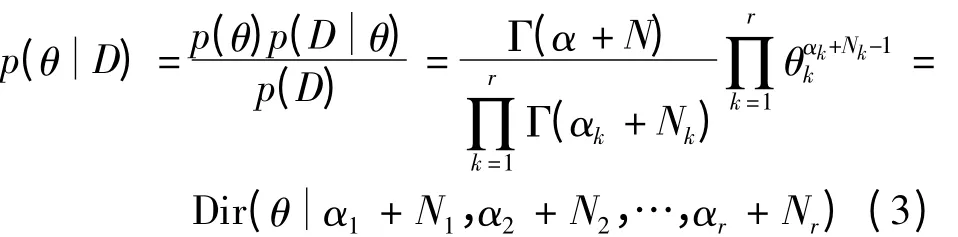
1.3 推理分析

利用建立的贝叶斯网络进行推理分析，是贝叶斯网络要解决的主要任务之一.贝叶斯网络的DAG图形模式给出了所有变量的一个完整的联合概率分布，其推理过程意味着在给定一组证据变量(原因)确切值的情况下，计算一组查询变量(结果)的概率分布.

目前贝叶斯网络的推理方法大致可以分为准确推理和近似推理.贝叶斯网络准确的概率推导是一个NP-hard问题［11］.实际应用中常选择有效的算法进行近似推理，以牺牲推导结果的精确度来换取推导效率的提高.常用的推理算法有联合树算法、消元法、全局推断法等，其中，联合树算法［12-14］应用最为广泛.由于该算法的相关研究已经比较成熟，且在Matlab中可以直接调用该算法，因此本文中不再详细说明其理论计算过程.

2 贝叶斯网络学习结果

2.1 变量选择和数据预处理

应用江苏省常熟市2010—2011年28条主要道路交通的事故资料，经数据整理后，得到由5 190起事故数据组成的样本数据训练集.该事故资料中的各种变量达到10多种，筛选出8个变量，即天气情况、照明条件、事故时间、环境条件、车辆类型、事故地点、交通参与者和事故类型进行城市道路交通事故贝叶斯网络的结构学习和参数学习.

贝叶斯网络可以处理连续变量和离散变量.由于交通事故变量的分类结果有明显的离散性，因此采用离散变量进行城市道路交通事故的贝叶斯网络分析.在进行学习和推理前，首先要对城市道路交通事故各种变量进行离散化处理，经处理后得到的各变量的分类描述和离散化取值如表1所示.

表1 城市道路交通事故变量的分类描述及离散化结果

2.2 贝叶斯网络结构学习结果

本文采用专家知识和K2算法相融合的方法获得贝叶斯网络结构，以样本数据集为基础，利用专家知识确定城市道路交通事故各变量的节点全序，应用K2算法在Matlab的bnt工具箱中完成程序编程，进行城市道路交通事故分析贝叶斯网络结构学习，学习结果如图1所示.

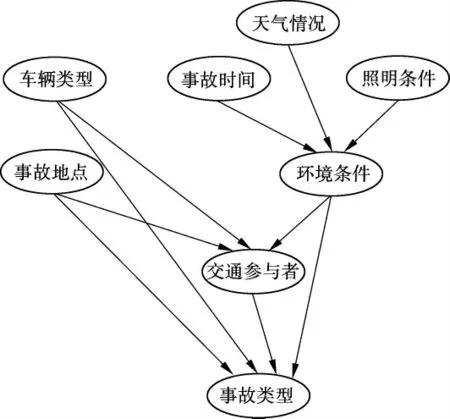
图1 城市道路交通事故分析的贝叶斯网络结构

图1所示的城市道路交通事故分析贝叶斯网络由8个节点和若干连线组成，8个节点为表1中对应的8个变量，节点之间的连线表明变量间的相互影响关系.由图1可以看出，城市道路交通事故的某些变量呈现出明显的影响和被影响的层次关系.交通事故是人-车-路-环境各个变量相互作用的产物，这在城市道路交通事故的贝叶斯网络结构中得到了充分的体现，如交通参与者受环境条件、车辆类型和事故地点的影响，同时又影响交通事故的类型;车辆类型在影响交通参与者的同时又影响交通事故的类型.贝叶斯网络所呈现出的变量之间的相互影响的层次关系充分反应了城市道路交通事故的实际情况.

2.3 贝叶斯网络参数学习结果

贝叶斯网络结构形成后，可以对贝叶斯网络中的各种变量进行参数的学习.表2列出了交通参与者在事故地点、环境条件和车辆类型共同作用下的参数学习结果(后验概率分布).由于数据量较多，本文仅列出了事故地点离散化取值为1(普通路段)的交通参与者的参数学习结果.由表2可以看出，在3种因素共同作用下，交通参与者的违法违规的后验概率最大，其平均值为0.291 1，为其他分类平均后验概率的2倍以上.表2中设Di(事故地点-环境条件-车辆类型-交通参与者)为特定数据点，则D1(1-1-2-5)=0.227 8，D2(1-1-4-3)=0.070 9，D3(1-1-6-1)=0.238 0，D4(1-2-1-6)=0.010 9，D5(1-2-3-4)=0.008 7，D6(1-2-5-2)=0.290 1，D7(1-2-6-7)=0.142 9.

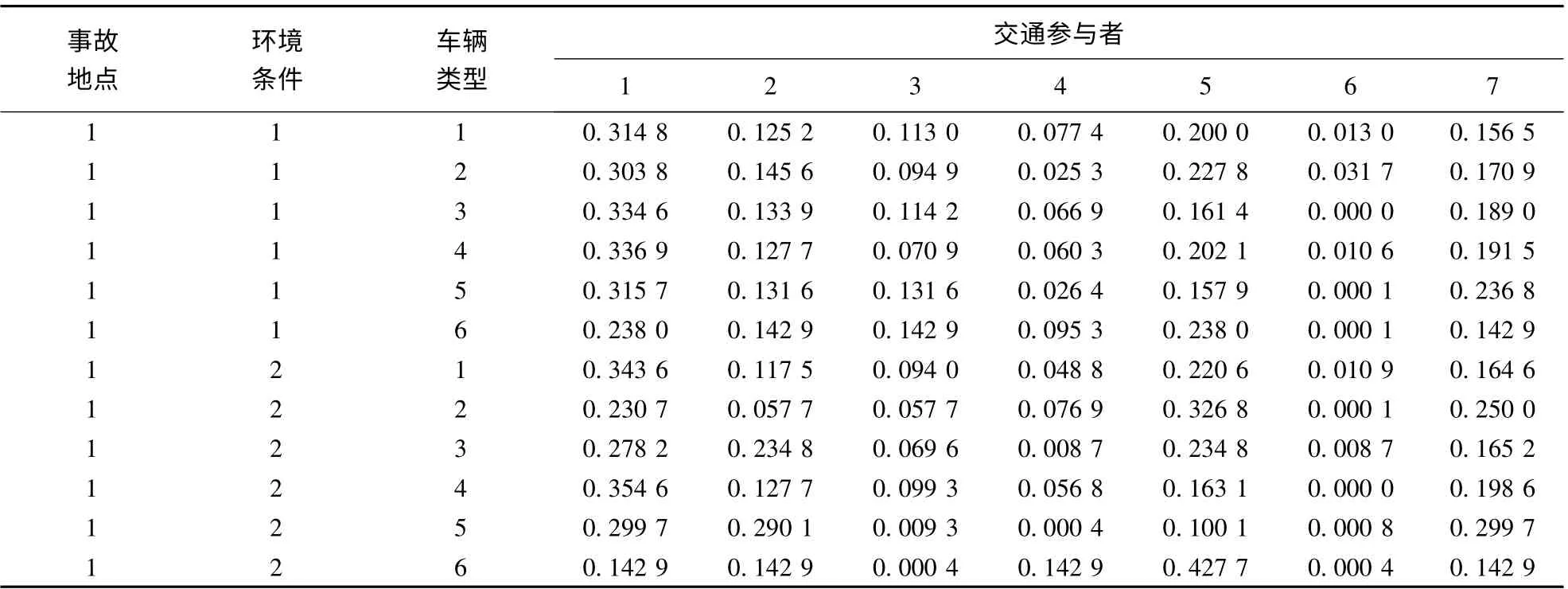
表2 交通参与者的参数学习结果

为验证城市道路交通事故分析贝叶斯网络模型参数学习的精度，本文将贝叶斯网络得到的后验概率与实际计算结果进行了对比分析.表3列出在事故地点(普通路段)、环境条件和车辆类型的共同作用下，交通参与者概率分布的实际计算结果.

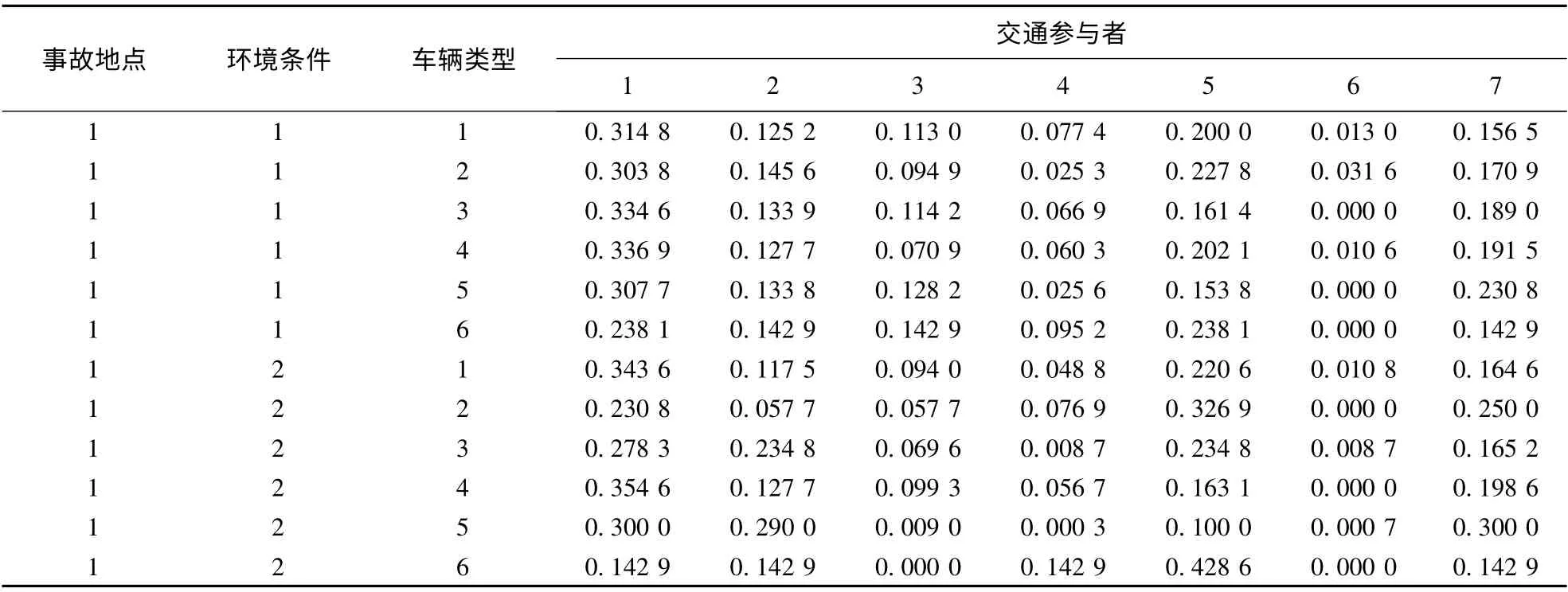
表3 交通参与者的实际计算结果

通过贝叶斯网络模型预测结果和实际计算结果的对比分析发现，由贝叶斯网络得出的后验概率的最大绝对误差为0.008(见图2).与其他预测模型相比［15］，贝叶斯网络模型具有很高的精确度，因此应用贝叶斯网络对交通事故的各个变量进行数据分析和结果预测是可行的.

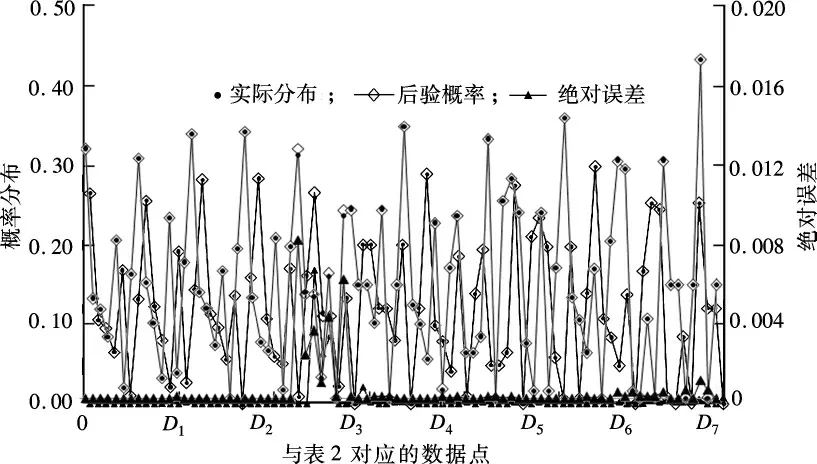
图2 贝叶斯网络参数学习结果的绝对误差分布

3 城市交通事故的推理分析

利用联合树算法对城市道路交通事故进行贝叶斯网络的推理分析.表4列出了车辆类型、事故地点和交通参与者对交通事故类型的推理结果.

根据表4推理结果，具体分析车辆类型、道路地点和交通参与者对城市道路交通事故类型的影响.

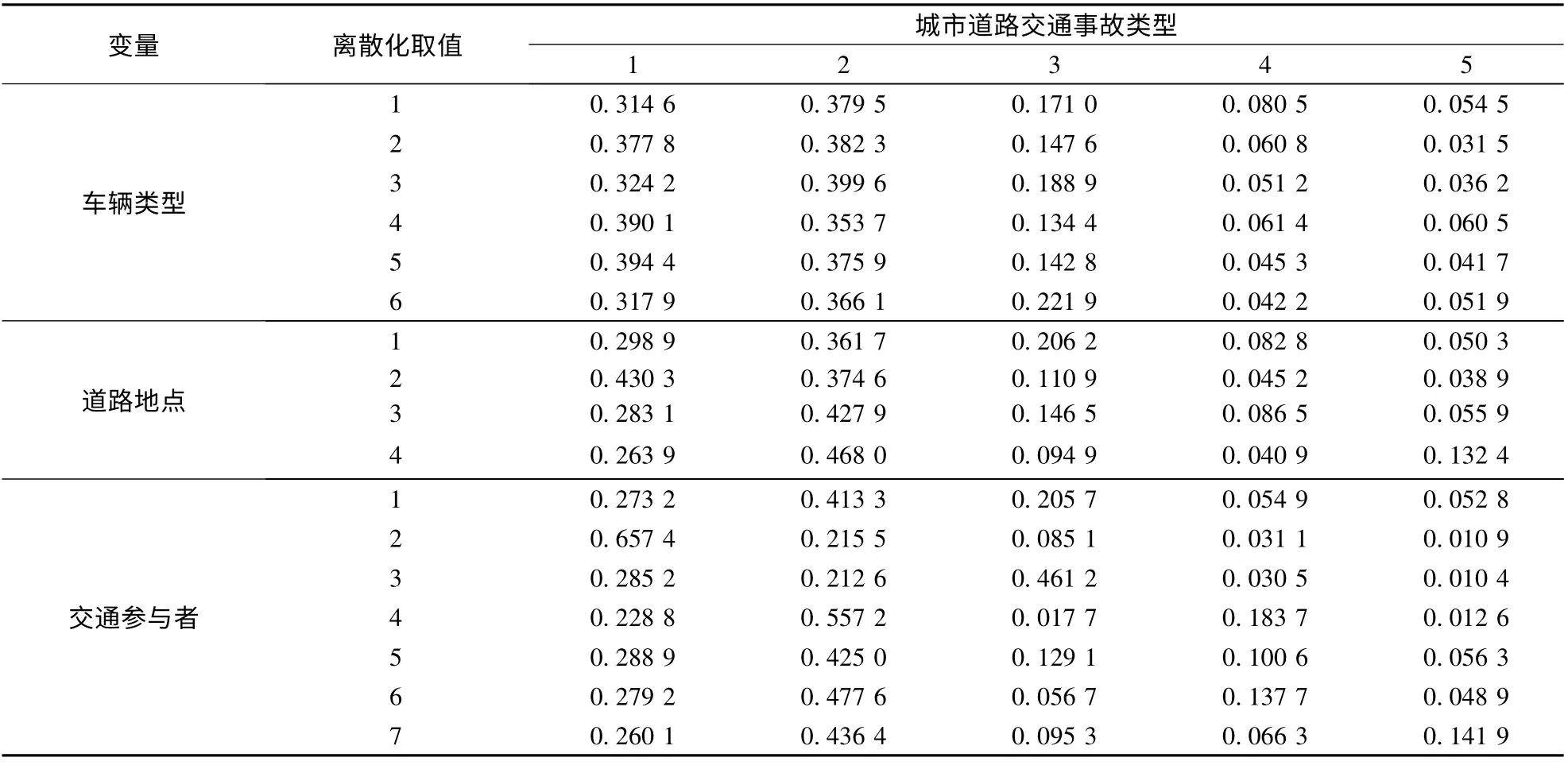
表4 车辆类型、道路地点和交通参与者对交通事故类型的推理结果

3.1 车辆类型对事故类型的影响

根据建立的城市道路交通事故分析的贝叶斯网络模型和推理结果，可以得出不同车辆类型下的城市交通事故类型的概率分布(见图3).

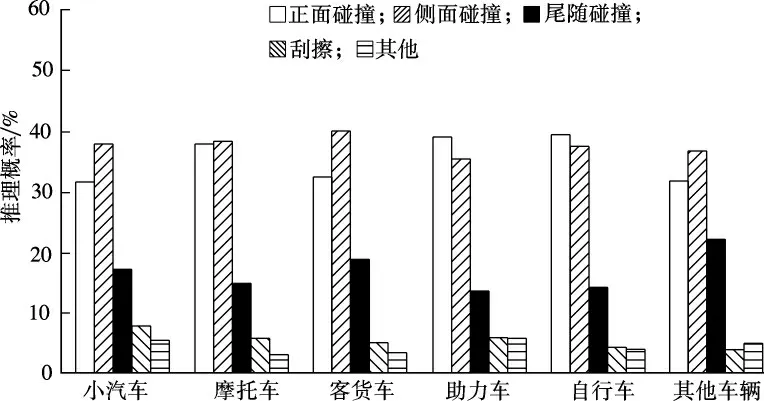
图3 车辆类型对事故类型的影响

由图3可知，对于正面碰撞交通事故，由助力车和自行车等非机动车产生的概率较大，其推理概率分别为39.01%和39.44%，高于其他车型.非机动车运行时的动能和动量较小，正面碰撞是这类车发生事故的主要原因;同时非机动车在城市道路的普通路段和交叉口存在很多逆行行为，也很容易导致正面碰撞事故的发生.客货车等大型车更易发生侧面碰撞，其推理概率为39.96%.由于视线等原因，客货车驾驶员对正面观察较清楚，但对侧面观察不足，易导致侧面碰撞事故的发生.

3.2 道路地点对事故类型的影响

不同道路地点的城市道路交通事故类型的推理概率如图4所示.

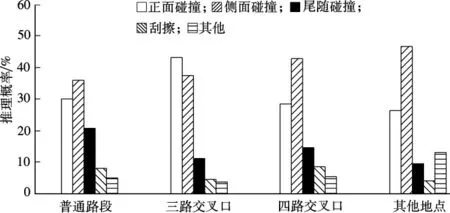
图4 道路地点对事故类型的影响

由图4可知，对于正面碰撞交通事故，在各种地点中三路交叉口发生的概率最高，其推理结果为43.03%.侧面碰撞的概率随着进口道和出口道数量的增加而增加;但普通路段发生尾随碰撞概率较大，其推理结果为20.62%，高于其他事故地点的尾随碰撞的推理概率.

3.3 交通参与者对事故类型的影响

由建立的城市道路交通事故分析的贝叶斯网络模型和推理结果，可以得出交通参与者影响下的城市道路交通事故类型的推理概率(见图5).

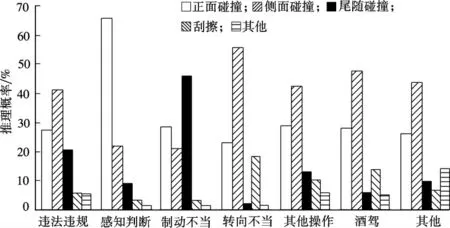
图5 交通参与者对事故类型的影响

由图5可知，正面碰撞事故中，由驾驶员的感知判断失误而引起的概率最大，其推理概率为41.33%.驾驶员的感知判断主要受外界因素的影响，这说明可以通过在路段设置人性化的警告标志以及在交叉口设置合理的渠化设施等可以减少这类事故的发生.侧面碰撞事故中，由于驾驶员的转向不当而引起事故的概率最大，其推理概率为55.72%;转向不当同时也容易引起刮擦事故的发生.驾驶员制动措施不当最易导致尾随碰撞事故的发生，其推理概率为46.12%.

4 结论

1)交通事故的发生是人-车-路-环境相互作用的结果，各变量间表现出明显的影响和被影响的层次性关系.贝叶斯网络的有向无环图形式具有形象直观的表达形式，更接近人的思维特征和推理方式.得到的城市道路交通事故的贝叶斯网络结构学习结果，充分体现了事故变量间的层次性关系，能够对城市道路交通事故的特点进行很好的预测分析.

2)贝叶斯网络参数学习结果表明，贝叶斯网络的后验概率结果具有很高的精确度.与传统事故预测分析模型相比，贝叶斯网络模型具有更高的结果可靠性，通过对预测分析结果的系统分析，可以为制定合理的城市道路交通管理策略、提高城市道路交通安全水平提供更加可靠的理论依据.

3)贝叶斯网络推理结果表明，由于逆行和其自身动能、动量较小等方面的原因，正面碰撞是非机动车发生交通事故主要的类型，但客货车等大型车辆更易发生侧面碰撞事故，且侧面碰撞交通事故发生的概率会随着进口道和出口道数量的增加而增加.交通参与者感知判断失误最易引起正面碰撞事故的发生，由于转向操作不当引起的侧面碰撞事故的概率最大，而制动不当则最易引起尾随碰撞事故的发生.研究分析结果可以为城市道路管理部门深入了解交通事故诱发因素提供理论支持，并为提高城市道路交通系统安全性能提供决策依据.

4)城市道路交通事故是人-车-路-环境复杂巨系统的产物，由于研究时间的限制，更全面更系统的研究有待于进一步地展开，如考虑城市道路交通的管理因素和交叉口处不同的交通控制方式对城市交通事故的影响、更合理有效的贝叶斯网络结构学习、参数学习和概率推理算法的研究等.

References)

［1］Sany R Z，Francis P D N.Improving traffic safety:a new systems approach，1830［R］.Washington DC:Transportation Research Board of the National Academies，2003.

［2］郑安文.我国高速公路交通事故的基本特点与预防对策［J］.公路交通科技，2002，19(4):109-112.

Zheng Anwen.Basic characteristic and prevention measures of motorway traffic accident in China［J］.Journal of Highway and Transportation Research and Development，2002，19(4):109-112.(in Chinese)

［3］Luxhoj J T.Probabilistic causal analysis for system safety risk assessments in commercial air transport［C］//Workshop on Investigating and Reporting of Incidents and Accidents.Williamsburg，VA，USA，2003:17-38.

［4］Norrington L，Quigley J，Russell A，et a1.Modeling the reliability of search and rescue operations with Bayesian belief networks［J］.Reliability Engineering and System Safety，2008，93(7):940-949.

［5］Kim M C，Seong P H.An analytic model for situation assessment of nuclear power plant operators based on Bayesian inference［J］.Reliability Engineering and System Safety，2006，91(13):270-282.

［6］Cafiso S，Cava G L，Montella A.Safety index for evaluation of two-lane rural highways，2019［R］.Washington DC:Transportation Research Board of the National Academies，2007.

［7］Aguilera PA，Fernández A，Fernández R，et al.Bayesian networks in environmental modeling［EB/OL］.(2011-07-02)［2011-09-01］.http://www.sciencedirect.com/science/article/pii/S1364815211001472.

［8］Cooper G，Herskovits E.A Bayesian method for the induction of probabilistic network from data［J］.Machine Learning，1992，9(4):309-347.

［9］Maceachern SN.Estimating normal means with a conjugate style Dirichlet process prior［J］.Communications in Statistics:Simulation and Computation，1994，23(3):727-741.

［10］Friedman N，Koller D.Being Bayesian about network structure:a Bayesian approach to structure discovery in Bayesian networks［J］.Machine Learning，2003，50(1/2):95-125.

［11］Mitchell T.Machine learning［M］.New York:The McGraw-Hill Companies Inc，1997.

［12］Huang C，Darwiche A.Inference in belief networks:a procedural guide［J］.International Journal of Approximate Reasoning，1996，15(3):225-263.

［13］Madsen A，Jensen F.Lazy propagation:a junction tree inference algorithm based on lazy evaluation［J］.Artificial Intelligence，1999，113(1):203-245.

［14］Helman P，Veroff R，Atlas S R，et al.A Bayesian network classification methodology for gene expression data［J］.Journal of Computational Biology，2004，11(4):581-615.

［15］张杰，刘小明，贺玉龙，等.ARIMA模型在交通事故预测中的应用［J］.北京工业大学学报，2007，33(12):1295-1299.

Zhang Jie，Liu Xiaoming，He Yulong，et al.Application of ARIMA model in forecasting traffic accidents［J］.Journal of Beijing University of Technology，2007，33(12):1295-1299.(in Chinese)