半刚性基层沥青路面非连续结构强迫振动声效

李志栋 黄晓明 岳学军

(1东南大学交通学院，南京 210096)

(2河南高远路业集团，新乡 453000)

目前中国通车的7.41万km高速公路中，半刚性基层沥青路面占90%以上.裂缝是半刚性基层沥青路面比较典型的病害之一，但实际上因施工温度、土基固结、交通荷载及塑性变形累积等原因，半刚性基层底部出现的脱空、疏松等非连续病害及其次生病害越来越受到养护行业的重视［1-2］.

1996年，瑞典SKF公司首先发明了用振动脉冲仪来检测轴承的早期损伤［3］.1976年，日本新日铁株式会社研制了机器检测仪MCV-021，可分别在低频、中频和高频段检测轴承异常信号.目前国内有河南高远路业集团开发的连续式声效法连续性检测仪以及华南理工大学发明的定点式声振法水泥路面板底脱空检测仪［4］.

本文将在半刚性基层沥青路面的强迫振动分析基础上，建立其单自由度系统的强迫振动微分方程，并对其强迫振动声效特征进行研究.

1 路面单自由度振动体振动特性

1.1 路面振动特征及机理

半刚性基层沥青路面在低温、常温状态下接近弹性体，在冲击荷载作用下将发生振动，且产生振动噪声.通过对振动(噪声)参数的拾取、测量和处理，利用信号处理的频谱分析技术及其他信息，如温度、压力、变形、胀差、阻值、磁场等参数的变化，可初步判断路面结构健康状况，也可进一步判定结构非连续程度及其部位.

沥青路面在冲击力作用下将产生振动效应，满足

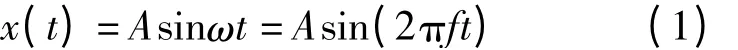
式中，x(t)为振动位移;A为位移幅值;ω为振动圆频率;f为振动频率.

采用连续和持续冲击装置对路面结构形成冲击加载，使路面结构弹性体产生强迫振动，从而在沥青混凝土这种弹性媒质(低温、常温时)中以该媒质特征速度传播压力、速度等综合扰动，形成既有压缩弹性又有剪切弹性的路面振动波，再经过路面结构辐射，形成空气中的振动噪声.

1.2 沥青路面层间连续性基本假设

路面结构是用各种混合料依路基、垫层、基层和面层不同结构组合铺筑而成的层状工程结构物［5］.

在行驶车轮的瞬时作用下，路面结构产生的黏-塑性变形很小，所以对于厚度较大、强度较高的高等级沥青路面，可将其视为线形弹性体，并应用弹性层状体系理论进行分析.连续性假设［6］:①各层连续、完全弹性、均质、各向同性;②层间接触面完全连续.

1.3 单自由度振动系统强迫振动微分方程假设

一般物体振动形式均可简化为弦、膜、棒和板的振动［7］，而半刚性基层沥青路面在非高温季节行车条件下多属于弹性体，且在板体四周及底部均受到约束，其振动也是由与板面垂直的外冲击荷载冲击产生，因此，沥青混凝土板体振动是一种单自由度弹性体强迫振动系统.沥青层厚度一般为0.04～0.22 m，宽度为4～7 m，其厚宽比约为1/130～1/30.100 kN荷载下设计弯沉为0.3 mm，其位移w远小于h/4，所以对其振动噪声分析时可以认为:①半刚性基层沥青路面板为弹性小挠度薄板，在厚度方向的应力为常数，中面的冲击振动位移仅为时间和平面坐标的函数;②中面内各点平行于中面的位移为零.

1.4 沥青路面板体强迫振动微分方程及其稳态解

1.4.1 单自由度系统振动微分方程［8］

板体振动微分方程的建立过程就是把实际振动系统理想化、离散化的力学模型转化为数学模型的过程，其等效振动微分方程通常表达为

式中，q为激励荷载;Me，Ce，Ke为系数;w为板体振动线位移.

1)振动微分方程及边界条件

根据假设，路面板体为四边简支板，中面各点横向位移为w(x，y，t)时，板上任意一点沿x，y，z三个方向位移分量u，v，w为

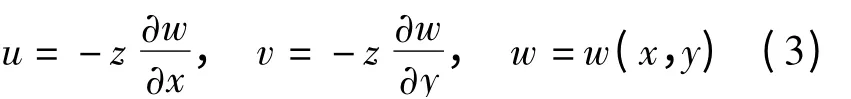
由Hamilton原理建立强迫振动微分方程，即

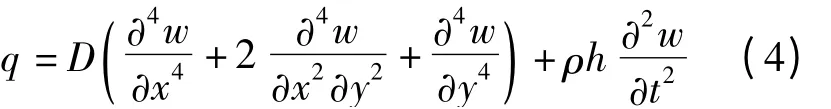
式中，q为激励荷载;h为板厚;ρ为板的密度;D为板的弯曲刚度.其边界条件为

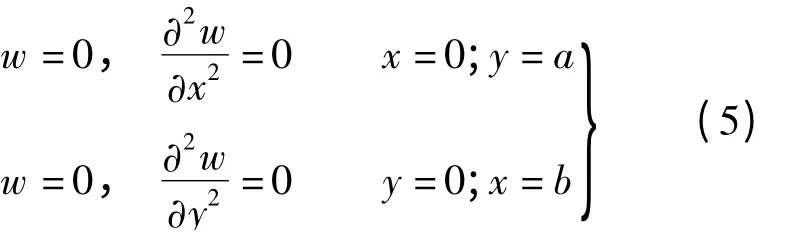
2)单自由度振动系统振型及固有频率

强迫振动微分方程的通解为

其特解假设为w=eiwt，由其求解的振型函数和固有频率函数为

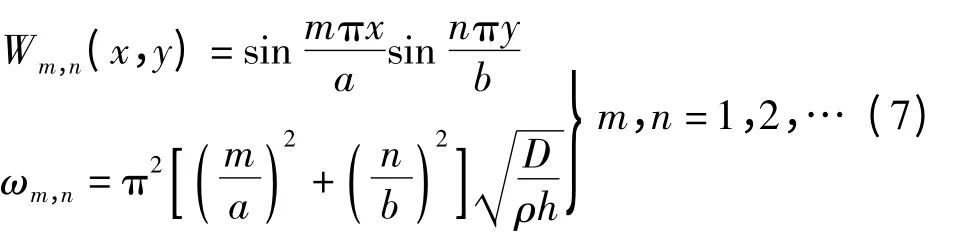
式中，Wm，n(x，y)为第m，n阶振型函数.

系统的固有频率对于一个系统是特有的、恒定的，但如果系统的质量M和弹性系数或刚度D发生变化，则其固有频率就将改变.

1.4.2 强迫振动微分方程

采用任意力冲击荷载和周期冲击力激励，迫使路面板体产生强迫振动，而路面板体系统对外荷载冲击所引起的状态响应可通过强迫振动方程来表征.

单自由度振动系统在频率为ω0的动荷载q(x，y，t)作用下的强迫振动方程及拉普拉斯变换方程为

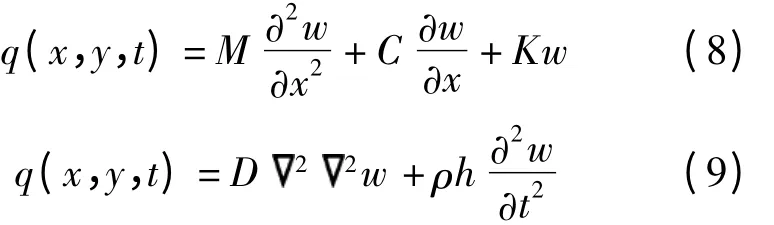
其求解如下:

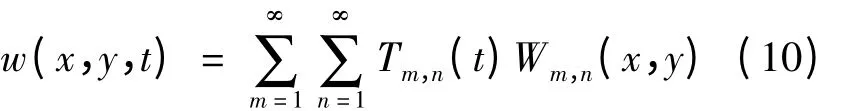
振型分量Tm，n(t)、第m，n阶广义力Pm，n(t)、广义质量Mm，n及零初值响应Tm，n(t)满足

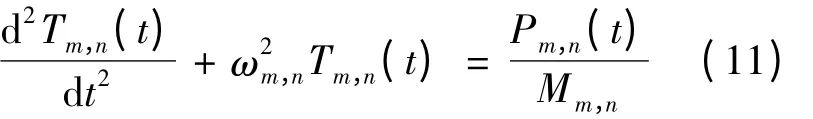
其中

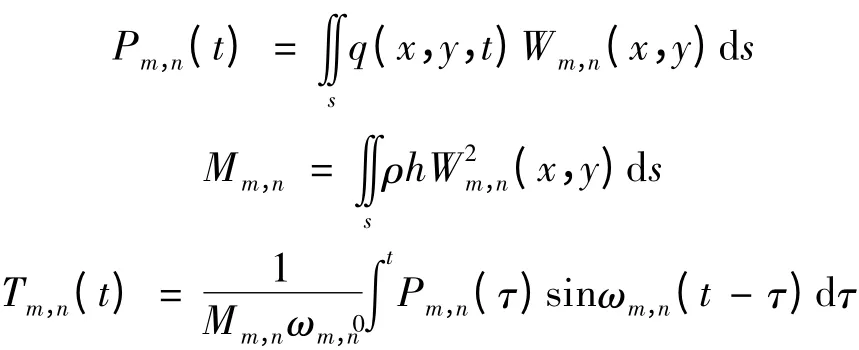
受集中正弦冲击周期力作用时需满足

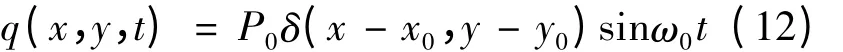
则

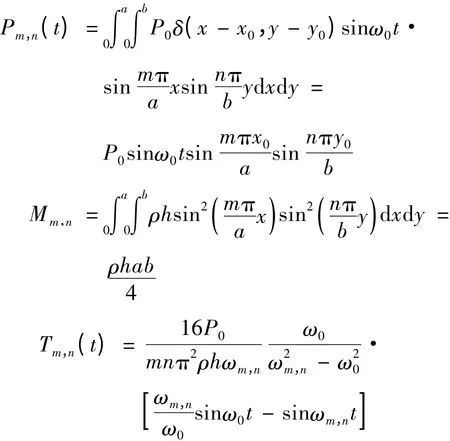
通过对式(9)～(12)的求解，可得到其瞬态解和稳态解两部分［9］，但瞬态解只在系统振动初期起作用，然后即消失，所以仅需求稳态解，即

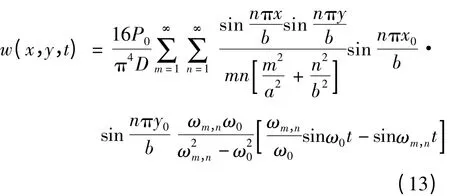
2 沥青路面冲击加载参数

2.1 强迫振动冲击参数

冲击加载模型采用如图1所示的齿轮状冲击荷载，每一个齿与路面接触相当于对路面一次冲击加载，梯形加载［10］时间t1=b/v=2.3 ms.加载轮行进速度3 m/s，齿距及轮缘与地接触宽度均为25 mm，接触长度为7 mm，荷载为150和1 000 N.

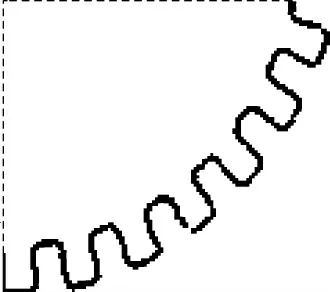
图1 激励轮模型(整个冲击轮的1/4)

采用移动冲击加载和固定点持续加载，分别模拟周期性加载力和恒定加载力的冲击作用.

2.2 路面结构物理参数

采用ABAQUS的声固耦合算法计算板体振动与声场的耦合问题，结构连续的路面计算模型尺寸为1 m×5 m.假定土基为弹性地基，面层、基层及底基层均为刚体，质量为M，第1阶频率为f，K为等效弹簧刚度(满足)，取K=41.426 kN/m，3阶模态频率分别为4.477 8，5.263 9，5.263 9 Hz.

路面结构组合及参数如图2所示(Hi为土层厚度，Ei为弹性模量，μ为泊松比)，路面纵向取10 m，沥青路面、基层、底基层及土基的密度分别为2.4×103，2.3×103，1.9×103，1.8×103kg/m3.

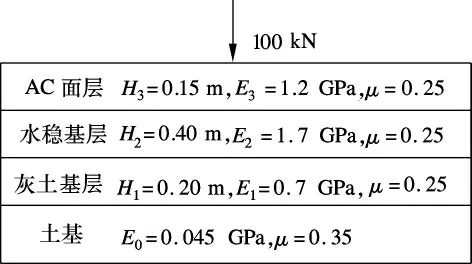
图2 路面结构层及参数

3 路面对荷载的响应

3.1 沥青路面强迫振动噪声机理

路面是一个由结构阻尼、黏性阻尼及摩擦阻尼共同作用的单自由度振动系统，在冲击荷载作用下，由于力、位置、速度、加速度等突然变化，路面系统将产生瞬态变化，即发生过渡性的冲击现象，属于非周期运动.而路面系统在强迫振动过程中产生的噪声是一种随机过程.

声压指介质中有声波传播与无声波传播时相比，介质内最大的压力变化，与声强的关系为

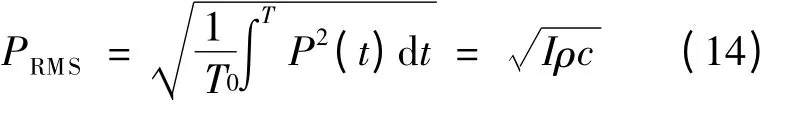
式中，I为声强;c为声音在介质中传播速度;T为积分时间;P(t)为介质内压力变化值.

3.2 声压对冲击力的敏感性

路面强迫振动应该选择合理的冲击力，本文选择150和1 000 N两种冲击荷载对正常的路面进行冲击振动，噪声响应频谱图如图3所示.

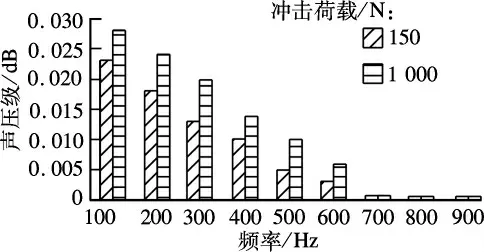
图3 2种荷载产生噪声响应频谱图

由图3可知，2种荷载产生的振动频率均集中在100～500 Hz的频带间，1 000 N冲击荷载较150 N的声压级高20%，为了增加识别性，采用1 000 N冲击荷载.

3.3 振动噪声声压对持续冲击力的敏感性

在t=0.002 5，0.554，1.003 s时对5个点进行观测，但因无法识别与各频率处声压规律不同的声场整体，加之人耳对高频敏感、低频不敏感，需要对检测噪声声压进行SPL处理，即

式中，PSPL为经处理后噪声的总声压级，dB;i为频率数;Pi为在第i个频率上的待测声压有效值，dB;Pref为参考声压，空气中取20μPa.

3.4 振动噪声声压对移动荷载冲击力的敏感性

同3.3节中取同样位置的5个点的PSPL分别为36.85，31.23，35.54，33.27，30.05 dB，比固定点冲击声压级平均降低6.5%，但仍集中在800 Hz频带.

4 不同连续性沥青路面强迫振动

4.1 半刚性基层沥青路面结构非连续病害机理

目前，高等级公路沥青路面以“强基薄面”为主要设计理念，基层基本上是水泥稳定碎(砾)石等半刚性材料，刚度大、强度高，随着水泥水化的发生，后期强度可以达到水泥混凝土强度，但因其干缩、温缩等缺点，容易导致反射裂缝的出现.特别在使用一段时间后由于动水冲刷、温度、湿度、荷载、材料、路基固结及不均匀沉降等因素存在，易产生结构层层间脱空或水稳层疏松等结构非连续现象，引发或加重路面裂缝、唧浆、坑槽、车辙、泛油、拥包等功能性病害和结构性病害［11-14］.这将改变设计时的完全连续成为理想状态，从层间连续到出现局部滑动的变化导致能够承受极限轴载降低40%［15］.

4.1.1 路基不均匀沉降及路基土的固结

当路基受不同地质、地貌条件影响时将产生不均匀沉降，当路基为深挖路堑或高填方路堤时，路基土失水固结时将产生一定收缩，在沉降与固结共同作用下，将引起半刚性基层沥青路面结构非连续的产生.

4.1.2 路基的压实度不足

由于施工受实际条件限制、赶工期、不满足最佳含水量、路基边缘碾压不到位等原因，路基压实度难以满足设计要求.

4.1.3 温度应力引起的半刚性基层拱起

在秋末冬初低温季节进行水稳基层施工时，材料均处于冷缩状态.成型后遇夏季高温时，基层受热将膨胀，当结构内产生并蓄积的温度应力超过临界值时，顶面约束较小的水稳基层将向上拱起，底部产生非连续.

4.1.4 土基的塑性变形累积

当车辆加载时，面层、基层、路基同时产生竖向变形，车辆通过后，由于半刚性基层刚性大，其产生变形完全回弹，而土基有部分残留变形，经过长期的作用，将在基层与土基间形成一个结构非连续区.

4.2 强迫振动噪声声压对结构连续状态的敏感性

半刚性基层沥青路面结构层分别为连续及非连续时，5个观测点的PSPL响应频谱如图4所示.

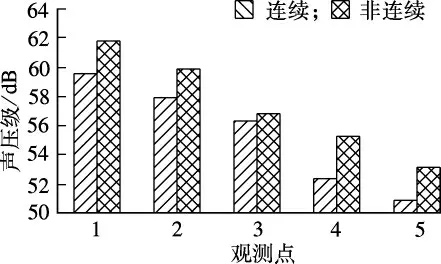
图4 观测点1～5连续与非连续区域噪声特征比较

由图4可知，沥青路面非连续时振动声压级超过连续时的10%～25%，尽管在800～1 000 Hz之间仍有分布，但主要能量集中在0～800Hz频带.其主要原因是沥青混凝土属多孔介质材料，其内部颗粒互相嵌挤形成不规则孔隙，由于颗粒的摩擦将对振动产生的声波能量传递起到一定的阻碍作用，使得振动声效能量产生一定的衰减，而当层间和结构内部出现非连续区，其黏性阻尼、摩擦阻尼以及结构阻尼均减小［16］，振动能量耗散减小，能够返回的声音能量将更多.

4.3 振动噪声声压对非连续区域面积的敏感性

假定在上述路面有限元计算模型中设置面积分别为1 m×4 m，2 m×4 m，3 m×4 m，4 m×4 m的4个非连续区，2个观测点处的声压对比如图5所示.

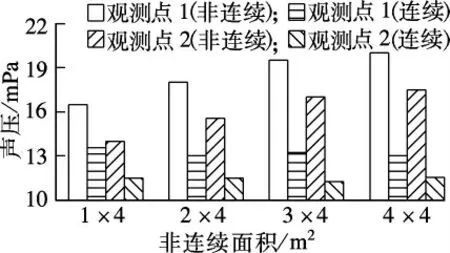
图5 观测点1，2处振动噪声声压对比

由图5可知，随着不连续面积的增加，2个观测点的振动噪声声压随之增加，但面积增加到3 m×4 m时，噪声声压增加幅度减小.

4.4 振动噪声声压对沥青路面板体尺寸的敏感性

由振型分量、板体振动方程稳态解以及频率函数的式(12)～(14)可知:①冲击振动噪声PSPL与板的尺寸有关，在其他参数相同的情况下，在一定尺寸范围内板越大，振动响应越大;②冲击振动噪声受板厚h影响，在其他参数相同的情况下，h越大，振动响应越小;③当冲击加载频率接近板体固有频率时，振动响应趋向最大，这是固有特性决定的.

总之，从理论上证明冲击振动声效与板体的尺寸(面积、厚度)有关，面积越大、厚度越小，其噪声特征越明显，反之越弱.

4.5 板体模量的影响

为了分析沥青路面在冬季寒冷或气温较低时劲度模量增加对其冲击振动噪声特征的影响，将面层弹性模量由原来的1.2 GPa提高到1.4 GPa，并分别采用如表1所示的加载方式加载.

由表1可知，当沥青路面面层弹性模量提高时，噪声声压级也将提高.同时，固定持续加载时产生的振动噪声特征较移动冲击加载时更为显著.

5 结论

1)在对半刚性基层沥青路面的冲击作用下，通过强迫振动噪声特征分析，可以定性地识别结构内部及层间的不连续程度.

2)半刚性基层沥青路面板体在低温、常温下属于单自由度振动系统，通过求解其强迫振动微分方程，证明沥青路面冲击振动噪声的PSPL对混凝土板体几何尺寸、模量、固有频率等最为敏感.

3)冲击荷载对沥青路面板体产生的振动噪声声压对非连续区域面积呈非线性增长关系，当非连续面积达到4 m×4 m时，振动声压的增加不显著.

4)半刚性基层沥青路面处于非连续状态时的强迫振动噪声能量很少超过800 Hz频带.

References)

［1］沈金安，李福普，陈景.高速公路沥青路面早期损坏分析与防治对策［M］.北京:人民交通出版社，2004.

［2］巴桑顿珠，黄晓明.西藏沥青路面裂缝温度疲劳扩展寿命分析［J］.东南大学学报:自然科学版，2006，36(6):1013-1017.

Basang Dunzhu，Huang Xiaoming.Analysis for fatigue life of asphalt pavement temperature crack in Tibet［J］.Journal of Southeast University:Natural Science Edition，2006，36(6):1013-1017.(in Chinese)

［3］刘瑞扬，王毓民.铁路货车滚动轴承早期故障轨边声学诊断系统(TADS)原理及应用［M］.北京:中国铁道出版社，2005.

［4］彭永恒，陈静云，潘宝峰，等.声振法对刚性路面板脱空状况检测应用的研究［J］.公路交通科技，2005，22(3):54-57.

Peng Yongheng，Chen Jingyun，Pan Baofeng，et al.Application study of acoustic-vibration in detection of rigid pavement slab cavern［J］.Journal of Highway and Transportation Research and Development，2005，22(3):54-57.(in Chinese)

［5］郭乃胜，石峰，赵颖华，等.沥青路面层间粘结性能的

黏弹性有限元分析［J］.大连海事大学学报，2009，35(4):81-85.

Guo Naisheng，Shi Feng，Zhao Yinghua，et al.Viscoelasticity finite element analysis of interface bonding behaviors of asphalt pavement［J］.Journal of Dalian Maritime University，2009，35(4):81-85.(in Chinese)

［6］邓学钧，张登良，许志鸿.路基路面工程［M］.3版.北京:人民交通出版社，2008.

［7］杜功焕，朱哲民，龚秀芬.声学基础(上册)［M］.南京:南京大学出版社，1981.

［8］Meada D J，Markus S.The forced vibration of a threelayer，damped sandwich beam with arbitrary boundary conditions［J］.Journal of Sound and Vibration，1968，10(2):163-175.

［9］黄传志.多维太沙基固结微分方程求解［J］.岩土工程学报，1991，13(1):34-45.

Huang Chuanzhi.A solution to Terzaghi's multidimensional consolidation differential equation［J］.Chinese Journal of Geotechnical Engineering，1991，13(1):34-45.(in Chinese)

［10］卢正，姚海林，骆行文.矩形移动荷载作用下路面-双层地基系统三维振动分析［J］.岩土力学，2009，30(11):3493-3499.

Lu Zheng，Yao Hailin，Luo Xingwen.3D vibration of pavement and double-layered subgrade coupled system subjected to a rectangular moving load［J］.Rock and Soil Mechanics，2009，30(11):3493-3499.(in Chinese)

［11］Strategic Highway Research Program National Research Council.Materials and procedures for sealing and filling cracks in asphalt-surfaced pavements manual of practice，FHWA-RD-99-147［R］.Washington DC:Strategic Highway Research Program National Research Council，1999.

［12］Scholz T V，Terrel R L，AI-Joaib A，et al.Water sensitivity:binder validation，SHRP-A-402［R］.Washington DC:Strategic Highway Research Program National Research Council，1994.

［13］Sousa JB，Craus J，Monismith C L.Summary report on permanent deformation in asphalt concrete，SHRPA/IR-91-104［R］.Washington DC:Institute of Transportation Studies， University of California Berkeley，1991.

［14］Strategic Highway Research Program National Research Council.Distress identification manual for the longterm pavement performance project，SHRP-P-338［R］.Washington DC:Strategic Highway Research Program National Research Council，1993.

［15］曾梦澜，马正军，龚平，等.面-基层间接触条件对半刚性沥青混凝土路面极限轴载的影响［J］.公路，2005(1):79-83.

Zeng Menglan，Ma Zhengjun，Gong Ping，et al.Effects of base-surface inter-layer contact conditions of semi-rigid asphalt pavement on ultimate axle load［J］.Highway，2005(1):79-83.(in Chinese)

［16］陈端石，赵玫，周海亭.动力机械振动与噪声学［M］.上海:上海交通大学出版社，1996.