爆炸冲击对多层钢框架连续倒塌性能的影响

宋 拓 吕令毅

(东南大学土木工程学院，南京 210096)

连续倒塌是指建筑物在正常使用状态下由于突发事件导致结构局部构件破坏，并且这种破坏沿着其他构件不断地传递和扩散，最终导致建筑物发生与初始破坏不相称的大面积倒塌.对于连续倒塌的分析方法，文献［1-2］提出的备用荷载路径法(AP法)由于其高效的分析效率和良好的实用性被广泛地采用，文献［3-4］对此已有了较为深入的研究.然而，备用荷载路径法的最大的缺点就是不考虑构件移除的初始条件及其带来的附加荷载，对附加荷载在结构内部产生的影响不予考虑，因此对于由碰撞、爆炸引起的连续倒塌问题，备用荷载路径法分析并不能令人信服.近年来，爆炸对建筑物冲击作用的相关研究不断展开，文献［5］模拟和研究了钢柱和平面钢框架在爆炸荷载作用下的动力响应和破坏形态，文献［6］假定爆炸发生在建筑物外部，研究了外爆炸冲击对框架结构倒塌性能的影响.本文以三维5层钢框架结构为例，采用有限元软件SAP2000对钢框架在爆炸冲击下的连续倒塌性能行了研究.

1 结构原型与有限元模型

结构原型平面尺寸为20 m×15 m，柱网布置如图1所示，框架竖向5层，每层层高4 m.柱:H400 mm×300 mm×12 mm×14 mm;主梁:H300 mm×250 mm×10 mm×12 mm;无次梁与支撑.框架结构钢选用Q235B，梁与柱连接处均采用刚接，底层柱与基础固结，每一层布置厚度为100 mm的C30级混凝土楼板.除梁、板、柱的自重荷载SG外，结构施加荷载如下:1～4层施加设备荷载SE(8 kN/m2)，楼面活荷载SL(2 kN/m2)，屋顶层不考虑设备荷载，只施加楼面活荷载，如图2所示.1～4层最外一圈的框架主梁上施加墙体线荷载SW(8 kN/m)，分析过程中不考虑风荷载作用.

图1 结构柱网平面图(单位:m)

图2 横向框架立面图(单位:m)

采用有限元软件SAP2000对原型结构进行建模，Q235B钢的屈服应力σy=235 MPa，极限应力σu=390 MPa，应力-应变关系如图3所示，混凝土材料模型选用软件内置的C30混凝土模型.

图3 钢的应力-应变曲线

连续倒塌分析需考虑构件屈服后的受力和变形性能，因此为梁、柱指定了基于FEMA356［7］定义的塑性铰，每个塑性铰的力-位移曲线都由A～E五个点来进行控制，同时在塑性铰的屈服点B和承载极限点C之间定义了PIO(可立即使用)、PLS(保障生命安全)、PCP(防止倒塌)3个点代表塑性铰的不同能力水平(见图4).当塑性铰的转角超越了PCP点，即可认为塑性铰处已发生破坏，该构件无法继续承载.对于PIO，PLS，PCP三个点，塑性铰转角限值分别为θy，6θy，8θy;θy为截面屈服转角［7］.

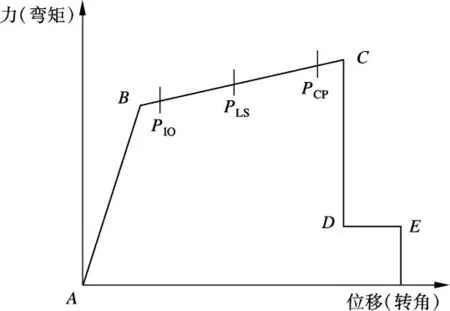
图4 塑性铰的力-位移曲线

2 连续倒塌分析

基于AP法，利用SAP2000进行连续倒塌分析，在分析过程中考虑P-Δ效应.根据是否考虑结构的动力效应，连续倒塌分析可分为静力非线性分析和动力非线性分析.在动力非线性分析中考虑爆炸冲击荷载的影响，将其作为第3种分析工况.参照文献［1-2］的做法，同时考虑结构布置及荷载分布情况，选择底层的A1柱(角柱)、B1柱(短边中柱)、A3柱(长边中柱)、B3柱(内柱)作为失效柱(见图1)，分别进行连续倒塌分析.

2.1 静力非线性分析

2.1.1 荷载工况

静力非线性分析工况中，结构基本荷载取S=1.25(SG+SE+SW)+0.5 SL［2］，考虑目标柱移除瞬间上部荷载的动力放大效应，应将基本荷载乘以动力放大系数(DIF)作为分析荷载.对于采用不同构件的钢框架结构，最新的UFC—2009［2］推荐的DIF值在区间［1.2，2.0］内，偏于安全考虑，DIF取最大值2.0.

2.1.2 分析结果

静力非线性工况的分析结果如表1所示.

表1 静力非线性分析结果

分析结果表明，在分别抽取了角柱、边柱和内柱的情况下，钢框架依然具有良好的承载力和抗变形性能.其中抽取角柱A1的情况最为不利，这与文献［1］的分析结果是一致的，柱顶节点的竖向位移达到了－64.7 mm，同时框架的内柱出现了4个塑性铰(B点).由于静力非线性分析的动力放大系数偏大，且在最不利的情况下塑性铰也处于很低的变形水平，因此该框架不会发生连续倒塌.

2.2 动力非线性分析

2.2.1 荷载工况

基于AP法的动力连续倒塌分析时，目标柱顶的荷载加载时程如图5所示.首先在结构上作用基本荷载S=1.25(SG+SE+SW)+0.5 SL，然后计算目标柱在初始荷载下的静内力P0(弯矩、剪力、轴力).在进行动力分析前，移除目标柱，将P0反向加载到目标柱承载处以模拟目标柱未移除的状态，并维持t0时间以保证该状态的稳定.假定在t0时间后移除目标柱，则柱的内力P0将在tp时间内逐步衰减直到为零，这样就能模拟目标柱在移除时，结构的内力及位移的时程变化［2-3］.

图5 柱顶荷载加载曲线

分析前还需对目标柱移除后的剩余结构进行模态分析，提取对应失效位移方向的模态周期Tp，用来计算目标柱内力的卸载时间tp.本文取t0=1 s，tp=0.1 Tp［1-3］，结构阻尼采用瑞利阻尼，模态阻尼比取0.02.

2.2.2 分析结果

动力非线性工况的分析结果如表2所示.

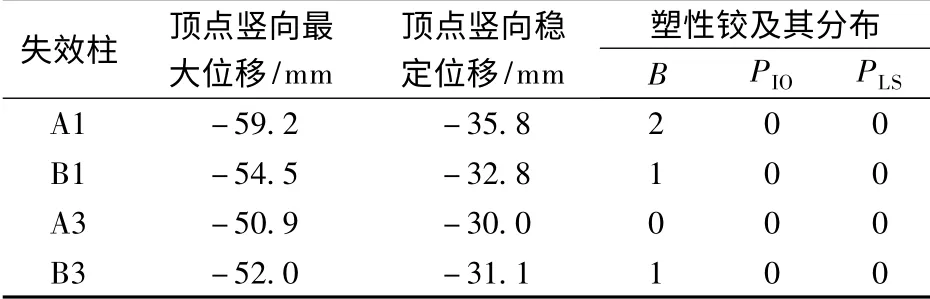
表2 动力非线性分析结果

在动力分析工况下，抽取角柱A1依然为最不利情况，在柱失效后结构振荡的过程中，柱顶节点最大位移为－59.2 mm，振荡的稳定位移为－35.8 mm，由仅出现2个塑性铰(B点)的情况可以判断，结构在抽取角柱的情况下依然具有良好的承载能力并处于很低的变形水平，因此，钢框架不会发生连续倒塌.

2.3 爆炸冲击下的动力非线性分析

2.3.1 荷载工况

爆炸是导致建筑结构局部破坏、整体倒塌的重要原因之一，在距离爆炸点极近的情况下，少量的炸药也能够造成数千千帕的冲击荷载.如果爆炸针对钢结构柱，目标柱将严重屈服甚至破坏从而丧失承载能力，同时周围的构件也要受到爆炸冲击荷载的作用.此外，爆炸产生的冲击荷载将随距离起爆点的径向距离增加而急剧衰减，因此爆炸的影响范围是有限的.

根据爆炸动力学，无限理想大气中TNT炸药的冲击波阵面超压(ΔP，kN/m2)与爆炸距离和炸药量的关系为［8］

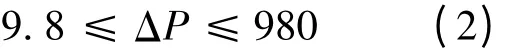
爆炸超压荷载时程采用对气体扩散有限制情况下的爆炸典型超压时程曲线［5，9］(见图6).

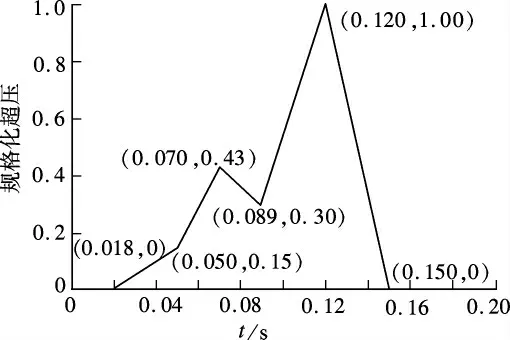
图6 爆炸典型超压曲线

假定起爆点设定在目标柱的中点处，可以分别计算相邻梁、板、柱所受到的爆炸超压峰值，同时设定结构在分析开始的第1 s前无外荷载施加;1 s后，爆炸超压作用在结构上，可得到实际采用的爆炸冲击荷载时程曲线(见图7);爆炸荷载的加载方式如图8所示.由于爆炸冲击波传播10 m左右的平均时间仅需十几毫秒［10］，因此忽略爆炸冲击波到达不同构件的时间差，认为荷载同时作用到构件上.采用式(1)和(2)分别计算不同距离下的爆炸超压峰值(见表3).

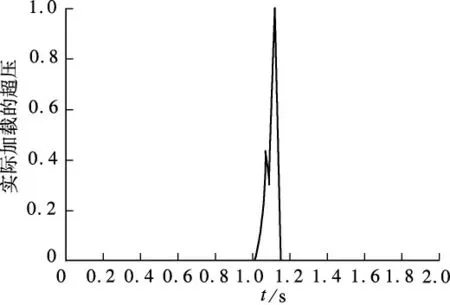
图7 爆炸冲击荷载时程曲线

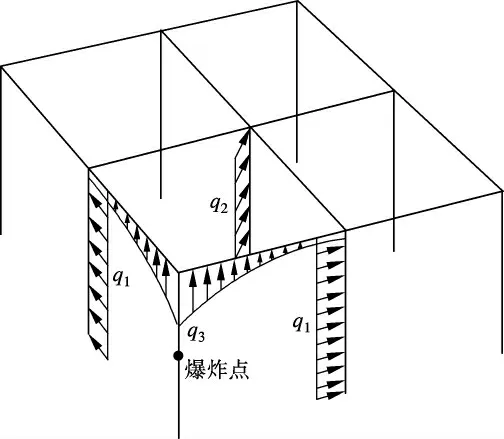
图8 爆炸荷载加载示意图

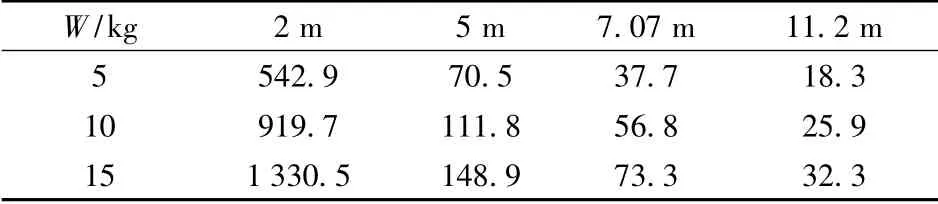
表3 不同距离的爆炸超压峰值 kN/m2

2.3.2 分析结果

汇总各工况下的分析结果，如图9、图10及表4、表5所示.

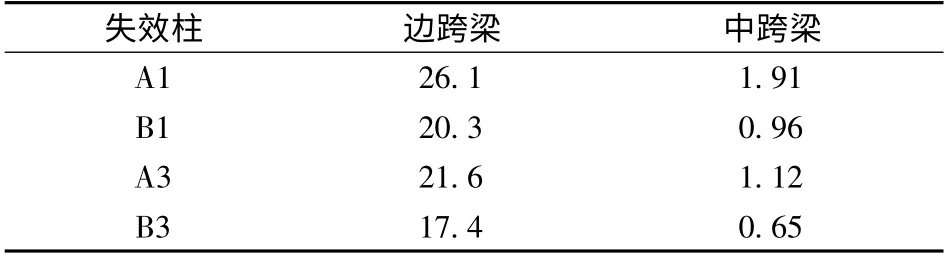
表4 15 kg炸药爆炸点四周梁的平均最大扭矩 kN·m

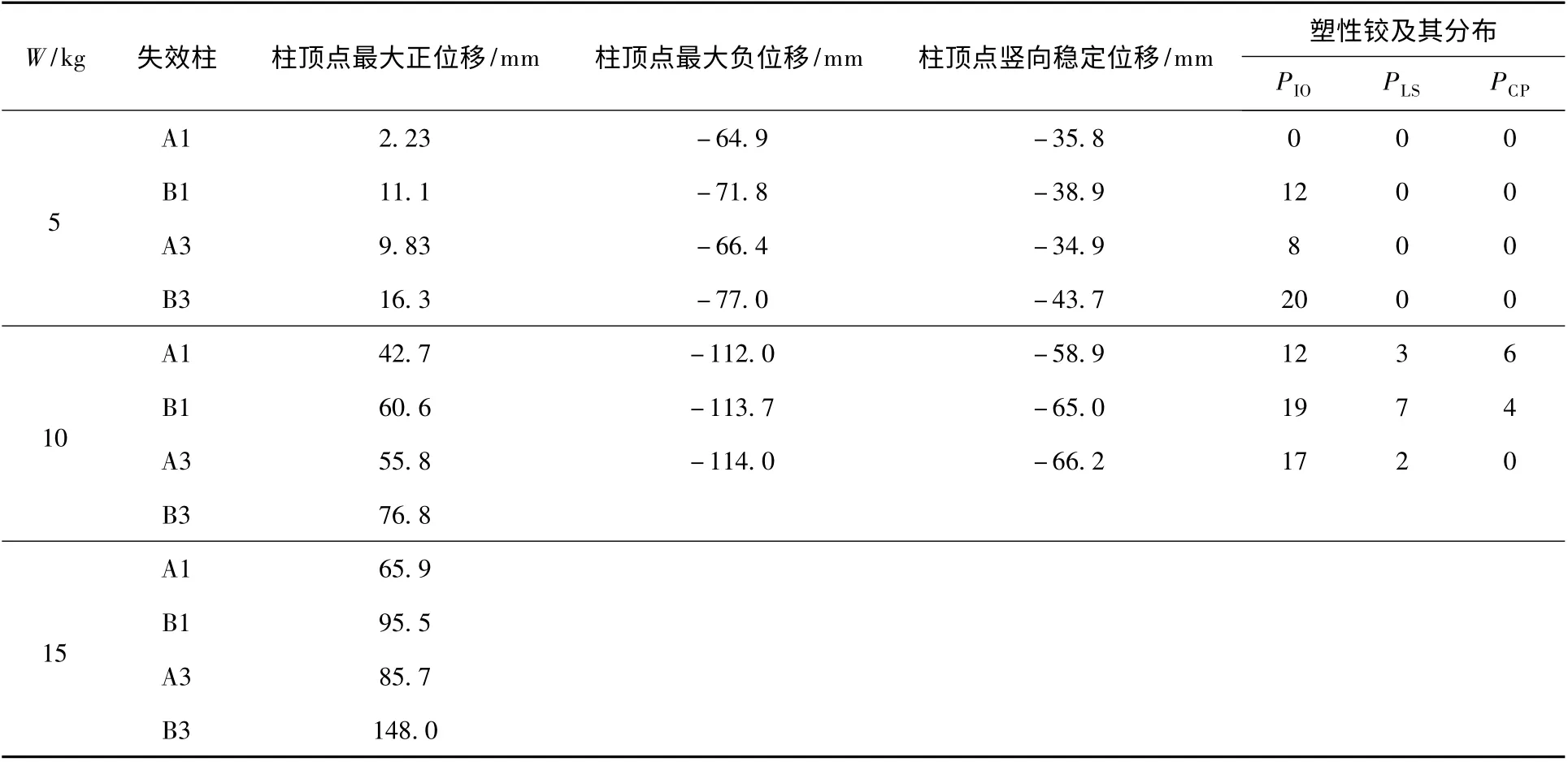
表5 爆炸荷载作用下的连续倒塌分析结果

图9 柱爆炸失效顶点位移时程曲线

图10 15 kg爆炸导致A3柱失效时A轴框架塑性铰图

由分析可见，考虑了爆炸荷载后，钢框架连续倒塌分析的结果发生了极大的变化.在5 kg TNT炸药的爆炸荷载作用下，目标柱破坏，柱顶节点在猛烈的冲击波作用下会有向上的瞬时位移，并且爆炸点周围的梁和柱构件出现了数个LS级塑性铰，但没有CP级塑性铰.由于塑性铰的变形水平较低，爆炸结束后依然能得到稳定的位移，不会发生局部垮塌，但与动力非线性结果相比，柱顶节点最大负位移和稳定负位移增大了不少，其中抽取内柱的工况下2种位移都增大了40%以上，说明爆炸冲击瞬间产生的塑性铰将结构的承载力削弱不少.在10 kg炸药爆炸的作用下，起爆点四周的梁上出现了数个CP级塑性铰，说明构件进入严重的塑性状态，可以判定为局部破坏.在边柱和角柱破坏的情况下，计算依然可以得到稳定的位移，说明结构没有发生整体垮塌;但在内柱破坏时，由于冲击荷载过大导致周围梁柱大面积屈服，计算难以继续，结构则发生整体倒塌.在15 kg炸药爆炸的作用下，无论选取哪一根目标柱，巨大的冲击荷载都会使结构在0.3 s内构件迅速破坏、结构整体倒塌.

由分析过程中还可发现，与动力非线性分析相比，爆炸冲击作用下的动力非线性分析中，结构的最不利柱由角柱变为了内柱.经过对比计算结果和爆炸荷载分析发现，爆炸冲击波在起爆点四周梁柱上产生的线荷载并不是引起结构倒塌的主要原因，而起爆点四周上部的楼板由于迎爆面很大导致板上冲击面荷载巨大，楼板向上迅速挠曲，周围的梁承受了很大的弯、剪荷载.实际上，钢筋和混凝土材料在爆炸荷载的作用下，会经历高达10～1 000 s－1的应变率，在这种高应变率情况下，钢筋的强度能够提高50%，混凝土的抗压强度能够提高100%［11-12］，板的破坏耗能机制将得不到充分发挥.此外，相对于中跨梁，爆炸点周围的边跨梁会因单侧楼板的受冲击作用而产生较大扭矩(见表4)，扭矩会降低梁承受的临界弯矩，使钢梁更容易整体失稳.因此楼板在爆炸导致钢结构倒塌的过程中起了非常不利的作用.

3 结论

1)由于不考虑构件初始破坏因素引起的附加荷载，传统的备用荷载路径法在框架连续倒塌分析中具有一定的局限性.

2)爆炸荷载作用下的连续倒塌分析不应采用简单的备用荷载路径法进行分析，应考虑爆炸冲击时程下的备用荷载路径法分析或者是利用直接模拟法进行连续倒塌分析.

3)楼板由于受冲击面很大导致其成为爆炸荷载下影响框架结构安全性的不利因素，因此在保证楼板承载能力的同时，有必要对如何提高楼板在冲击荷载下的抗爆耗能性进行更加深入的研究.

References)

［1］US General Services Administration.Progressive collapse analysis and design guidelines for new federal office buildings and major modernization projects［S］.Washington DC:GSA，2003.

［2］Department of Defense.Unified facilities criteria，design of buildings to resist progressive collapse［S］.Washington DC:DoD，2009.

［3］ 谢甫哲，舒赣平，凤俊敏.基于抽柱法的钢框架连续倒塌分析［J］.东南大学学报:自然科学版，2010，40(1):154-159.

Xie Fuzhe，Shu Ganping，Feng Junmin.Progressive collapse analysis of steel frame structure using removing column method［J］.Journal of Southeast University:Natural Science Edition，2010，40(1):154-159.(in Chinese)

［4］马人乐，林国铎，陈俊岭，等.水平分布柱间支撑对多高层钢框架抗连续倒塌性能的影响［J］.东南大学学报:自然科学版，2009，39(6):1200-1205.

Ma Renle，Lin Guoduo，Chen Junling，et al.Effects of horizontal column-and-braces on progressive collapse resistance of multi-story and high-rise steel frame［J］.Journal of Southeast University:Natural Science Edition，2009，39(6):1200-1205.(in Chinese)

［5］李忠献，刘志侠，丁阳.爆炸荷载作用下钢结构的动力响应与破坏模式［J］.建筑结构学报，2008，29(4):106-111.

Li Zhongxian，Liu Zhixia，Ding Yang.Dynamic responses and failure modes of steel structures under blast loading［J］.Journal of Building Structures，2008，29(4):106-111.(in Chinese)

［6］阎石，王积慧，王丹，等.爆炸荷载作用下框架结构的连续倒塌机理分析［J］.工程力学，2009(S1):242-247.

Yan Shi，Wang Jihui，Wang Dan，et al.Mechanism analysis on progressive collapse of RC frame structure under blast effect［J］.Engineering Mechanics，2009(S1):242-247.(in Chinese)

［7］Federal Emergency Management Agency.Prestandard and commentary for the seismic rehabilitation of buildings［S］.Washington DC:FEMA，2000.

［8］亨利奇J.爆炸动力学及其应用［M］.北京:科学出版社，1987:126-127.

［9］Smith P D，Hetherington J G.Blast and ballistic loading of structures［M］.Oxford:Butterworth-Heinemann，1994.

［10］涉谷尧，矶部俊郎.关于爆炸冲击波速度衰减实验的研究［J］.矿业安全与环保，1985(1):63-69.

Shibuya Yao，Isobe Toshiro.Research on the experiment of velocity attenuation of blast shock wave［J］.Mining Safety＆Environmental Protection，1985(1):63-69.(in Chinese)

［11］Malvar L J，Ross C A.Review of strain rate effects for concrete in tension［J］.ACI Materials Journal，1999，96(5):614-616.

［12］Bischoff P H，Perry S H.Compressive behavior of concrete at high strain rate［J］.Materials and Structures，1991，24(144):425-450.