基于可交易价值的资本资产定价模型实证研究

张 普

（常州大学 经济管理学院，江苏 常州 213164）

一、引 言

资本资产定价问题是现代金融学的核心问题之一，且相关的研究大多可归结为对资本资产价格影响因素的探索。以股票为例，现有研究多集中于对规模因素、上市公司的投资收益率（E/P值）、财务杠杆、净资产市值比、动能及反转、流动性以及投资者心理等方面，并已经取得了相当多的研究成果。

然而，这些研究的思路一般来源于对股价的长期观察，而如果能从股票价格的形成过程中探索其可能的影响因素，则无疑是一种全新的的尝试。文献［1］曾从资产链的角度剖析了经济生活中资产价值的不断转移、变化和创造过程，即“实物资产→公司资产→资本资产→衍生资产”的过程，认为其中包涵了由各种金融创新带来的资产形态及价值的演变。这里，股票的上市过程即为资产链中由公司资产到资本资产变化过程的具体表现。较公司资产而言，资本资产最重要的特征在于其“可交易性”。可交易，使公司资产实现了股份化、为资本资产带来了流动性和波动性，并且，这些特征伴随着资本资产交易的始终，随时影响着资本资产的收益，是资本资产未来价格变化的基本条件和源泉。

因此，从股票价格的形成过程看，可交易必然具有价值。将可交易价值引入资本资产定价模型，并利用一些市场中容易观察到的因素来描述可交易价值，进而对股票的价格和收益做出合理的解释，是本文的主要研究目标，同时也是本文的主要创新之处。

二、可交易价值的构成分析及模型的建立

（一）可交易价值的构成分析

根据资产链的思想，结合对公司资产上市交易过程的分析，可以将股票的可交易过程分解为三个金融创新环节：首先，公司上市前必须进行股份化，将净资产进行拆分，使其成为价格较低、便于投资者买卖的形式；其次，资产上市交易，股份可流通，具有了流动性；最后，可流通使得股票价格的波动成为可能，资产具有了波动性［2］。在这个过程中，资产的形态或价值发生了连续的变化，并最终形成了我们在市场上见到的股票价格和收益。

1.股份化过程与股票价格因子

可交易过程中，股份化是基础和必备条件，只有当公司资产具备了单位价值低、便于投资者买卖的形态之后，公司股份的“可交易”才成为可能。经济学中的供求关系理论能对此作出合理的解释，即市场面对股份化前后的单位资产价格，会具有完全不同的需求函数，以此类推，在面对高价股和低价股时，投资者和市场也会有不同的需求和态度，进而也就会影响到相关股票的价格和收益。这一点，从有关股份分割的文献中可以得到间接的论证［3-5］。因此我们认为，股价因子是影响股票价格和收益的因素之一。

2.可流通过程与流动性因子

作为可交易过程中最核心的环节，“流动性”已经受到了相当的关注。著名的“流动性期权理论”就从流动性价值的角度计算了证券“可交易（Marketability）”的价值［6-7］，认为流动性缺失是导致不可交易或交易受限股票产生折价的主要原因。此外，资产定价领域中关于流动性价值的研究颇多，但通常并不涉及“可交易价值”的概念，而是讨论流动性水平或流动性风险对资产价格和收益的影响［8-10］。因此，无论是从理论研究的角度，还是根据实践中的经验，流动性因子都应是可交易价值分析中必须考虑的因素。

3.可波动过程与波动性因子

可波动过程是一个通常不为人们所认识的过程。但通过对股票价格行为的观察，不难发现真正给投资者带来收益的，绝不仅仅是“能卖”，而是“能以不同的价格卖”。文献［7］曾指出“收益波动率是决定折价程度的主要因素”，其实证结论也表明不可交易股票现实的折价程度往往接近甚至高于理论模型得出的最大值，这就使我们必须考虑可交易价值中波动性价值的存在。近年来，已经有研究发现波动因子对证券价格具有解释能力［2,11-12］。因此，波动性因子也应是我们研究可交易价值构成时应考虑的影响因素。

（二）模型的建立

在考虑股票可交易价值的基础上，以CAPM模型为基础建立模型，可得下式：

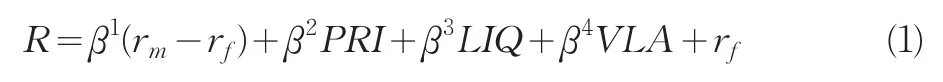
其中，R为个股或组合的收益率；rf为无风险收益率；rm为市场收益率；PRI、LIQ和VLA分别为价格因子、流动性因子和波动性因子；β1、β2、β3和β4则分别为系统风险因子、价格因子、流动性因子和波动性因子对股票风险收益率的影响系数。

三、实证分析

（一）样本选择

由于我国股市在2006-2008年曾出现一轮非理性的急涨-急跌行情，因此本文选择2003年5月12日至2005年3月11日间在我国沪深股市主板上市交易的所有A股的日交易数据进行实证，并依下列原则筛选样本：剔除在样本期间内被特别处理或被其他处理的个股；剔除净资产小于零的个股；剔除新上市个股前20个交易日的交易数据。经过筛选，有效样本共涉及448个交易日，1182支个股。

令 Ri,j、Prii,j、ExRi,j、Vlai,j以及 rm,i,j（i=1,2…1182；j=1,2…448）分别为个股i在其第j个交易日的对数收益率、收盘价、换手率、波动率以及流通市值加权平均市场日收益率，分别作为个股收益率、价格因子、流动性因子、波动性因子以及市场收益率的代理指标，其中波动率根据Garch（1，1）模型计算而得，并记rf,j为第j个交易日的日无风险收益率。所有数据来源于锐思（RESSET）数据库。样本期间如遇个股停盘，则停盘日相关数据记为空值，不参加后续计算。

（二）数据分组及描述

首先，在每个交易日j，将所有有交易的个股按股价Prii,j-1从低到高排序，并以约3:4:3的比例分成三组，分别记为LP、MP、HP组，第一组为股价最低的30%，第二组为股价居中的40%，第三组则为股价最高的30%；

其次，在每个交易日j，将所有有交易的个股按换手率ExRi,j-1从低到高排序，并以约3:4:3的比例分成三组，分别记为LE、ME、HE组；

再次，同样在每个交易日j，将所有有交易的个股按波动率Vlai,j-1从低到高排序，并以约3:4:3的比例分成三组，分别记为LV、MV、HV组；

最后，将上述三种分组结果交叉，可得27个组合，并用三位字母以股价、换手率和波动率的顺序进行标记。例如，第LMH组代表股价低，换手率中，波动率高的个股组合；第MHL组则代表股价中，换手率高，波动率低的个股组合；以此类推。

分组完成后，对每一个交易日j，求每个组合k的算术平均对数收益率、算术平均收盘价、算术平均换手率、算术平均Garch波动率和算术平均市场收益率，分别记为P_Rk,j、P_Prik,j、 P_ExRk,j、 P_Vlak,j和 P_rm,k,j（k=1,2…27； j=1,2…448）。

27个组合日收益率数据的描述统计分析如表1所示。

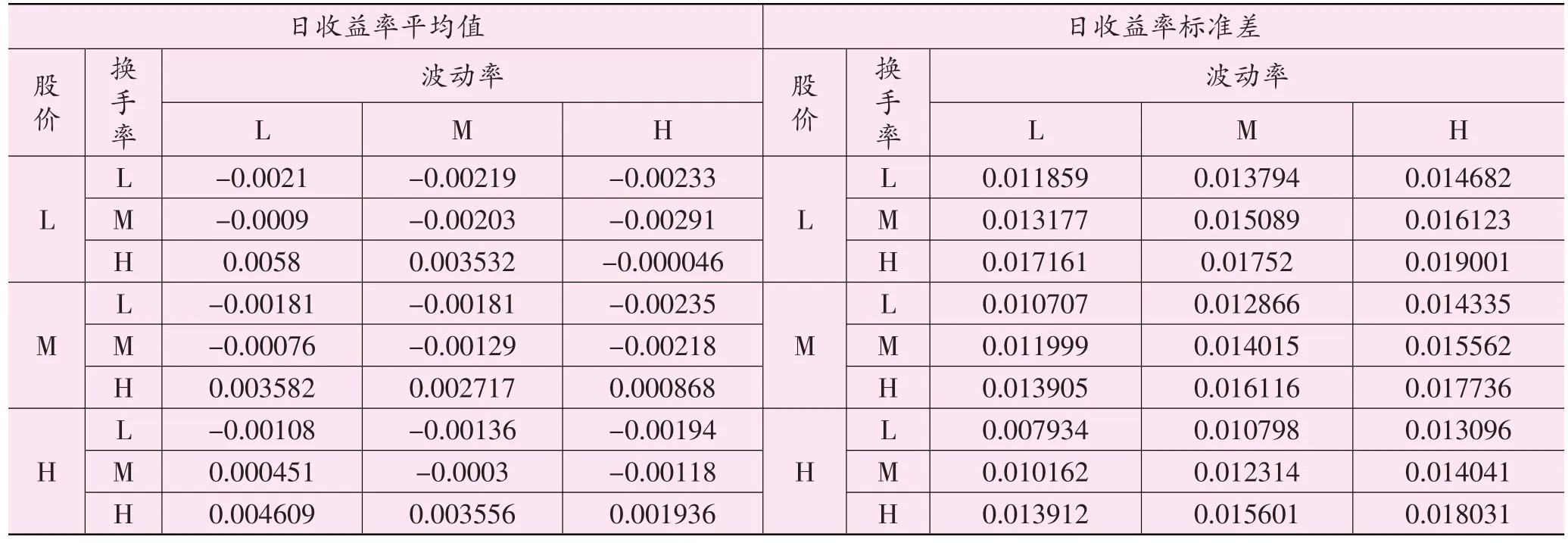
表1 27个股票组合日交易数据描述统计分析

总体上说，27个组合的日收益率特征呈明显的规律变化：随着股价的升高，收益率的均值增加而标准差减小，说明高价股组合收益更高且更稳定；随着换手率的提高，收益率均值增加但标准差也在增加，说明流动性好的组合虽然可以获取高收益但也会面临高风险；随着波动率的上升，收益率的均值降低同时标准差增大，说明波动性大的组合不仅收益低而且风险大。结合本文样本区间内我国股市的交易状况，上述结果是与实际情况基本相符的。

（三）实证过程及结果分析

对样本数据采用横截面回归法进行实证，该方法包括两轮回归：第一轮为时间序列回归，对组合的时间序列数据进行回归，以得到各组合回归系数的估计值；第二轮为横截面回归，即对时间序列回归中得到的各组合的回归系数进行横截面回归，以验证模型的科学性。

1.时间序列回归

将（1）式改写为：

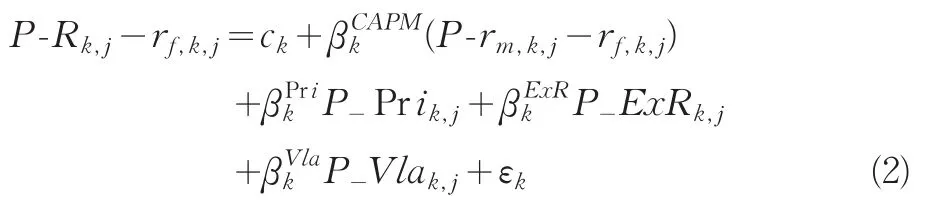
根据（2）式对27个组合中前443个数据点的样本数据进行时间序列回归，可得回归系数和相关回归结果如表2所示。

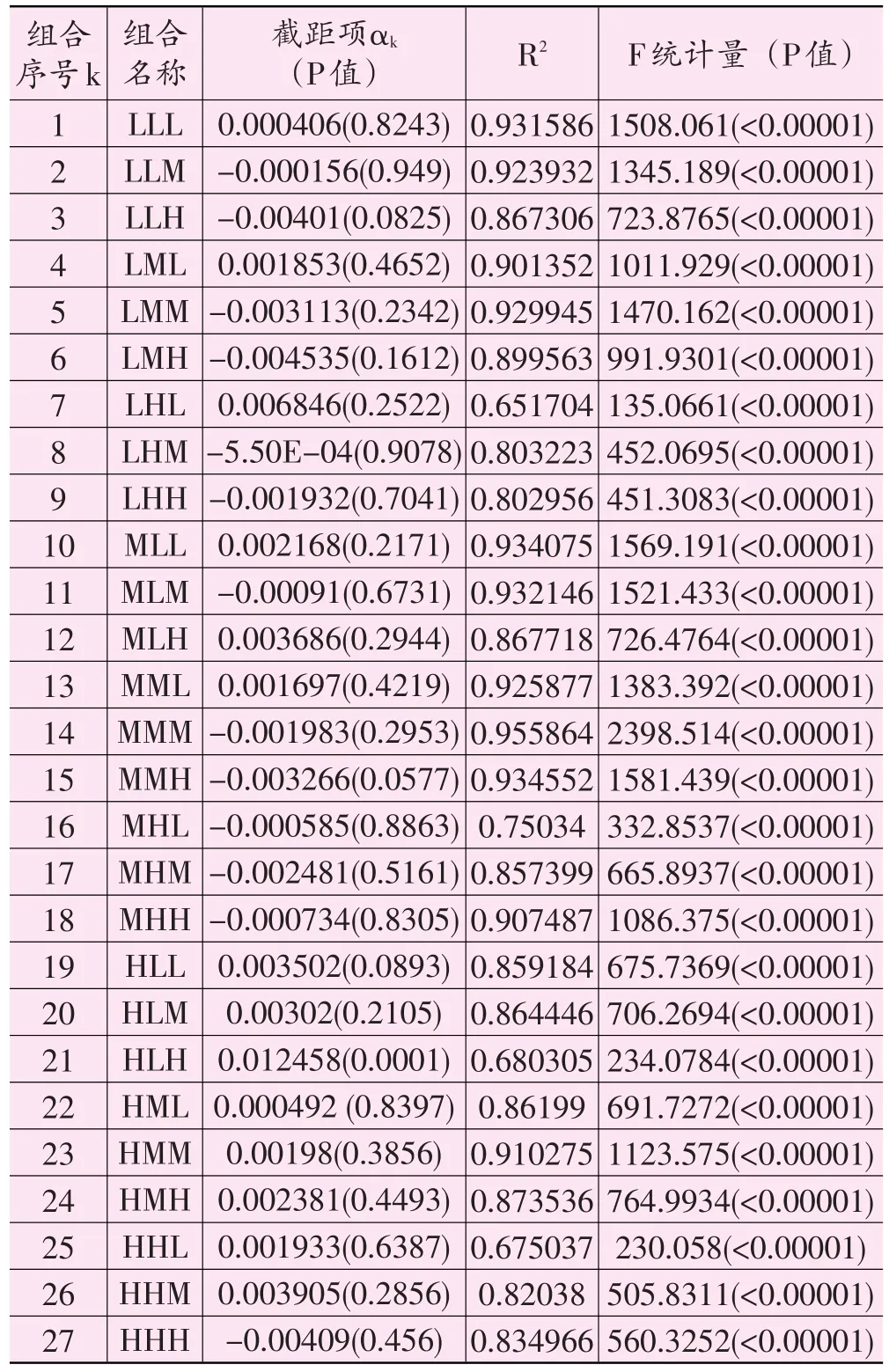
表2 基于可交易价值的资本资产定价模型时间序列回归结果

首先，从模型正确性来看，所有27个组合F统计量的P值都小于0.00001，说明模型的正确性是毋庸置疑的。

其次，从模型的拟合程度上来看，R2最小为0.651704，27个组合中，11组的R2大于0.9，23组的R2大于0.8，在余下的4组拟合程度较低的组合中，有3组是流动性高（换手率高）而波动性低的组，根据上文对27个组合日收益数据的描述统计分析，我们发现这类组合为同等价格水平下收益最高的组，也就是市场中最受关注的那部分个股的组合，而另一个拟合不够理想的组合为HLH组，即股价高，流动性差而波动性大的个股组合，直观上也是市场中表现比较极端的，因此，这几个组合的交易数据中很有可能由于存在过多的噪音而影响了模型的判断。但是，从总体上看，我们认为模型的拟合程度还是比较理想的。

再次，关于截距项，在0.05显著性水平下，其中26个组合的截距项为零，另一组截距项不为零的即为前面提到的HLH组，所以在绝大多数组合中，本文模型是能够全面解释日风险收益率的。

最后，关于可交易价值各因素的拟合系数，除上文提到的个别极端情况的组合外，其余组合的回归系数均能通过检验，系数显著的比例均高于92%（限于篇幅，有关数据不再一一列示），表明可交易价值各因素对我国沪深A股的时间序列数据具有较好的解释能力。

2.横截面回归

对时间序列回归的结果再次进行横截面回归，回归方程为（3）式：

其中，Rk-rf,k为第k组样本序列中最后一周的平均日风险收益率（未参加时间序列回归的样本点）。回归结果如表3所示。

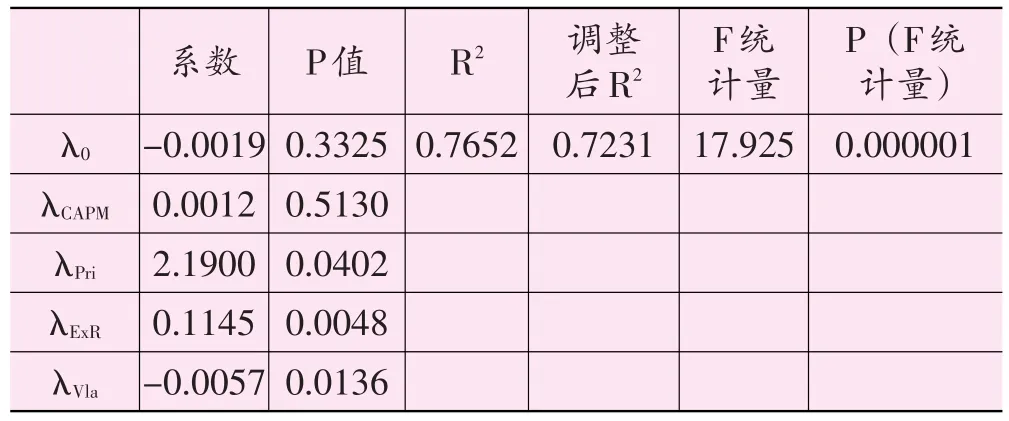
表3 基于可交易价值的资本资产定价模型横截面回归结果

首先，模型F统计量的P值接近于0，说明模型正确。R2为0.7652，调整后R2亦达到0.7231，这在横截面回归中算是比较理想的，说明模型的拟合程度较好。

其次，截距项λ0在0.1显著性水平下不显著，回归方程的截距项为0，说明模型能够全面地解释我国沪深A股的横截面日收益率。

最后，再来看模型中四个影响因子的回归系数，其中，λPri、λExR、λVla在0.05显著性水平下显著，λExR在0.01显著性水平下显著，说明价格因子、流动性因子和波动性因子对我国沪深A股的日收益率均具有解释能力，与本文前面论述的观点一致；流动性因子的解释能力最强，也与人们长期以来的理论和实践结果相符；但是系统风险因子的回归系数λCAPM对应P值为0.5130，说明其对股票横截面日收益率并不具有解释能力。从因子的影响方向上看，股票的日收益率与绝对股价和换手率正相关，但与波动性负相关，说明股票价格越高，交投越活跃，预期收益也就越高，但如果股票的波动越大，预期收益率反而越低。这样的结果与前文描述统计分析中得出的结论是完全一致的。

四、与Fama-French三因子模型的对比分析

为了对本文模型的适合性进行更全面的评估，下面我们将在同等条件下将其与著名的Fama-French三因子模型进行对比。这里，样本筛选和组合构造与上文相同，但需要单独计算每个交易日Fama-French三因子模型中HML因子和SMB因子的值。具体的，SIZEi,j为个股i在第j-1个交易日的收盘价与总股数的乘积，BMi,j则为帐面价值与SIZEi,j的比值，其中的帐面价值按每年年报和中报披露数据计算，自每年的5月第一个交易日和11月的第一个交易日开始更改。HML和SMB数据每日计算一次，分别记为HMLj和SMBj（j=1,2…448），计算方法完全与文献［13］、［14］相同。最后，分别按（4）式和（5）式进行时间序列回归和横截面回归，横截面回归结果如表4所示。

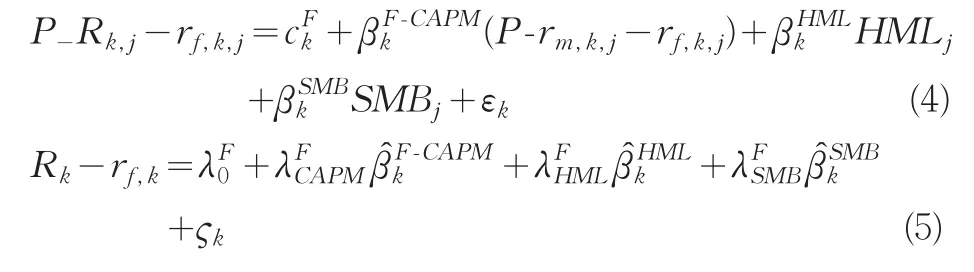
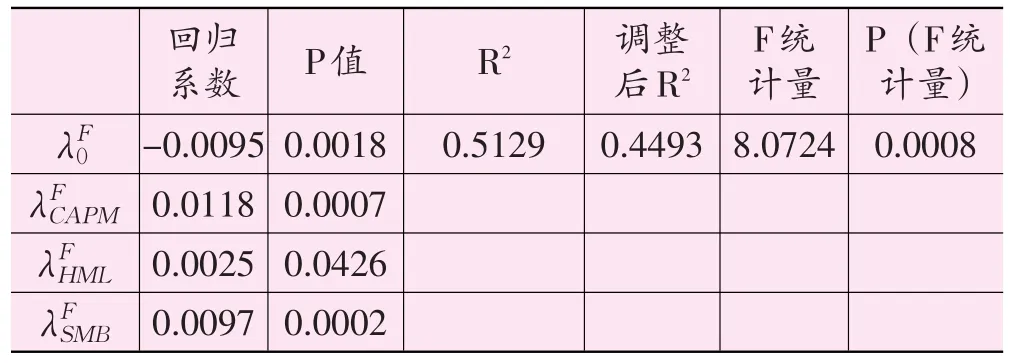
表4 Fama-French三因子模型横截面回归结果

显然，Fama-French三因子模型在本文样本数据中的表现并不理想。首先，虽然F统计量是显著的，但其值小于本文模型的结果，说明其模型的正确程度低于本文模型；其次，横截面回归的R2为0.5129，调整后的R2为0.4493，虽然表明模型具有一定的拟合能力，但表现也不如本文模型；最后，虽然市场因子、HML因子和SMB因子在0.05显著性水平下显著，说明它们都对样本数据的日横截面收益具有解释能力，但模型的截距项不为零，表明除了模型中的三个因素之外，还有其它因素没有被考虑，也就是说，Fama-French三因子模型没能全面地解释我国沪深A股的日截面收益率。

因此，我们可以认为，Fama-French三因子模型在对我国沪深A股市场股票日截面收益率的解释中表现不佳，劣于基于可交易价值的资本资产定价模型。

五、结论与展望

基于资产链的思想，本文从资本资产价格的形成过程入手，分析了以股票为代表的资本资产可交易价值的可能影响因素，并在CAPM模型的基础上，建立了基于可交易价值的资本资产定价模型，进而利用我国沪深A股市场的日交易数据对其进行了实证分析，并与Fama-French三因子模型进行了详细的对比，得出以下结论：

(1)基于可交易价值的资本资产定价模型能够全面地解释我国沪深A股市场股票的日收益率，模型正确性高，拟合程度良好。

(2)涉及股票可交易价值的股价因子、流动性因子和波动性因子均对股票日横截面风险收益具有较强的解释能力，而传统的系统风险因子却不具有解释能力。其中，以换手率为表现形式的流动性因子的影响能力最强，而长期以来不为人们所关注的股价因子和波动性因子的解释能力略弱。

(3)根据本文模型，股票的日横截面风险收益率与其股价和流动性水平正相关，而与波动性水平负相关。考虑本文样本区间内我国沪深A股市场的实际情况，这一结论是与现实相符的。

(4)基于可交易价值的资本资产定价模型无论从模型的正确性、拟合程度还是系数的解释能力来说，都优于Fama-French三因子模型，在本文的样本区间内，Fama-French三因子模型甚至不能对相关的日收益率做出全面的解释。因此，相对于传统的主要以月度收益为对象的中长期收益行为研究而言，以日收益为代表的短期收益率与本文提出的可交易价值息息相关。

［1］ 吴冲锋，王柱，冯芸.基于资产链的资产定价问题的思考［J］.管理科学学报，2008，(1):1-11.

［2］ 张普，吴冲锋.基于非参数蒙特卡罗模拟的股票波动性价值研究［J］.管理科学，2009，(3):89-95.

［3］ Anshuman V R,Kalay A.Can Splits Create Market Liquidity?Theory and Evidence［J］.Journal of Financial Markets,2002,5:83-125.

［4］ Dennis P.Stock Splits and Liquidity:the Case of the Nasdaq-100 Index Tracking Stock［J］.Financial Review,2003,38:415-433.

［5］ Mohanty S,Moon D.Disentangling the Signaling and Liquidity Effects of Stock Splits［J］.Applied Financial Economics,2007,17:979-987.

［6］ Longstaff F A.How Much Can Marketability affect Security Values［J］.Journal of Finance,1995,50:1767-1774.

［7］ Longstaff F A.Placing No arbitrage Bounds on the value of Nonmarketable and Thinly Traded Securities［J］.Advances in Futures and Options Research,1995,8:203-228.

［8］ Acharya A A,Pedersen L H.Asset Pricing with Liquidity Risk［J］.Journal of Financial Economics,2005,77:375-410.

［9］ Amihud Y,Mendelson H,Pedersen L H.Liquidity and Asset Prices［J］.Foundations and Trends in Finance,2005,1:269-364.

［10］ 陈雨露,汪昌云.金融学文献通论——微观金融卷［M］.北京：中国人民大学出版社，2006：178-210.

［11］ Ang A,Robert H,Xing Y,et al.The Cross Section of Volatility and Expected Returns［J］.Journal of Finance,2006,61:259-299.

［12］ Adrian T,Rosenberg J.Stock Returns and Volatility:Pricing the Short-run and Long-run Components of Market Risk［J］.Journal of Finance,2008,63:2997-3030.

［13］ Fama E F,French K R.The Cross Section of Expected Stock Returns［J］.Journal of Finance,1992,47:427-465.

［14］ Fama E F,French K R.Common Risk Factors in the Returns on Stocks and Bonds［J］.Journal of Financial Economics,1993,33:3-56.