基于模糊控制的双馈风力发电功率解耦研究

陈天立，刘相华，贾文强，康忠健

（1.中国核电工程有限公司 郑州分公司，河南 郑州 450052；2.垦利县供电公司，山东 东营 257500；3.中国石油大学（华东）电气工程系，山东 东营 257061）

1 引言

双馈风力发电变速恒频系统在风力发电系统中得到广泛应用，基于定子磁链矢量控制简化电机模型，由于要观测定子磁链，增加了控制系统的复杂性，本文采用基于定子电压定向的矢量控制，省去了定子磁链观测器［1］。

模糊逻辑控制是一种新颖的控制策略，无论是在非线性还是多变量系统中，特别是当数学模型未知或不确定时，都能产生令人满意的效果［2］。而由于空气动力学的不确定性和电力电子模型的复杂性以及其他诸如老化和大气条件等因素都会引起电机参数的变化，导致传统PI控制策略性能变差。本文在采用基于定子电压定向的矢量控制简化双馈发电机数学模型的基础上，将模糊控制技术引入双馈风力发电系统有功功率和无功功率解耦控制中，不仅实现了最大风能捕获，而且提高了风力发电系统的运行性能。

2 双馈风力发电机模型［1，3－5］

规定定、转子绕组均采用电动机惯例，即向绕组方向看时，电压降的正方向与绕组电流的正方向一致，电流与磁链符合右手螺旋法则。采用定子电压定向下d－q坐标系下双馈发电机磁链和电压模型分别为

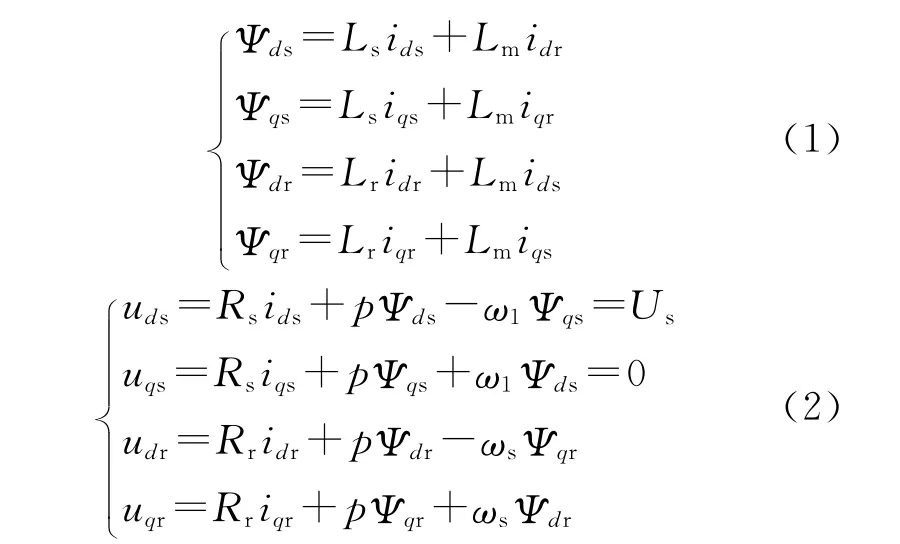
式中：u，i，Ψ 分别为电压、电流、磁链；R，L分别为电阻和自感；下标的d，q为d－q轴分量；下标s，r为定转子分量；Lm为互感；ω1为同步电角速度；ωs为d，q坐标系相对于转子的电角速度，即为转差的电角速度，ωs＝ω1－ωr，ωr为转子电角速度。

在忽略定子电阻后，根据式（1）和式（2）将双馈发电机磁链和电压数学模型可分别简化为

定子有功功率和无功功率方程为

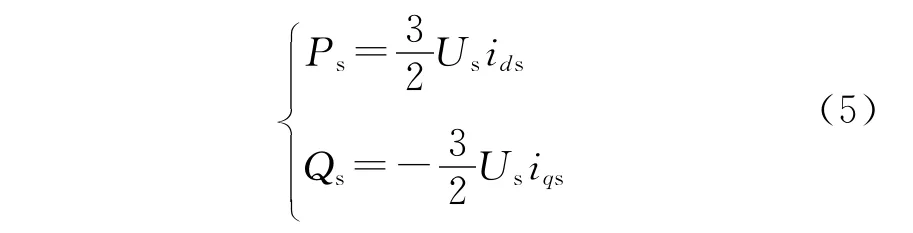
从式（5）中可知，因为定子直接连接电网，所以Us为恒定值，有功和无功与定子电流的q轴和d轴分量线性关系。有功无功的控制可以解耦为定子电流的d轴和q轴的控制。控制的实现是采用控制转子电压来实现的。

3 DFIG 最大风能捕获控制［6－11］

根据贝兹理论，风力机产生的机械功率为

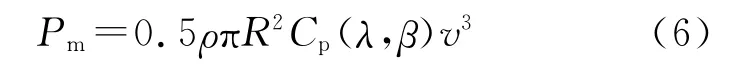
式中：ρ为空气密度；R为风力机风轮半径；Cp为风能转换系数；λ为叶尖速比；β为桨叶节距角；v为风速。

其中叶尖速比λ是叶尖线速度与风速之比的函数，如下：

式中：ωm为风轮旋转的机械角速度，rad／s。

在β一定时，典型的Cp与λ之间的关系曲线示意图如图1所示。

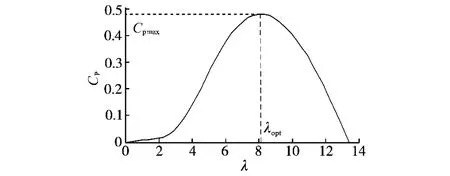
图1 风力机叶尖速比和风能转换系数之间的关系曲线Fig.1 Relation curve of tip－speed ratio and wind energy utilization factor of wind turbine

由图1可知，在任何风速下，只要调节风力机转速，使其叶尖线速度与风速之比λ保持不变，且都满足λ＝λopt，就可维持风力机在Cpmax运行。根据式（6）和式（7），可得风力机输出机械功率和机械角速度的关系曲线，如图2所示。

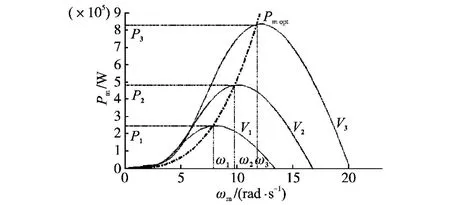
图2 风力机输出机械功率和机械角速度的关系曲线Fig.2 Relation curves of output mechanical power and mechanical angular velocity of wind turbine

由图2可以得到风力机输出机械功率的最佳曲线Pmopt，要使风力机运行在这条曲线上，必须在风速变化时及时调节转速，保证最佳叶尖速比，风力机将会获得最大风能捕获，有最大机械功率输出：

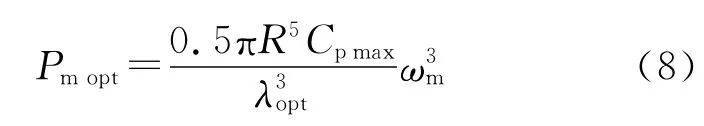
额定风速以下，双馈发电机次同步运行，有以下功率关系：

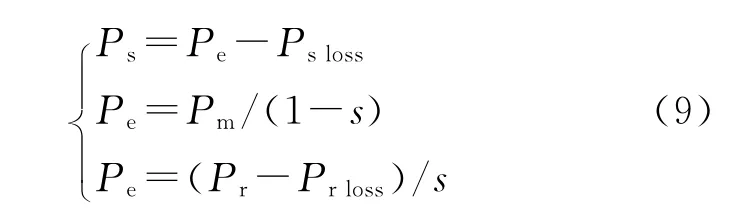
式中：Pe为电磁功率；Psloss为定子铜耗及电机铁耗；Pr为转子吸收的有功功率；Prloss为转子铜耗；s为转差率。

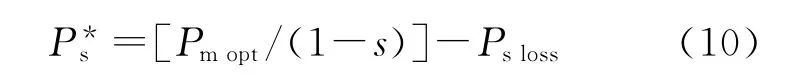
4 功率解耦模糊控制器的设计

本文采用参数自整定模糊PI控制器。为了满足对PI控制器参数自整定的要求，利用模糊控制规则在线对PI的比例和积分进行修改。其模糊PI控制器系统框图如图3所示。

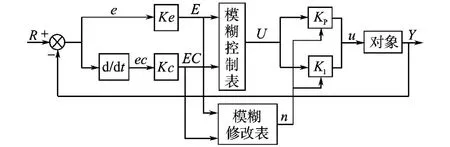
图3 参数自整定模糊PI控制器系统框图Fig.3 System block diagram of the parameter self－tuning fuzzy PI controller

参数自整定的基本思想［12］是：当偏差或偏差变化率ec较大时，进行“粗调”，即放大KP，KI；当偏差e或偏差变化率ec较小时，进行“细调”，即缩小KP，KI；放大倍数的语言变量N 为下列词集：N＝｛AB，AM，AS，OK，CS，CM，CB｝。

这里AB，AM，AS，OK，CS，CM，CB 分别表示高放，中放，低放，不变，小缩，中缩，大缩的模糊子集，N 的论域规定：｛0.125，0.25，0.5，1.0，2.0，4.0，8.0｝。

在一控制周期内的参数自整定模糊PI控制器系统流程如图4所示。

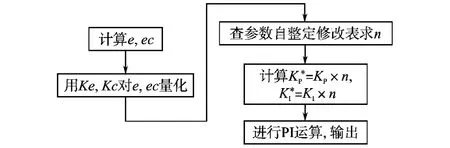
图4 参数自整定模糊PI控制器系统流程Fig.4 Control flow of parameter self－tuning fuzzy PI controller

系统整体控制框图如图5所示。对于功率解耦控制，首先检测电网三相电压uabcs、三相定子电流iabcs和三相转子电流iabcr，用锁相环（PLL）获得电网电压矢量相位θ1和同步转速ω1。利用光电编码求得转子角速度ωr，从而求得转子位置角θr。根据式（5）求得定子有功功率Ps和无功功率Qs，定子有功功率给定由式（10）可计算得出，定子无功功率给定设置为0，实现单功率因数，分别作为模糊PI控制器的输入，得到转子电流的d轴分量给定i＊dr和q轴分量给定，并通过模糊PI控制器和式（4）得到转子电压的q轴分量和d轴分量，经旋转变换生成SVPWM，实现对双馈电机的转子侧变换器的控制，最终实现双馈电机的功率解耦控制。

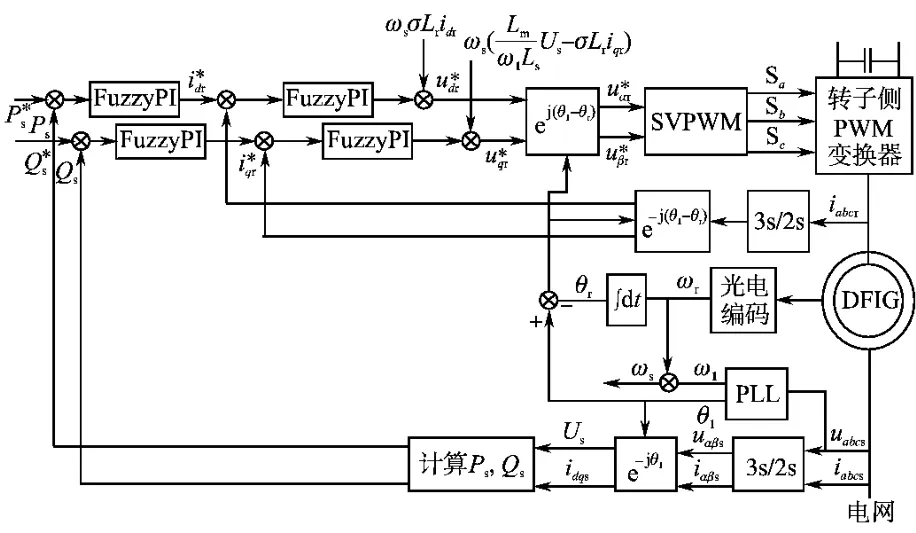
图5 系统整体控制框图Fig.5 Block diagram of whole system control

5 仿真结果

本文采用 Matlab／Simulink为实验平台，根据各个部分数学模型公式，建立了各部分数学模型并进行仿真，系统仿真模型如图6所示。电机参数为：额定电压380V，额定功率20kW，定子电阻Rs＝3.74Ω，定子漏感Ls＝0.3042H，转子电阻Rr＝3.184Ω；转子漏感Lr＝0.3107H，互感Lm＝0.2920H，极对数p＝2，转动惯量J＝0.1kg·m2。

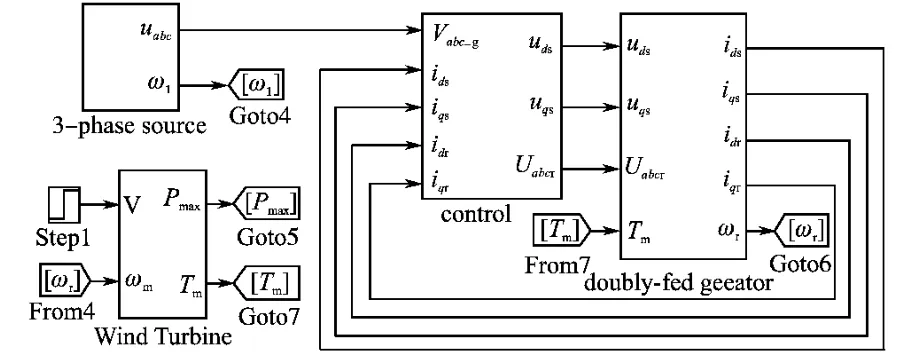
图6 功率解耦系统仿真模型Fig.6 Simulation model of power decoupling control

1）当风速为12m／s，无功功率给定为0，且电机参数恒定时对系统进行仿真，波形如图7所示。

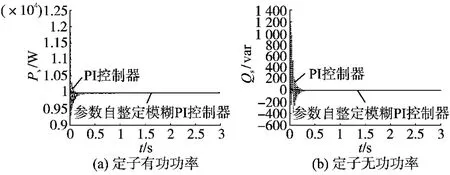
图7 风速为12m／s时的仿真波形Fig.7 Simulation waveforms when the wind speed is 12m／s

由图7a可得，与PI控制相比，模糊PI控制能够更快地调节定子侧有功功率获得最优功率。将无功功率给定设置为0，由图7b可得，与PI控制相比，模糊PI控制能够更快地调节定子侧无功功率为0，获得单位功率因数。

2）当风速在1s由12m／s变化为14m／s，无功功率给定为0，且电机参数恒定时对系统进行仿真，波形如图8所示。

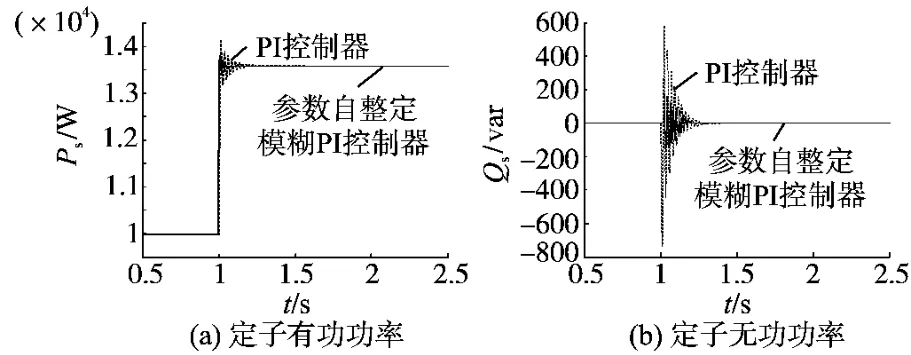
图8 风速变化时的仿真波形Fig.8 Simulation waveforms when the wind speed is variable

由图8a可得，当风速改变时，与PI控制相比，模糊PI控制能够更快地调节定子侧有功功率，根据风速的变化相应地改变到对应的最佳功率。将无功功率给定设置为0，由图8b可得，当风速变化时，与PI控制相比，模糊PI控制能够更快地调节定子侧无功功率为0，获得单位功率因数。

3）当风速不变时，无功功率给定为3800var，在0.5s时电机转子电阻变为原来的1.5倍，对系统进行仿真，波形如图9所示。

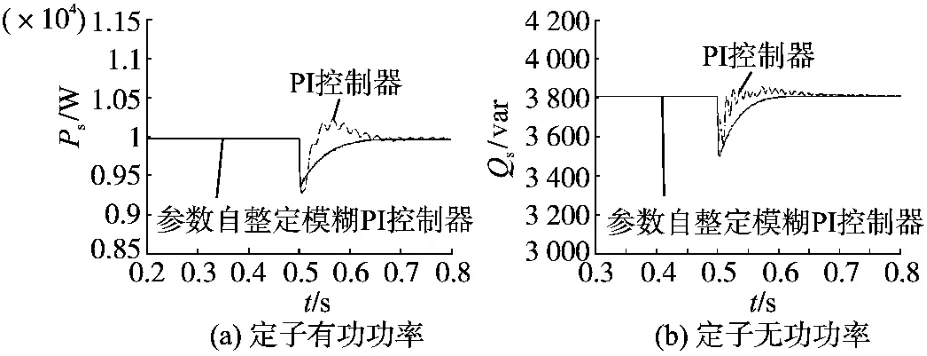
图9 风速不变时的仿真波形Fig.9 Simulation waveforms when the wind speed is unvariable

由图9a可得，当电机参数变化时，与PI控制相比，模糊PI控制能够更快地调节定子侧有功功率获得对应的最佳功率；由图9b可得，与将无功功率给定设置为3800var，当电机参数变化时，与PI控制相比，模糊PI控制能够更快地调节定子侧无功功率到给定值。

6 结论

本文对通过变速恒频风力发电系统进行分析，在采用基于定子电压定向的矢量控制简化双馈发电机数学模型的基础上，将模糊控制技术引入双馈风力发电系统有功功率和无功功率解耦控制中，不仅实现了最大风能捕获，而且提高了风力发电系统的运行性能。仿真结果验证了自适应模糊PI控制器与PI控制器相比，依靠模糊控制器的自调整能力能够实时在线地按照系统的偏差对控制器参数进行调整，大大减弱了对电机参数准确性的依赖程度，从而提高了控制器的自适应能力和鲁棒性。

［1］赵仁德.变速恒频双馈风力发电机交流励磁电源研究［D］.杭州：浙江大学，2005.

［2］刘金琨.先进PID控制及其 MATLAB仿真［M］.北京：电子工业出版社，2003.

［3］Krause P C.Analysis of Electric Machinery［M］.McGraw－Hill，1986.

［4］Pablo Ledesma，Julio Usaola.Effect of Neglecting Stator Transients in Doubly Fed Induction Generators Models［J］.IEEE Trans.on Energy Conversion，2004，19（2）：459－461.

［5］Ekanayake J B，Holdsworth L，Jenkins N.Comparison of 5th Order and 3rd Order Machine Models for Doubly Fed Induction Generator（DFIG）Wind Turbines［J］.Electric Power Systems Research，2003，67（3）：207－215.

［6］王志华，李亚西，赵栋利，等.变速恒频风力发电机最大功率跟踪控制策略的研究［J］.可再生能源，2005（2）：16－19.

［7］Ming Yini，LI Gengyin，ZHOU Ming.Analysis and Comparison of Dynamic Models for the Doubly Fed Induction Generator Wind Turbine［J］.电力系统自动化，2006，30（13）：22－27.

［8］黄科元，贺益康，卞松江.矩阵式变换器交流励磁的变速恒频风力发电系统的研究［J］.中国电机工程学报，2002，22（11）：100－105.

［9］Jovanovic M G，Betz R E.Power Factor Control Using Brushless Doubly Fed Reluctance Machines［C］∥In：Industry Applications Conference，2000.Conference Record of the 2000IEEE，2000（1）：523－530.

［10］陆城，许洪华.风力发电用双馈感应发电机控制策略的研究［J］.太阳能学报，2004，25（5）：606－611.

［11］淡军，孙茂相，杨继华.风电系统最大功率捕获的研究［J］.沈阳工业大学学报，2003，25（1）：40－42.