风电机组MPPT动态功率曲线控制策略的研究

夏安俊，胡书举，许洪华

（1.中国科学院 电工研究所，北京 100190；2.中国科学院 研究生院，北京 100049；3.中国科学院 风能利用重点实验室，北京 100190）

1 引言

变速运行的风力发电机组其转速可以随着风速的变化而变化，因而能够最大限度地捕获风能，拥有恒速风力发电机组所不具备的对最大功率点跟踪的能力。

在额定风速以下如何最大化风能的利用率，即对最大功率点的跟踪（MPPT）控制是变速运行风电机组的主要任务之一。目前关于最大功率点跟踪的问题已经提出了很多控制算法，如：叶尖速比法［1－2］通过调节机组转速将叶尖速比维持在一个最佳值上，但是需要预先知道最佳叶尖速比值和测量风速，从而增加了成本以及算法实际执行的难度，同时控制精度难以保证；功率信号反馈法（功率曲线法）［3－4］需要预先得到机组的最大功率曲线，从而增加了算法实际执行的难度，同时随着使用年限的增加，机组特性的变化，控制精度也难以保证；登山搜索法（HCS）［5－7］在风速不变的情况下控制效果较好，但是在风速有波动的情况下无法对系统进行有效的控制。3种比较法［8］虽然简单，易于操作，但是在随机风速下会给取点带来误差，引起误操作，给实际工作带来了困难。

针对上述情况，本文提出了一种基于模糊控制理论的MPPT动态功率曲线控制策略，在整个控制过程中，控制系统根据机组的实际运行状态点与最大功率点之间的位置关系和相应的变化趋势来调节功率曲线的系数，以达到对机组最大功率点跟踪控制的目的。该控制策略的优点是：对机组的参数依赖性较小，可移植性强，在外界气温变化和机组参数老化以及机组转速测量出现偏差的情况下，都可以自动跟踪到相应风速的最大功率点上，实现机组最大功率点的跟踪控制。

2 最大功率点功率曲线控制原理

处于额定风速以下（桨距角为0°时）的风力发电机组机械功率与风轮转速以及最大功率曲线的关系曲线如图1所示。

图1 机械功率与风轮转速及最大功率曲线Fig.1 Turbine′s mechanical power－rotor speed and maximum power curves

在不同的风速下都有一个最优转速值使得风力发电机组捕获的机械功率达到最大值，即当风力发电机组的风轮转速为该特定值机组捕获到的最大风能。不同风速下的最大功率点的连线即为最大功率曲线，因此必须控制风轮转速以保证风力发电机组始终运行在最优转速点，或者在风速变化的情况下处于对最优转速点的跟踪状态，以实现风力发电机组的最大功率点跟踪控制的目的。

风电机组机械功率与风速的关系式［5］：

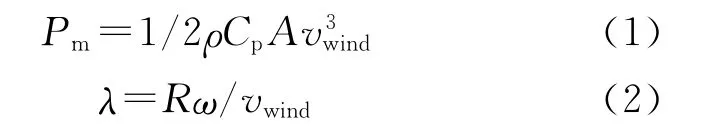
将式（2）代入式（1）得：

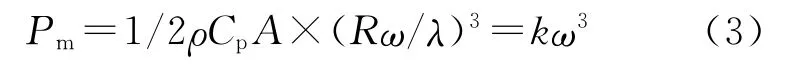
其中

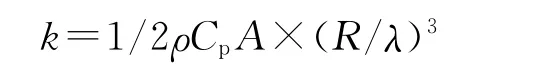
式中：Pm为机组的机械功率；ρ为空气密度；Cp为风能利用系数；A为风轮的旋转扫风面积；vwind为当前风速；λ为叶尖速比；ω为风轮转速（此处用角速度表示）；R为风轮半径；k为比例系数（是机械功率除以转速3次方的值）。

理想情况下，不同风速下的最大功率点组成的曲线（称为最大功率曲线）与风轮转速近似成3次方的关系。

对于1台风力发电机组来说，有一条比例系数k固定不变的最大功率曲线，如图1所示。

实际运行的机组一般采用这种固定的功率曲线或者等价的转速与功率（或者转矩）查找表来控制机组的转速即根据当前机组的转速通过功率曲线或者查找表得出机组功率的给定值，用来控制机组的输出功率。当实际机组的功率大于此给定值时，机组就会自动加速，小于此给定值时，机组就会自动减速，从而实现机组最大功率点的跟踪控制。但是根据图1中的最大功率曲线与不同风速下的功率曲线的关系，可以看出实际运行状态点越接近最大功率点，机组的给定功率与实际功率的误差就越小，对最大功率点的跟踪速度就会变慢。同时当外界的气温变化，以及随着使用年限的增加，机组的参数出现变化时，这种控制方式无法做出有效的响应，所以难以保证机组始终具有最大功率点跟踪的能力。

因此，本文提出了机组最大功率点的动态功率曲线跟踪策略，以解决上述问题。

3 最大功率点动态功率曲线跟踪策略

动态功率曲线跟踪策略：首先构造一条功率曲线，功率与转速的关系如式（3）所示，然后根据机组的运行状态点与最大功率点的位置关系和变化趋势来调节式（3）中的比例系数k；测量出当前机组的转速，然后通过功率曲线得出对应于此转速的机械功率值，并作为机组的机械功率的给定值用来控制机组的转速，实现对最大功率点的跟踪控制。

其中，比例系数k的初始值设定尽量靠近最大功率曲线的系数以减小系统的初始调节时间，因为比例系数k基本在最大功率曲线的系数附近变化。由于比例系数k在控制过程中是变化的，所以功率曲线是动态的。

由图2可以看出，比例系数k的值越大，功率曲线的交点对应的转速就越小；比例系数k的值越小，功率曲线的交点对应的转速就越大；因此，通过改变比例系数k值的大小就可以调节实际机组机械功率与给定功率之间的误差值的大小，从而可以对机组跟踪最大功率点的速度进行控制，即误差值越大，跟踪速度越快。

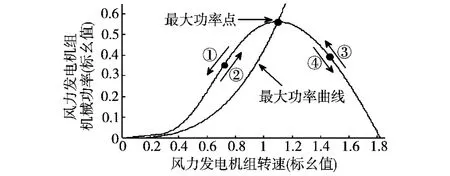
图2 机组运行状态点的变化趋势Fig.2 The trend of machine′s operating state point

对比例系数k值的调节具体步骤如下。

首先求出机组机械功率对转速的导数dPm／dω和转速对时间的导数dω／dt，然后根据两者之间的关系判断机组实际运行状态点的变化趋势，并对比例系数k值进行相应的调节。

1）当dPm／dω＞0且dω／dt＜0，机组实际运行状态点在最大功率点的左侧，且随着时间的增加，转速逐渐减小，此时，机组有偏离最大功率点的变化趋势，如图2的①所示。为了实现对机组最大功率点跟踪的目的，需要增加机组的转速，以改变实际运行状态点偏离最大功率点的变化趋势；因此，通过降低比例系数k，增加机组的给定功率与实际功率的差值，以改变实际运行状态点的变化趋势，使其向最大功率点靠近。

2）当dPm／dω＞0且dω／dt＞0，机组实际运行状态点在最大功率点的左侧，且随着时间的增加，转速逐渐增大，此时，机组有靠近最大功率点的变化趋势，如图2的②所示。可以进一步增加转速使机组的实际运行状态点向最大功率点靠近。因此，通过降低比例系数k，增加机组的给定功率与实际功率的差值，以提高实际运行状态点向最大功率点靠近的速度。

3）当dPm／dω＜0且dω／dt＜0，机组实际运行状态点在最大功率点的右侧，且随着时间的增加，转速逐渐减小，此时，机组有靠近最大功率点的变化趋势，如图2的③所示。可以进一步减小转速使机组的实际运行状态点向最大功率点靠近。因此，通过升高比例系数k，增加机组的给定功率与实际功率的差值，以提高实际运行状态点向最大功率点靠近的速度。

4）当dPm／dω＜0且dω／dt＞0，机组实际运行状态点在最大功率点的右侧，且随着时间的增加，转速逐渐增加，此时，机组有偏离最大功率点的运行趋势，如图2的④所示。为了实现对机组最大功率点跟踪的目的，需要增加机组的转速，以改变实际运行状态点偏离最大功率点的变化趋势；因此，通过升高比例系数k，增加机组的给定功率与实际功率的差值，以改变实际运行状态点的变化趋势，使其向最大功率点靠近。

4 最大功率点动态功率曲线模糊控制方案的设计

上文提出的最大功率点的动态功率曲线跟踪策略，具有强非线性特性。而近代控制理论中的模糊控制技术在处理非线性和控制具有高度不确定性的复杂系统时有着突出的优越性。因此本文选用了模糊控制技术来设计上文提出的最大功率点的跟踪控制方案。

模糊控制器根据机械功率对转速的导数dPm／dω和转速对时间的导数dω／dt的大小判断机组的实际运行状态并对比例系数k进行增量式修改，即控制的输出通过一个积分环节，作为偏移量加到比例系数k上。

设计的模糊控制器为二输入一输出型，输入分别为dPm／dω和dω／dt，输出为增量Δk。

为了方便起见，输入都采用论域为［－6，6］的三角形隶属函数，输出采用论域为［－4，4］的三角形隶属函数。

模糊子集的设计如下。

输入模糊集论域：“正大”（PL）：［3，6，9］，“正小”（PS）：［0，3，6］，“零”（ZO）：［－3，0，3］，“负小”（NS）：［－6，－3，0］，“负大”（NL）：［－9，－6，－3］。

输出模糊集论域：“正大”（PL）：［2，4，6］，“正小”（PS）：［0，2，4］，“零”（ZO）：［－2，0，2］，“负小”（NS）：［－4，－2，0］，“负大”（NL）：［－6，－4，－2］。

采用Mamdani控制规则并根据最大功率点动态功率曲线跟踪策略，设计模糊控制规则，即If dPm／dωis NLand dω／dt is NLthenΔkis PL，类似的可得模糊控制规则表如表1所示 。

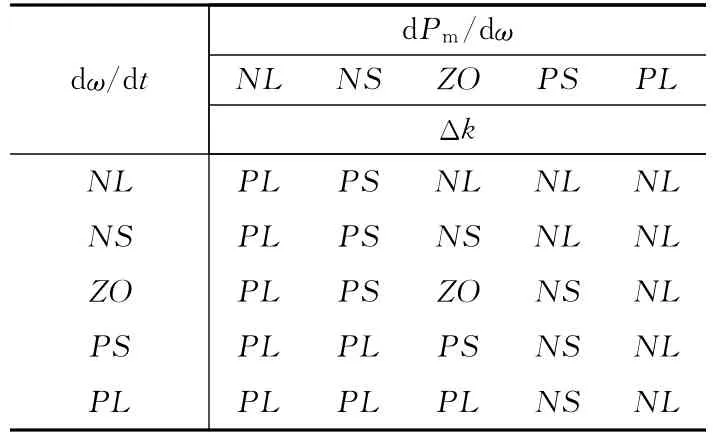
表1 模糊控制的规则表Tab.1 Rule for fuzzy control

模糊推理采用Mamdani极小运算法，合成方式采用极大极小运算。输出采用重心法解模糊。

输入量需要乘以相应的输入量化因子，以调节控制器对输入量的敏感度。输入量化因子选得越大，系统对输入量的敏感度就越高，映射到输入论域“零”的实际输入量范围就越小，输入量的控制作用就越大；但会导致超调量的增加及过渡过程的延长。因此输入量化因子的大小对系统动态性能影响很大，需要根据系统的特性作出适当的选择。

输出量需要乘以相应的输出量化因子，以调节输出量对系统的影响程度。输出量化因子如果选得大，功率曲线变化速度快，选得小，功率曲线变化速度就慢，具体值可根据所要求的功率曲线变化速度来定。

5 仿真结果

根据上述设计了模糊控制方案，应用Matlab仿真软件构建变速运行风力发电机组仿真系统。其中转速和机械功率都采用了标幺值的表示方式（机组的额定功率为1.5MW，同步转速为1800 r／min）。按照图1的转速与机械功率的关系设计机组的功率特性，即风速3m／s至12m／s的最大功率点所对应的最优转速分别是0.4，0.5，0.6，0.7，0.8，0.9，1，1.1。

仿真系统中，机组的初始转速设为1（标幺值）；功率曲线的比例系数k初始值设为0.0946；对于输入信号dPm／dω，选择量化因子为30，即将｜dPm／dω｜＜0.1的区域映射为模糊论域的“零”（ZO）；对于输入信号dω／dt，选择量化因子为1，即将｜dω／dt｜＜3的区域映射为模糊论域的“零”（ZO）；对于输出信号Δk，选择量化因子为0.0001。

5.1 机组转速测量出现偏差时的跟踪情况

风速初始值为8m／s，在150s时跃变为10 m／s。

图3中的曲线①②③分别是测量转速的偏差为0（标幺值），＋0.02（标幺值），－0.02（标幺值）时，动态功率曲线比例系数的变化情况，图4中的曲线①②③分别是3种情况下机组对最大功率点跟踪的转速波形图。

根据动态功率曲线控制原理可知：在风速一定时，若最优转速为ω1，相应的最大功率点的功率值为P1，相应的比例系数为k1，由式（3）可知：

图3 比例系数k的变化Fig.3 The change of the proportion coefficient k

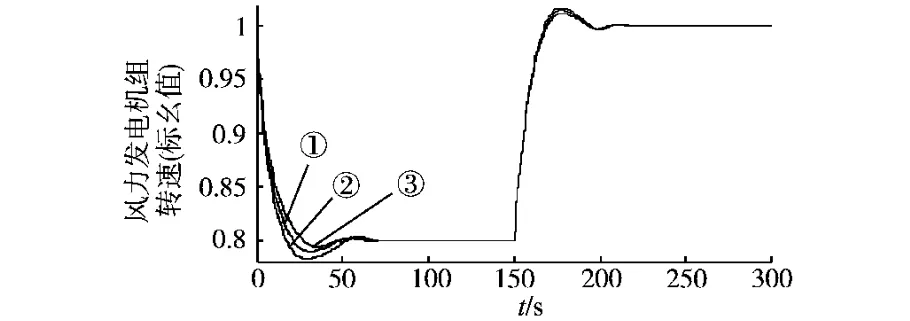
图4 机组转速Fig.4 Turbine′s rotor speed

当测量的转速出现偏差时，即实际机组最优转速为ω1，而测量转速为ω1＋Δω时，机组要跟踪到最大功率点，功率曲线的比例系数必须为k＝P1／（ω1＋Δω）3，因此，当Δω＞0时，k将会偏小；Δω＜0时，k将会偏大。

由图3的曲线①②可以看出，测量转速偏差为正（如0.02标幺值）时，相应功率曲线的比例系数在最大功率点处的值要小于测量转速无偏差时比例系数的值；由图3的曲线①③可以看出，测量转速偏差为负（如－0.02标幺值）时，相应功率曲线的比例系数在最大功率点处的值要大于测量转速无偏差时比例系数的值。仿真结果符合MPPT动态功率曲线控制的理论分析。

由图4可以看出，在测量转速出现偏差的情况下，动态功率曲线控制策略可以控制机组跟踪到相应的最优转速上，而且不受转速测量偏差的影响。

5.2 风速存在随机波动时的跟踪情况

风速的初始值为6m／s，在600s时跃变为8 m／s；且叠加有±2m／s随机波动风速（随机波动时间间隔为0.5s）。

图5和图6分别是相应的机组转速和比例系数k的变化波形。可以看出，在随机波动的风速下，机组的转速和比例系数k基本稳定在相应的基准值上。因此，动态功率曲线控制策略在风速出现随机波动的情况下，可以跟踪到基频风速的最大功率点。

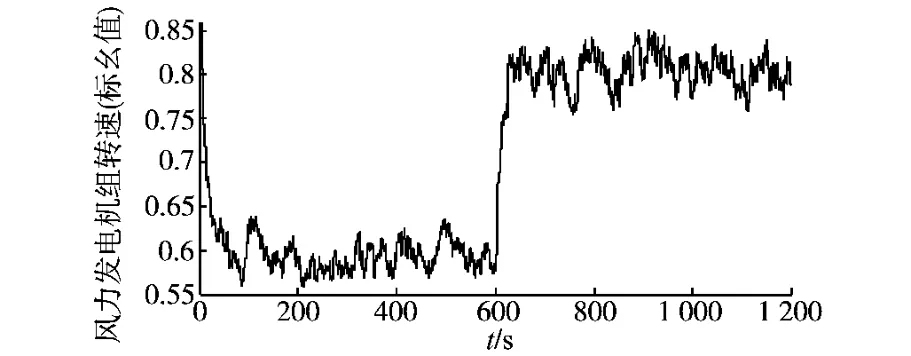
图5 机组的转速Fig.5 Turbine′s rotor speed

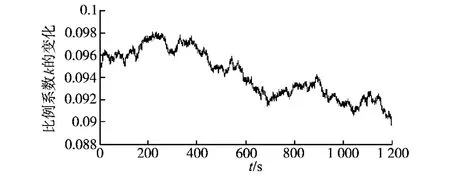
图6 比例系数k的变化Fig.6 The change of the proportion coefficient k

6 结论

本文提出的最大功率点动态功率曲线控制策略对机组的特性依赖性小，在跟踪过程中不需要测量风速，且在转速测量出现偏差的情况下，可以实现对最大功率点的跟踪控制，在风速出现随机波动的情况下，可以跟踪到基频风速的最大功率点。上述的仿真结果证明了本控制策略的正确性和有效性。

［1］Cardenas R，Pena R.Sensorless Vector Control of Induction Machines for Variable－speed Wind Energy Applications［J］.IEEE Transactions on Energy Conversion，2004，19（1）：196－205.

［2］Moor G，Beukes H .Power Point Trackers for Wind Turbines［C］∥Power Electronics Specialist Conference （PESC），2004：2044－2049.

［3］Liu Qihui，He Yikang，Zhao Rende.The Maximal Windenergy Tracking Control of a Variable－speed Constant－frequency Wind－power Generation System［J］.Automation of Electric Power Systems，2003，27（20）：62－67.

［4］Kim S，Kim E.PSCAD／EMTDC－based Modeling and Analysis of a Gearless Variable Speed Wind Turbine［J］.IEEE Trans.on Energy Conversion，2007，22（2）：421－430.

［5］Koutroulis E，Kalaitzakis K.Design of a Maximum Power Tracking System for Wind－energy－conversion Applications［J］.IEEE Trans.on Industrial Electronics，2006，53（2）：486－494.

［6］Chen Y，Liu Y，Hung S，et al.Multi－input Inverter for Grid－connected Hybrid PV／Wind Power System［J］.IEEE Trans.on Power Electronics，2007，22（3）：1070－1077.

［7］Femia N，Granozio D，Petrone G，et al.Predictive ＆ Adaptive MPPT Perturb and Observe Method［J］.IEEE Transactions on Aerospace and Electronic Systems，2007，43（3）：934－950.

［8］龙腾飞，丁宣浩，蔡如华.MPPT的三点比较法与登山法比较分析［J］.大众科技，2007，8（2）：48－50，74.