瞬态工况下无级变速车辆的功率补偿控制＊

郝允志，孙冬野，秦大同，林歆悠，尹燕莉

（1.重庆大学 机械传动国家重点实验室，重庆 400030；2.西南大学 智能传动工程技术研究中心，重庆 400715）

无级变速器（Continuously Variable Transmission，CVT）在换挡过程中不中断动力，速比连续变化，本质上可以实现平顺的换挡过程.然而因速比变化率和飞轮惯性而产生的附加转矩会影响传动系统的有效输出功率，降低车辆的动力性和舒适性[1]，尤其是急加速过程中出现的动力疲软是影响市场对CVT车辆接受程度的一个重要原因[2－3].

为消除附加转矩造成的影响，目前的研究可归纳为改进机械结构和优化控制方法两个方面.ALEX等[4]提出了零惯量CVT结构，通过增加助力飞轮和行星机构对附加转矩进行补偿，取得良好的控制效果，但由于成本、体积和重量等原因，尚未得到推广.刘金刚、邹乃威等[5－6]优化了速比控制算法，为提高瞬态工况性能提供了有利条件.PFIFFNER、张树培等[7－8]分别利用 DIRCOL工具和建模仿真对瞬态工况控制过程进行优化，提高了经济性和动力性.LEE、KIM、邓涛等[9－12]考虑传动效率、系统响应滞后和功率储备等因素，提出对发动机和CVT进行集成控制，设计了τ算法、转矩补偿算法和转速补偿算法.罗勇[13]根据车辆传动系统的力平衡关系计算最大允许速比变化率，将参数统计和模糊控制相结合，提出了综合控制策略.上述针对附加转矩的控制方法中，速比变化率均以良好平路状态的行驶阻力为依据[12－13]，依赖于车辆和路况信息，不具备普遍适用性.

本文通过对CVT瞬态工况特性和现有控制方法的分析，提出了基于有效功率的通用补偿控制方法.直接以变速器输入功率作为控制目标，克服现有控制方法依赖于车辆及路况信息的缺陷，通过分层次量化补偿功率，将控制方法划分为功率维持、零功率、增加后备功率和综合模式等4种控制模式.仿真和试验结果证明了该控制方法的可行性和通用性.

1 瞬态工况特性与新方法的提出

1.1 瞬态工况特性

在进行动力学分析时，通常将CVT传动系统简化为双旋转质量模型[1]，如图1所示.

图1 CVT传动系统结构简图Fig.1 Sketch of CVT

传动系统动力学方程为：

式中Te为发动机转矩，Tv为车辆行驶阻力换算至CVT输出端的阻力距，ωe为发动机角速度，ωv为CVT输出端角速度，Ie为发动机、飞轮等位于CVT输入端部件的旋转惯量，Iv为整车平动惯量及CVT从动轮至车轮的旋转惯量换算至CVT输出端的旋转惯量，i为速比，η为传动效率.发动机转速与车速的关系为ωe＝iωv，微分可得：

代入式（1）整理得：

式（3）表明，速比变化率对车辆加速度具有反作用，由速比变化而引起的转矩称为附加转矩Tx：

附加转矩在速比增大时为阻力矩，在速比减小时则为驱动力矩.车辆急加速时，目标速比快速增大，若对速比控制不加限制必然产生较大的速比变化率，附加转矩增大有可能造成车辆减速，违背驾驶员的操作意图.

1.2 白箱控制法与灰箱控制法

为消除附加转矩造成的影响，通常需要利用发动机后备转矩进行补偿，同时对速比变化率进行限制[9－13].由于发动机后备转矩的补偿作用有限，因此对速比变化率进行合理限制是提高急加速等瞬态工况性能的关键.

现有的控制方法建立在车辆参数及路况信息已知的基础上，利用整个传动系统的受力平衡关系来计算允许的速比变化率，并以此作为分析和控制的依据，故称为“白箱控制法”.如文献[12－13]中给出的速比变化率限制值为：

式中Temax为发动机在当前转速下的最大转矩，r为车轮半径，i0为主减速比，f为滚动阻力系数，Cd为风阻系数，A为迎风面积.式中速比变化率的计算需要已知车辆及路况信息，仅适用于良好平路行驶时的急加速工况，一旦脱离公式中所规定的工况，比如路面存在坡度、滚动阻力系数改变、车辆载重发生变化等都会降低控制效果，该控制方法在实车工况下难以保证控制精度，没有普遍适用性.

要保证控制方法具有普遍适用性，就必须避免对车辆及路况信息的依赖，而应该以直接测量或计算得到的参数作为控制目标.列举可以直接获取的信号，容易发现，将CVT输入功率或者车速作为控制目标较为合适，解释如下.

1）目前基于功率需求的控制策略成为研究的主流[7]，也更符合驾驶员的预期[2－3]，以 CVT 输入功率作为控制目标能够和功率需求控制策略相兼容，程序设计比较容易.CVT输入端的功率为：

式中Te和ωe可实时计算或测量得到，发动机及飞轮惯量Ie已知，无需其他车辆及路况信息.

2）由于最终影响驾驶员主观感受的是车速变化，因此最直接的控制方法是以车速或加速度作为控制目标.

基于输入功率和车速的控制方法不依赖于车辆及路况信息，但又根据传动系统特性来选择目标参数和设计控制算法，因此称为“灰箱控制法”.

2 瞬态工况下的功率补偿控制

各种控制方式都可理解成是对发动机和飞轮转速变化所吸收或释放的功率进行不同程度的补偿.补偿控制应在保证舒适性的前提下优先调节速比，使车辆尽可能快地过渡到目标工况.本文重点讨论以CVT输入功率作为控制目标的控制方式.

2.1 基于有效功率的补偿控制

所谓基于有效功率的补偿控制，是指以设定的CVT输入功率作为控制目标，而不是以发动机功率作为控制目标，通过调节节气门开度和速比变化率实现该目标功率.通过分层次量化补偿功率，将控制方法划分为功率维持、零功率、增加后备功率和综合模式等4种控制模式，并给出了控制模型.

1）功率维持控制是以输入功率维持不变作为控制目标，即dPin／dt＝0.对于急加速过程，为防止目标量偏移，改为以输出功率不降低作为控制目标，即dPin／dt≥0，其实质是速比增大过程中发动机增加的输出功率正好能够补偿惯量Ie所吸收的功率.

在该控制模式下，若忽略变速过程中的车速变化和路况变化，其控制效果近似为加速度不降低.一种特殊工况是车辆处于上坡等重载工况，且处于减速运行状态，即加速度为负，维持功率不变可以保证减速度不再降低.

2）零功率控制是以输入功率接近为零作为控制目标，即Pin≈0.对于急加速过程，为防止控制偏差过大，改为以输出功率不小于零作为控制目标，即Pin≥0，其实质是速比增大过程中惯量Ie所吸收的功率完全由发动机功率提供，不出现反拖工况.该补偿模式的控制效果类似于空挡滑行或AMT换挡过程中的动力中断.

现有控制方法对需求功率快速降低的减速工况研究较少，但是同样需要进行适当考虑.与急加速过程类似，在加速踏板开度突然减小时，目标速比也随之减小，此时的附加力矩为驱动力矩，如果速比变化率过大，有可能出现车辆前冲的感觉.减速工况下的补偿控制与加速工况类似，可进行统一表示，公式（7）和（8）分别为功率维持和零功率两种控制模式的目标表达式：

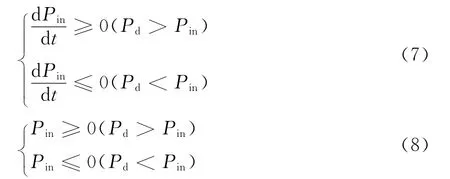
3）增加后备功率的补偿控制.功率维持和零功率两种控制模式是在需求功率变化之后给予补偿控制，以牺牲动力性来改善舒适性，属于被动响应控制.如果对加速性能要求较高，通过在稳态工况下适当提高速比来增加后备功率，则有利于提高车辆的加速性能.

通常情况下，在发动机最佳经济线附近的一定范围内，效率平台相对比较平缓，适当增大速比能够有效提高后备功率.例如，以式（9）所计算的功率Pcal代替Pd来确定目标速比，此时发动机目标转矩下降，以维持功率不变：

式中kp为放大系数，kp≥1，Cp为最小后备功率，则后备功率增加量为：

增加后备功率的极端情况是以发动机最大功率Pemax对应的发动机转速ωepmax作为目标转速确定速比，即

此时发动机具有在当前车速下的最大后备功率，具有最好的加速性能，但效率很低.在急加速时，仅通过调节节气门开度就可使车辆获得当前车速下可能的最大功率，快速响应车辆的加速需求，并且因为无需调节速比或者只需小范围调节速比，附加转矩的影响大大减小.

4）综合模式补偿控制 .驾驶员对车辆加速性能的评价具有主观性，将单一控制模式应用于所有工况不易达到满意效果，通过将上述不同层次的控制模式进行综合可进一步优化控制效果.典型的综合方式分为3种：①时间段综合，分时间段采用不同的控制模式；②控制量综合，采用加权法综合各种控制模式；③同时采用时间段综合与控制量综合.

综合方式的实施可依据实车试验中驾驶员的主观评价进行调整，灵活地设定不同的过渡曲线以优化瞬态工况特性.

2.2 直接以车速为目标的补偿控制

与基于有效功率的控制方法类似，以车速为目标的控制方法可划分为加速度维持和速度维持2种控制模式，式（12）和（13）分别为两种控制模式的目标表达式.该控制方法的基本思想比较直观，重点在于研究控制算法，本文不做论述.

2.3 补偿控制的实现

基于有效功率的补偿控制模型如图2（a）所示，相对于传统控制方法增加了功率补偿控制模块，图中功率控制以外的其他模型简化为虚线框表示.加速踏板开度θ对应需求功率Pd；需求功率Pd（或Pcal）和车速v确定目标速比itgt；根据公式（6）计算有效功率Pin；功率补偿控制模块判断当前工况确定目标节气门开度αcal和修正目标速比ical；节气门控制器和速比控制器驱动执行机构达到目标值.

补偿控制模型如图2（b）所示，主要是工况判断和逻辑控制.目标节气门和目标速比控制采用模块化的设计方法，用于不同工况和不同补偿控制模式的调用.补偿模式分为增加功率、维持功率和降低功率3种情况，首先调节节气门开度进行补偿，若节气门已达到极限值仍不能满足要求，再通过改变目标速比来调节速比变化率.图中所示为功率维持模式，将dPin／dt≥0改为Pin≥0即为零功率模式.

图2 基于有效功率的补偿控制模型Fig.2 Compensate control model base on effective power

3 仿真与试验

以JL472Q1发动机和C075无级变速器组成的传动系统为研究对象，对不同控制方法进行仿真和试验.由于加速过程是研究的重点，且减速过程与加速过程的控制方法类似，因此下面只给出加速过程的仿真和试验结果.

3.1 加速工况仿真

中速轻载工况转变为中速重载工况时，需求功率和速比变化范围大，有利于考验控制方法的效果.将仿真行驶工况设定为：①加速踏板开度0.1，车辆稳定行驶；②加速踏板开度阶跃为1，速比开始变化，车辆进入急加速过程.仿真结果如图3所示，4种控制策略因补偿程度不同而具有明显不同的控制效果，补偿控制方法能够实现设定的控制目标，而常规控制方法则出现反拖工况，造成转速快速下降，违背驾驶意图.

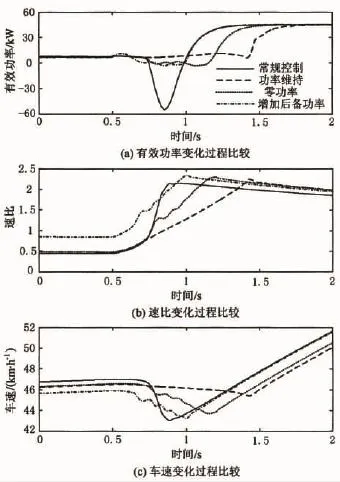
图3 加速工况仿真结果Fig.3 Simulation results of hard acceleration condition

图4 加速工况试验结果Fig.4 Experiment results of hard acceleration condition

图中显示，工况过渡过程分为两个阶段：第1阶段是速比调节阶段，发动机功率主要用于提高自身转速，由于系统的响应滞后及速比控制算法的因素，速比变化滞后于需求功率的变化；第2阶段是车辆加速阶段，此时实际速比与目标速比接近，发动机功率主要用于驱动车辆加速.

仿真结果与分析结论相同：功率维持模式下，车速基本维持稳定；零功率模式下，车速因行驶阻力的作用而缓慢下降，接近于空挡滑行；增加后备功率的控制模式能够在速比调节阶段保持功率为正，同时具有和常规控制模式接近的加速性能，但系统效率有所降低.

3.2 加速工况试验

根据现有CVT试验台条件，并考虑急加速过程可能造成的试验风险，在试验过程中减缓加速过程并降低发动机功率.试验工况设定为：①加速踏板开度0.05，车辆稳定行驶；②加速踏板开度在0.5s时间内线性上升至0.75，车辆进入加速过程.试验结果如图4所示，由于信号采集误差和干扰等因素，对试验数据采用移动平均法进行滤波处理，滤波区间为20ms.

试验结果表明，因为需求功率逐渐增加，车辆的加速过程平缓很多.速比控制算法依据仿真模型设计，在进行台架试验中并未做大的调整，由于模型误差，尤其是CVT液压系统模型的误差，影响了试验控制效果，但是工况过渡曲线的基本特征与仿真结果是一致的.从有效功率曲线看，常规控制方式出现了发动机反拖工况和车速快速降低阶段，而补偿控制方法均基本实现了设定的控制目标.由于加速过程比较平缓，零功率控制模式下的实际有效功率始终为正.3种控制模式完成速比调节进入加速阶段的先后次序与仿真结果也相同.

4 结 论

1）提出了瞬态工况下以有效功率和车速作为控制目标的通用补偿控制方法，克服了现有控制方法依赖于车辆及路况信息的缺陷.

2）通过分层次量化补偿功率，将控制方法划分为功率维持、零功率、增加后备功率和综合模式等4种控制模式，为灵活设定过渡曲线和优化瞬态工况性能提供了量化依据.

3）仿真和试验结果表明：功率补偿控制方法能够实现所要求的补偿效果，克服加速过程中的动力疲软，验证了控制方法的可行性和通用性.

[1] NILABH S，IMTIAZ H.A review on belt and chain continuously variable transmissions（CVT）：dynamics and control[J].Mechanism and Machine Theory，2009，44：19－41.

[2] DIPAK P，JEFF E，MIKE O.CVT drive research study[C]／／SAE International Transmission and Drivelines Symposium－4WD／AWD：SAE World Congress.Detroit，Michigan，USA，2005：2005－01－1459.

[3] DAVID F P，DONG Y D W，ROBERT W P，etal.Dead pedal and the perception of performance of a continuously variable transmission[C]／／SAE International Transmission and Drivelines Symposium－4WD／AWD：2005SAE World Congress.Detroit，Michigan，USA，2005：2005－01－1596.

[4] ALEX F A S，SHEN S W，FRANS E V.Control of a flywheel continuously variable transmission[J].ASME，Journal of Dynamic Systems Measurement and Control，2003，125：455－461.

[5] 刘金刚，周云山，邹乃威，等.DMC－PID串级控制在CVT速比控制系统中的应用[J].湖南大学学报：自然科学版，2007，34（10）：44－48.LIU Jin－gang，ZHOU Yun－shan，ZOU Nai－wei，etal.Application of DMC－PID cascade control in CVT speed ratio control system[J].Journal of Hunan University：Natural Sciences，2007，34（10）：44－48.（In Chinese）

[6] 邹乃威，王庆年，刘金刚，等.金属带式CVT速比的改进PID控制[J].湖南大学学报：自然科学版，2008，35（8）：29－33.ZOU Nai－wei，WANG Qin－nian，LIU Jin－gang，etal.An improved PID algorithm for the ratio control of metal belt CVT[J].Journal of Hunan University：Natural Sciences，2008，35（8）：29－33.（In Chinese）

[7] PFIFFNER R，GUZZELA L，ONDER C H.Fuel－optimal control of CVT power trains[J].Control Engineering Practice，2003，11：329－336.

[8] 张树培，张友坤，王庆年，等.非稳态工况下无级变速器传动比控制优化[J].吉林大学学报：工学版，2010，40（4）：895－900.ZHANG Shu－pei，ZHANG You－kun，WANG Qing－nian，et al.CVT ratio control strategy optimization under non－steady working condition[J].Journal of Jilin University：Engineering and Technology Edition，2010，40（4）：895－900.（In Chinese）

[9] LEE H，KIM H.Improvement in fuel economy for a parallel hybrid electric vehicle by continuously variable transmission ratio control[J].IMechE，J Automobile Engineering，2005，219（Part D）：43－51.

[10] KIM T，KIM H.Performance of integrated engine－CVT control considering powertrain loss and CVT response lag[J].IMechE，J Automobile Engineering，2002，216（Part D）：545－553.

[11] KIM T，KIM H.Low level control of metal belt CVT considering shift dynamics and ratio valve on－off characteristics[J].KSME，2000，14（6）：645－654.

[12] 邓涛，孙冬野，秦大同，等.无级变速传动系统综合控制仿真与试验[J].汽车工程，2010，32（1）：49－55.DENG Tao，SUN Dong－ye，QIN Da－tong，etal.Simulation and test of integrated control for continuously variable transmission system[J].Automotive Engineering，2010，32（1）：49－55.（In Chinese）

[13] 罗勇.金属带式无级变速传动系统匹配控制研究[D].重庆：重庆大学机械工程学院，2010.LUO Yong.Study on matching and controlling of power－train system equipped with metal belt continuously variable transmission[D].Chongqing：College of Mechanical Engineering，Chongqing University，2010.（In Chinese）