渡槽模型实测模态合成的研究＊

李正农，卢 剑，朱旭鹏，李继孟，张盼盼

（1.湖南大学 建筑安全与节能教育部重点试验室，湖南 长沙 410082；2.云南省设计院，云南 昆明 650032）

模态综合技术又称为子结构法[1－3]，其基本思想是通过将结构划分为若干相对较小的子结构，先分析子结构的动态特性，然后将各子结构的低阶模态通过界面协调条件合成为总体结构的模态[4－5]，从而减少计算量.

在实际的工程中，很多结构都具有对称性，其振动形式也具有对称的性质，在进行模态实测及分析的时候，可以利用结构的对称性来减少工作量以及工作成本[6].

本文利用结构对称性推导得出了一个简单易行的模态组合方法，即模态调整系数法.

1 模态分析的数学模型

将结构离散化为若干自由度后，在物理坐标系统中，N个自由度系统的方程为：

式（2）中α和β为比例常数，[C]称为比例阻尼，[M]为质量矩阵，[K]为刚度矩阵.进行相同的变换，得：

式中 ｛φr｝为由 [M]｛｝＋[K]｛x｝＝0所确定的第r阶 模态振型.将式（3）代入式（1）得：

式（4）左乘以 ｛φs｝T，并考虑到

cs可称为模态阻尼系数.于是式（4）变为：

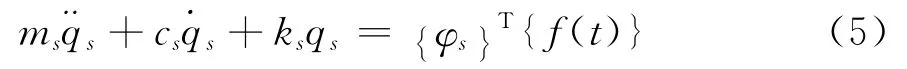
令f（t）＝ ｛F｝ejωt，则qs＝Qsejωt，代入式（5）

可以看出Qs相当于一个质量、刚度和阻尼分别为ms，ks，cs的单自由度系统在模态力Ps＝｛φs｝T｛F｝作用下的响应.

根据式（3），不考虑起始条件，可得位移响应为：

式（7）即为具有比例阻尼的系统进行响应计算的模态模型.

2 组合系统的频响特性的分析

图1所示，两部件系统在F1作用下在1点产生的位移为X1，连接点位2的位移为X2.

取分离体后，连接处的作用分别以力FⅠ2及FⅡ2来代替.对于部件Ⅰ，可得：

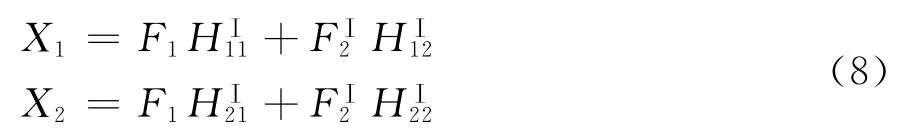
对于部件Ⅱ，可得：

在连接点，若以位移的方向为参考方向，则有：

于是由式（11）～（13）可得：

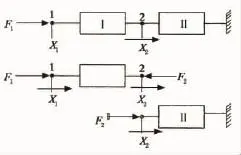
图1 两部件系统Fig.1 Two components system

式（11）的方程组共有3个方程，求解3个未知数，因此有唯一解.

3 两部件系统振型组合推导

模态分析的一种方法是通过找出激励点与各个测点之间的“频响函数”（也叫传函数），建立频响函数矩阵来进行分析.传函数定义为：

其中H为传函数，X为响应，F为激励力.式（12）即定义为i，j之间的传函数.其物理意义为：在j点作用单位力时，在i点所引起的响应.

在模态分析中假定系统是线性的.对于一个N自由度的线性系统，其位移响应可以看成各阶模态响应的线性叠加，那么其传函数同样是展成N个单自由度系统的传函数线性叠加，即：

其中kr，mr，cr，φr分别为第r阶模态刚度、模态质量、模态阻尼和模态振型.从式（13）抽取任意一行和任一列为：

从式（14）和式（15）可见，位移传函数矩阵[H]是对称的，它的任一行或任一列均包含所有模态参数，而该行的第r阶模态的传函数值之比值，即为第r阶模态振型.这一结论告诉我们，如果在结构上的某一固定点第i点拾振，而轮流地激励所有的点，即可求得传函数矩阵的一行；如果在某一固定点第j点激振、而在其他各点拾振，即可求得传函数矩阵的一列.两种方法均可用来获取传函数[7].

下面以传函数的任一列为例，[H]中的任一列包含全部模态参数，而该列的r阶模态的传函数之比值，即为r阶模态振型.令代入式（15）整理得：

本文以一个5自由度系统为例（如图2所示），推导两部件系统的振型组合关系.5自由度系统分为两个部件进行实验.第一部分为1，2，3三点所组成的部件Ⅰ，第二部分为由3，4，5三点所组成的部件Ⅱ，其中3点为两个部件所共有的点.假设部件Ⅰ以1点为参考点，部件Ⅱ以3点为参考点，整个系统的传函数矩阵为：

其中每行和每列都包含有系统的全部模态信息，而且矩阵是一个对称矩阵，所以部件Ⅰ实验得到的是部件Ⅱ所得到的传函数为如果想要得到系统的整体模态振型的话，就要得到传函数矩阵的一行或者一列.根据式（12）的含义可知以上两个部件所得到的传函数是有关系的：

由式（18）～（20）可解得：

同理

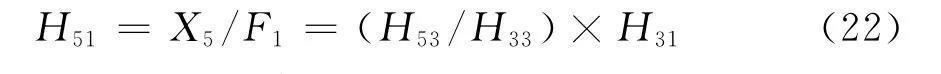
由此可得到传函数矩阵的一行，这样也就得到了整个系统要分析模态的全部信息.

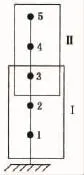
图2 五自由度系统Fig.2 Five DOF system

对两个部件分别进行模态测试后，得到部件Ⅰ的振型为 [φ1Ⅰφ2Ⅰφ3Ⅰ]T，部件Ⅱ两点的振型为[φ3Ⅱφ4Ⅱφ5Ⅱ]T.由于选择的参考点不一样.由式（16），（21），（22）得：

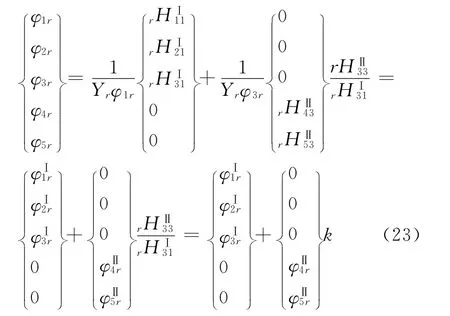
式中k＝rHⅡ33／rHⅠ31，φ为振型系数，r为第r阶模态.式（23）即为两部件系统振型组合的推导公式，其意义可以从两方面来解释.第一，以其中一个部件的振型为基础，另外一个部件的振型系数乘以系数k以后相组合就能得到系统的整体振型.第二，由于部件Ⅰ和部件Ⅱ有共同测点3，乘以系数k后能使两个部件在3点的振型系数相同，满足变形的协调条件，所以在分别知道两个部件的振型之后，利用变形协调条件把某个部件乘以系数k后能得到整体振型.

4 实 例

4.1 模态实测概况

以一个桩－槽墩系统的模态实测及模态合成为例说明本文的方法.具体的模型见图3，其下部采用4根钢管桩，钢管内径147mm，钢管桩的编号见图6.4根桩采用重锤打入土中，在打入图中前在①②两根桩中分别贴有24个应变片，③④桩中分别装有13个土压力计.桩中线路错综复杂，布置加速度传感器的难度很大，而且可能对线路造成不可逆转的损坏.所以为了完成实验，并对应变片的损伤降到最低，本次实测只对一根桩进行了模态测试，然后根据前面推导的理论把他还原成桩－槽墩整体模型，得到其整体自振特性.

图3 实验模型Fig.3 Test model

4.2 模型建立及模态分析

具体进行了两项实测，即上部结构模态实测及桩的模态实测.系统总体使用笛卡尔全局坐标系.考虑结构的对称性及桩模态存在轴对称或点对称，仅对一根桩进行了测试，以减小实测的难度和工作量.其测点布置分别见图4、图5.组合以后的桩－槽墩整体模型见图6.

图4 桩测点布置Fig.4 The sensor arrangement of the pile

本文采用峰值法（PP）估计频率[8]，并采取平均技术[9]处理试验数据.模态测试采用武汉优泰电子技术有限公司生产的UT3308动态测试系统完成，模态参数的分析及识别由优泰结构与机械模态分析软件完成.模态拟合方法采用频域法中的实模态多自由度整体拟合方法.

图5 上部结构测点布置Fig.5 The sensor arrangement of the upper structure

图6 桩－槽墩模型Fig.6 The pile－pier modal

4.3 实测结果

由于模态实测是分桩和上部结构两部分进行的，而且仅对其中一根桩进行了实验，故在进行整体模态分析时，分别建立单桩模型，槽墩模型以及桩－槽墩整体模型，见图4、图5及图6.单桩模型以及槽墩模型模态图见图7和图8.而对于桩－槽墩模型，先把相应的传函数赋予各个测点，由于对称性4根桩的传函数都是一样的，全为桩①的复制.对其识别出频率以及相应的振型之后，由于模态实验时桩与槽墩所选择的参考点不同，要把这两者模态统一起来，可以根据本文推导出来的理论，把单根桩的模态振型系数统一乘以系数k后振型组合，得到整体振型.具体结果见图9.

桩的振型调整系数k见表1，单桩槽墩的实测频率、组合后的整体结构模态的频率及有限元模态计算结果见表2.从表2可以看出在系统的自振频率上试验与计算结果基本一致.

图7 桩模态图Fig.7 Mode of pile

图8 槽墩模态图Fig.8 Mode of pier

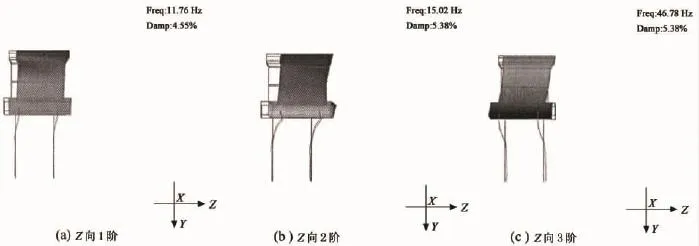
图9 桩－槽墩模态图Fig.9 Mode of pile－pier

表1 振型调整系数kTab.1 Modal adjustment coefficientk

表2 桩与槽墩的自振频率及组合后的频率Tab.2 Natural frequency of the pile and pier and the combination structure Hz

5 结 论

通过以上的分析，可得到以下结论：

1）推导出了两部件系统振型组合的简化理论，并将此理论应用于具体的实测模态组合.

2）利用结构的对称性，简化模态测试的过程，减少了实测工作量及成本.

3）通过实测获得了桩和槽墩各自的自振频率和振型，进而组合获得了桩－槽墩系统的总体模态，并进行了有限元计算理论，两者基本吻合.

[1] BOUHADDI N，LOMBARD J P.Improved free－interface substructures representation method[J].Computers and Structures，2000，77：269－283.

[2] 向树红，邱吉宝，王大钧.模态分析与动态子结构方法新进展[J].力学进展，2004，34（3）：289－303.XIANG Shu－hong，QIU Ji－bao，WANG Da－jun.The resent progresses on modal analysis and dynamic sub－structure methods[J].Advances in Mechanics，2004，34（3）：289－303.（In Chinese）

[3] WANG Xiao－yun，JAMES K Mills.Dynamic modeling of a flexible－link planar parallel platform using a sub－structuring approach[J].Mechanism and Machine Theory，2006，41：671－687.

[4] KIM Dae－kwan，LED Min－su，HAN Jae－hung.Substructure synthesis method for a nonlinear structure with a sliding mode condition[J].Journal of Sound and Vibration，2009，321：704－720.

[5] SHANMUGAM A，PADMANABHAN Chandramouli.A fixed－free interface component mode synthesis method for rotordynamic analysis[J].Journal of Sound and Vibration，2006，297：664－679.

[6] 郭云霞，安晓卫，杨红民.结构对称性在活塞有限元模态分析中的应用[J].沈阳理工大学学报，2006，25（2）：56－58.GUO Yun－xia，AN Xiao－wei，YANG Hong－min.Application of symmetry of the structure in finite element modal analysis of the piston[J].Journal of Shenyang University of Technology，2006，25（2）：56－58.（In Chinese）

[7] 李德葆，陆秋海.实验模态分析及应用[M].北京：科学出版社，2001：58－67.LI De－bao，LU Qiu－hai.Experimental modal analysis and application[M].Beijing：Science Press，2001：58－67.（In Chinese）

[8] 戴恩彬，任伟新.湛江海湾大桥环境振动实验与模态分析[J].中国水运，2009，9（11）：167－169.DAI En－bin，REN Wei－xin.Ambient vibration test and modal analysis of Zhanjiang Gulf Bridge[J].China Water Transport，2009，9（11）：167－169.（In Chinese）

[9] 张爱林，王冬梅，刘学春，等.2008奥运会羽毛球馆弦支穹顶结构模型动力特性试验及理论分析[J].建筑结构学报，2007，28（6）：68－75.ZHANG Ai－lin，WANG Dong－mei，LIU Xue－chun，etal.Dynamic performance experiment and theoretical analysis on the suspend－dome structure model of the badminton gymnasium for 2008Olympic Games[J].Journal of Building Structures，2007，28（6）：68－75.（In Chinese）