电力扰动信号的小波形态学去噪方法

陈晓娟，李松寒，隋吉生，王 丽

(1.东北电力大学信息工程学院，吉林 吉林132012;2.吉林省电力有限公司，吉林 长春130021)

0 前言

随着人们生活水平的不断提高，对电能质量也提出了越来越高的要求。由于大容量电力设备和用电整流设备的投入以及其他非线性负荷的影响，不可避免地会发生各种电能质量扰动，其主要表现形式为电压凹陷、降落和瞬时扰动等。任何扰动都会对电能质量造成破坏。因此，如何找出扰动现象的规律，并及时地采取相应措施以避免扰动及其带来的损失日益成为提高电能质量中的重要课题。为了更好地监测电力系统的运行状态，大量的电力监测装置广泛应用在电力系统中。但采集到的信号通常含有噪声，为了精确地反映被采集信号量的特征，必须对其进行去噪处理，通常采用小波变换的方法［1］。但有些扰动信号的小波变换系数值可能与噪声的小波变换系数值相近，且低于阈值被当作噪声去掉，导致信号部分失真。而基于形态学的方法［2］，由于其计算速度快、实时性强的优点，应用于信号消噪也取得了较好的效果，但并未应用在电力扰动信号的处理。本文就如何取得更好的去噪效果进行了讨论，并对以上几种方法进行了分析和仿真，并创新地提出了小波形态学相结合的去噪方法，该算法的实质是采用形态学的方法消除大部分的噪声，然后再利用特殊处理后的阈值经过小波变换对其做平滑处理，从而使信号的失真度大大降低，而且能够有效消除噪声。

1 小波去噪和形态学原理

1.1 小波去噪原理

在实际电力系统发生扰动时，通过监测装置采集到的扰动信号都是含噪的非平稳信号，信号在任一时刻附近表现出的频率特性都很重要，仅从时域或频域上来分析是不够的。由于传统去噪方法的种种限制，小波理论在信号去噪领域逐渐受到了许多学者的重视。目前，小波消噪的方法主要分为小波分解与重构法、非线性小波变换阈值法、平移不变量法和小波变换模极大值法。其中，非线性小波变换阈值法应用范围比较广泛，通常适用于处理的信号中含有随机白噪声的情况，尽可能多的保留原始信号的重要信息，也能对原始信号进行很好的估计，并且计算速度也比较快。因此，本文以此方法为例来说明小波去噪的基本原理。其具体的处理步骤如下［1］:

(Ⅰ)选择合适的小波基函数，运用小波变换的方法对含噪的信号进行N层分解(小波分解的层数需根据噪声的相关类型进行确定)。

(Ⅱ)小波分解高频系数的阈值量化。根据相关的阈值选取规则，对以上进行小波分解尺度下的高频系数进行阈值量化处理。阈值量化处理大体分为软阈值量化处理方法和硬阈值量化处理方法两种。

(Ⅲ)对经过上述处理过后的底层低频系数和各层的高频系数进行一维小波重构。

在以上的这3个步骤中，最关键的是小波基的选取以及阈值的选取和量化，这在某种程度上关系到信号去噪质量的好坏。

1.2 数学形态学的基本原理

数学形态学是一种非常有效的非线性滤波技术。运用形态学在进行信号处理时，需不断移动结构元素以便提取信号中的有用信息。与传统滤波技术相比，该方法易于实现且计算时间少。目前，数学形态学主要应用在电力系统中的继电保护［3］和信号去噪［4］等方面。由于电力系统信号分析和处理中所涉及到的信号通常是一维信号，本文就一维离散情况下的多值形态变换(包括膨胀运算、腐蚀运算以及此两种运算级联组合所构成的运算)进行分析。

设输入信号序列和结构元素分别由f(n)和g(n)代表，则f(n)关于g(n)的膨胀和腐蚀具体计算公式分别如下:

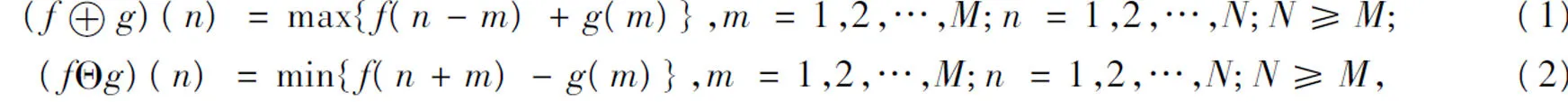
式中，⊕、Θ分别为膨胀、腐蚀的运算符号。

形态开运算和闭运算是基于膨胀和腐蚀运算的基础上进行展开的，其具体计算公式分别如下:

式中，°、●分别为形态开运算和形态闭运算的运算符号。

在大多数形态滤波器的构造中，开运算通常被用于正脉冲噪声的去除，而闭运算则是常被用于负脉冲噪声消除。考虑到开运算和闭运算去除噪声的类型，Maragos则采用基于开闭运算的级联组合方式，即形态开－闭(OC)和闭－开(CO)滤波器。其定义式如下:

由于开运算的反扩展性和闭运算的扩展性会造成经过开－闭滤波器处理后的信号幅度偏小，而经过闭－开滤波器处理后的信号幅度偏大，所以单独使用它们并不能获得良好的滤波效果。为了获得更好的去噪效果，通常采用开－闭滤波器和闭－开滤波器的平均组合方式，其定义式如下:

经过形态滤波器处理效果的好坏不仅取决于上述形态运算的方式，而且还取决于结构元素的形状和长度［4］。经过大量的现场实验证明:平滑的半圆形结构元素通常被用来抑制电力信号中常见的白噪声;三角形的结构元素则常被用来进行含有脉冲噪声的信号处理［3］。另外，所选取的结构元素长度过大或者过小都不能达到很好去噪效果，同时也会破坏原信号的结构。文献［5］指出采用长度为信号周期长度的1/50～1/20的结构元素是比较适合的。

2 小波形态学融合算法

小波变换在非平稳信号的处理上效果显著，形态学则在时域的处理上具有很好的效果且较为简单。本文将此两种算法融合进行消噪，算法的具体步骤如下:

(Ⅰ)选择合适的小波基函数和适当的尺度，将含有噪声的扰动信号进行N层小波分解(本文是进行3层小波分解)，提取各层的小波系数。

(Ⅱ)根据相应结构元素选择规则［6］对各尺度下的小波系数进行选取结构元素，然后采用交替混合型形态滤波器进行滤波，进而得到新的小波系数。

(Ⅲ)根据相关阈值求解方法［5，7］进行阈值的求解，再将此阈值与系数k(0＜k＜1)进行相乘。然后，再利用软阈值方法对新的每一层的小波系数进行阈值量化处理。其中系数k的值是采用自适应方法求得，其具体计算方法如下:

3 仿真及结果分析

如图1所示的扰动信号为例，然后对其叠加白噪声和随机背景噪声。从图1中可以看出:模拟出的扰动信号已经被噪声完全给淹没了，不能确定其中是否含有扰动信号，更不能直观地看出哪些是有用的信息。

3.1 形态学的信号去噪

本文运用形态学的信号去噪处理，所选用的结构元素为扁平结构元素、长度为13交替滤波器(这样可以解决信号处理后的单向偏移问题)。从其处理结果(见图2a)所示，运用数学形态学处理过后的信号存在很多毛刺，而且丢失了很重要的原信号信息。

3.2 小波方法的信号去噪

考虑到中国配电网线路上的实际噪声情况，本文应用非线性小波变换阈值法［1］对扰动信号进行处理。根据电力系统暂态信号分析中小波基的选择相关原则［8］，选取的小波基是与所模拟扰动信号波形相似的db5小波对含噪的扰动信号进行4层分解。去噪阈值选取按照‘heursure’和‘minimaxi’两种阈值选择规则进行设定，其仿真结果如图2b、图2c所示。此两种方法在去除噪声的同时还去除掉了原信号的一些特征，不利于对扰动信号进行后期的处理。

图1 原始扰动信号及含噪扰动信号

3.3 小波形态学融合的信号去噪

本文选择与扰动信号相似的小波基函数db5并对含噪的信号进行3层分解，然后对各尺度下的小波系数选取长度为10、13、11的扁平结构元素，采用交替混合型形态学滤波器进行滤波，得到新的小波系数。利用软阈值对新的每一层的小波系数进行阈值处理，然后运用阈值处理过后的小波系数来重构消噪后的信号，其结果如图2d所示。从图2中可以看出:该方法不仅有效地去除了噪声，而且还保留信号在突变位置的相关信息，失真度很小。

以上只是通过主观的方法比较，可看出基于小波－形态学融合的去噪方法明显好于其他的去噪方法。但是为了更好地从原理上说明，采用客观的误差评价方法，其计算公式如下:

其中，Y(i)与X(i)为原始信号和消噪后的信号。

利用公式(9)对这3种方法的误差进行估计，计算结果如表1所示。

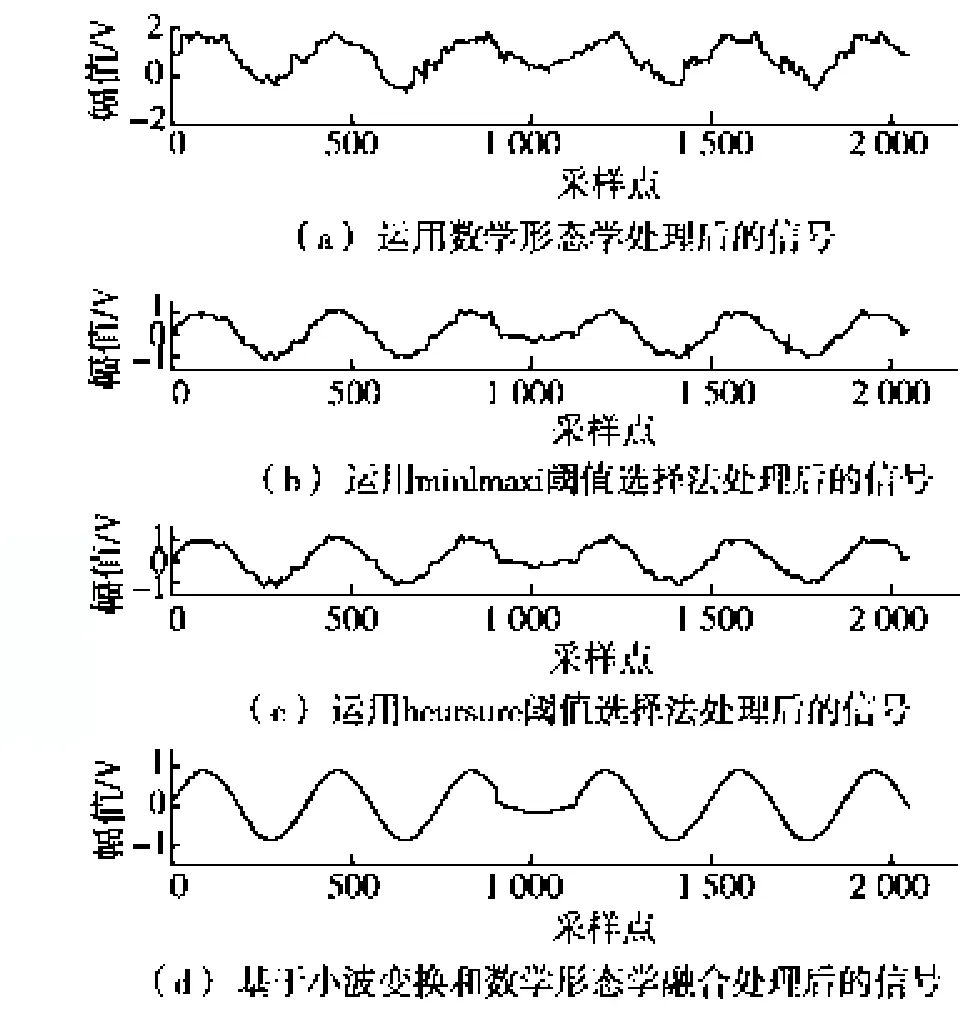
图2 运用各种方法消噪后信号波形

表1 各种方法的评价指标

从表1可以看出:基于小波－形态学融合的去噪方法优于其他两种方法。

4 结论

在电力系统暂态信号分析应用中，必须根据所要求的精度、速度等相关因素选取合适的信号处理方法以达到满意的处理效果。单独使用小波或形态学进行去噪，都会造成原信号的部分失真。本文将此两种方法进行融合以便达到很好的去噪效果。仿真结果证明:融合的去噪方法能很好地保留原信号的重要信息，且信号的失真度非常小，有很强的实用性。

［1］何慧，顾洁.电能质量信号的小波阈值去噪［J］.电力系统及其自动化学报，2010，22(2):103－108.

［2］尹文琴，刘前进.数学形态学在电力系统中的应用综述［J］.继电器，2007，35(19):76－83.

［3］李庚银，罗艳，周明，等.基于数学形态学和网格分形的电能质量扰动检测及定位［J］.中国电机工程学报，2006，26(3):25－30.

［4］张文斌，杨辰龙，周晓军.形态滤波方法在振动信号降噪中的应用［J］.浙江大学学报，2009，43(11):2096－2099.

［5］欧阳森，宋政湘，陈德桂，等.小波软阈值去噪技术在电能质量检测中的应用［J］.电力系统自动化，2002，26(19):56－60.

［6］赵昭，刘利林，张承学，等.形态学滤波器结构元素选取原则研究与分析［J］.电力系统保护与控制，2009，37(14):21－25.

［7］张磊，潘泉，张洪才，等.小波域滤波阈值参数 c的选取［J］.电子学报，2001，29(3):400－402.

［8］何正友，钱清泉.电力系统暂态信号分析中小波基的选择原则［J］.电力系统自动化设备，2003，25(10):45－48.