群桩基础中土工参数相关范围的分析
2011-07-13吴会阁王葛建龙
吴会阁王 丽,葛建龙
(1.石家庄经济学院 工程学院,河北 石家庄 050031;2.河北省水资源可持续利用与开发重点实验室,河北 石家庄050031;3.北京中铁建筑工程设计院 天津分院,天津300011;4.天津振津工程集团有限公司,天津300222)
0 前言
在越来越多的高层建筑和高重构筑物设施中,群桩基础以其承载力高、沉降小、生命力强等特点得到了广泛的应用。岩土工程参数的正确选取是群桩基础可靠性的重要保证,在各参数中土的物理性质和力学性质的空间变异性最大,描述这种空间变异性较好的方法是文献[1]提出的土工剖面的随机场理论,而反映土工参数空间变异特性的重要指标是土层的相关范围。近年来,国内外一些学者对土工参数的相关范围进行了一系列研究,文献[2]用一维平稳高斯随机场理论,研究了用回归模拟方法计算土工参数的相关范围;文献[3]用改进的空间递推平均法讨论了土工参数相关范围的确定;文献[4]用非线性曲线拟合法计算了土性的相关范围;文献[5]用相关函数法讨论了相关范围确定中相关函数的选取及拟合区间;文献[6]对目前确定土工参数相关范围的几种方法进行了评述,指出空间递推平均法虽计算方便,但平稳点难以确定,其计算结果受人为因素影响较大,曲线拟合法算出的相关距离值偏小。
在对群桩基础的可靠度分析时,本文拟采用相关函数法和变异函数法计算土工参数的相关范围。
1 土工参数的空间变异性
在天然土层中,土性指标在各点是确定的,根本不存在随机性的问题,“唯一”不确定的问题是无法知道土工参数在土层中每一点的取值[7]。
土工参数的空间变异由以下3部分组成:
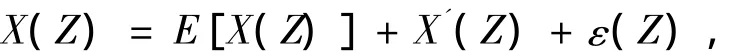
其中,E[X(Z)]为土工参数的趋势分量,是非随机的变量,可由最小二乘法回归;X'(Z)为零均值,方差为σ2的正态分布随机变量,{X'(Z)}为一平稳随机场,代表土性固有变异性;ε(Z)为测量误差。
对于平稳的随机场,其统计特征不随位置的不同而不同,其均值、方差以及自相关函数都可以通过样本相应的平均(随机过程的时间平均)得到。对于有连续变化的X'(Z)而言,由Shannon抽样定理,这时要求采样能再现原来连续曲线中含有的全部信息,从这一角度出发,取样间距越小、采样点越多越好;但取样间距太小,会增加点均值的统计误差、低估点的变异性。当取样间距小于相关范围时,由于土性自相关性的影响,用传统的独立、同分布序列统计方法计算“点”均值、“点”方差以及自协方差函数的无偏估计时,要加以修正。
2 两种算法的基本原理
2.1 相关函数法
2.1.1 相关函数理论[8-10]
对于一均质土层某一点t的土性记作x(t),则x(t)的概率特性可表示为:
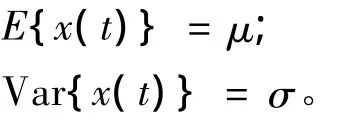
那么,土层中任意两点t,t+h之间的相关函数可用下式表示:
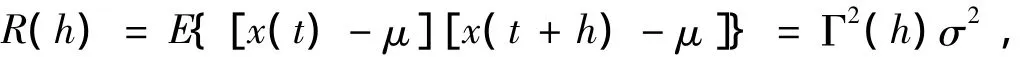
式中Γ2(h)为方差折减系数。
常用的理论相关函数有三角型、指数型、指数余弦型等,其对应的函数形式和相关范围(或变程)计算公式见表1。

表1 理论相关函数模型
2.1.2 相关范围的确定
用相关函数确定相关范围,就是用一定类型的理论相关函数模型去拟合实测相关函数曲线,求出相应参数,代入对应的相关范围计算公式求得结果。
相关函数法求解相关范围的步骤:
(1)原始数据的处理:将试验测得的原始数据X0i标准化后作为样本值Xi,即:
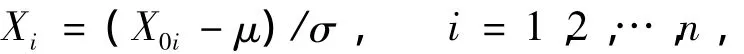
式中,μ,σ分别为原始数据的均值和标准差。处理后,样本均值为0,方差为1。
(2)取间距τ1=△Z,△Z为取样间距,计算相关函数值:
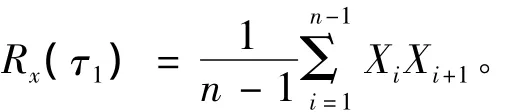
(3)分别取间距 τ2=2τ1,τ3=3τ1,…,τm=mτ1,…(m < n),分别计算出此时的相关函数值:
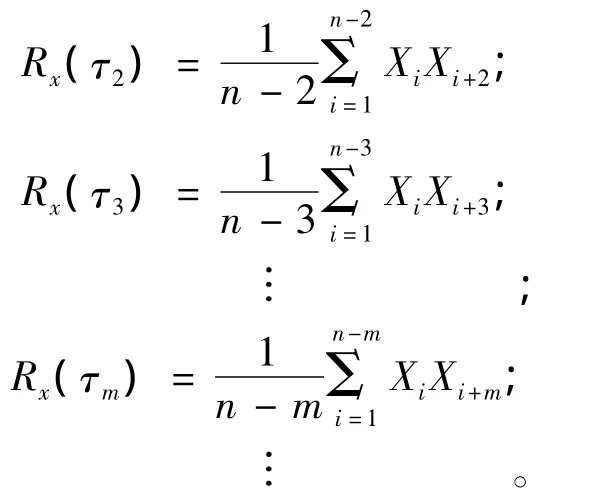
(4)此时,所得到的相关函数为实测的相关函数,可做出实测相关函数曲线,根据实测相关函数曲线选择合适的理论相关函数模型,对实测曲线进行拟合,把拟合出的相应参数代入计算公式即可。
2.2 变异函数法
2.2.1 变异函数理论
土的空隙度、相对密度、塑性指标、渗透系数、压缩模量、抗剪(压)强度以及某一特定持力土层的厚度都可看作是区域化变量。区域化变量一般可反映岩土参数的尺寸效应,不同程度的连续性和不同种类的异向性及空间变化的可迁性等特征。
对于一个代表岩土参数的区域化变量Z(x),变异函数可定义为向量h相隔的Z(x)、Z(x+h)两个区域化变量间增量平方的数学期望的一半,或两区域化变量增量的方差的一半(也称半变异函数),本文仍称之为变异函数:
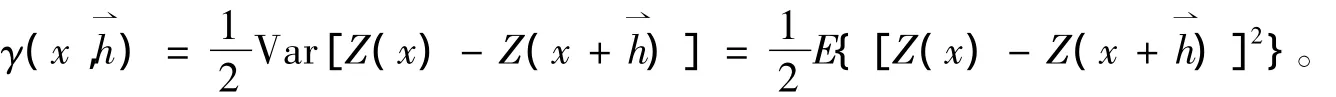
由上式可知:变异函数是点x和向量h两者的函数。由于在任意点上不可能获得一系列样本值,因此要求Z(x)满足本征假设条件,即可认为[Z(x)-Z(x+h)]只依赖于h,而不依赖于x,则可用实际观测值计算变异函数的估计量,即:
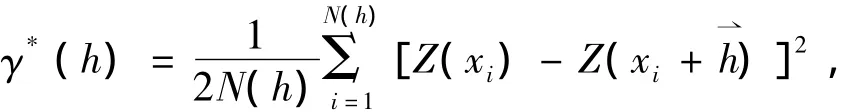
式中,N(h)是以向量h相隔的试验数据对Z(xi)和Z(xi+h)的数目。
常用的理论变异函数模型有球状模型、指数模型、高斯(Gauss)模型等,其中最常用的是球状模型。各种模型的函数形式及其对应的相关范围(或变程)值见表2和图1。

表2 理论半变异函数类型
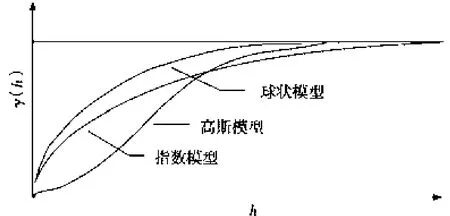
图1 理论变异函数模型
2.2.2 相关范围的确定
与相关函数法相似,变异函数法是用理论变异函数去拟合实测变异函数曲线,从而得出相应的参数,代入公式求得相关范围的值。
变异函数法求解相关范围的步骤:
(1)试验测得的原始数据作为样本值{X(t)},这时,样本均值为 μ,方差为 σ2。
(2)△Z为取样间距,取间距τ1=△Z,计算这时的变异函数值:
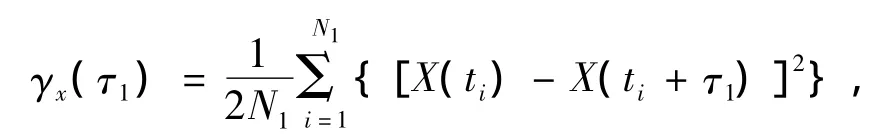
其中N1表示相距τ1的样本点对数。
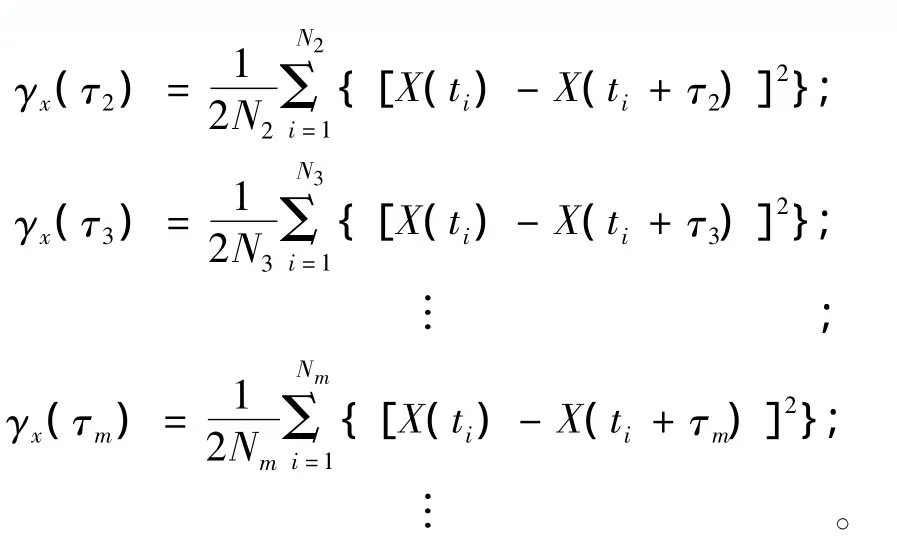
(4)此时,所得到的变异函数为实测变异函数,可做出实测变异函数曲线,根据实测变异函数曲线形式选择合适的理论变异函数模型对实测曲线进行拟合,求出参数后,便得到相关范围(或变程)值。
3 工程计算实例
图2为实测的天津地区某临近场地的静力触探曲线,fs为双桥探头测得的侧摩阻,kPa;qc为作用于探头上的阻力,MPa;h为相关范围,m。

图2 试桩静力触探曲线
基于指数模型,对各孔土层的相关范围分别采用相关函数法和变异函数法进行了计算。以J-5孔为例,具体计算结果如表3所示,考虑到计算结果的用途,本文只计算到桩端持力层,且计算结果为各土层侧阻的相关范围,对于端阻的相关范围,只考虑了桩端持力层。由表3可见:两种方法计算出的绝大多数土层的相关范围很接近,说明在对群桩基础的可靠性分析时,利用相关函数法和变异函数法均具有一定的可靠性,计算结果精度较高;少数结果有一定差距,为了降低计算结果的误差,推荐采用两种算法的平均结果。其余各孔的计算结果如表4所示,该结果为两种计算方法的平均值。
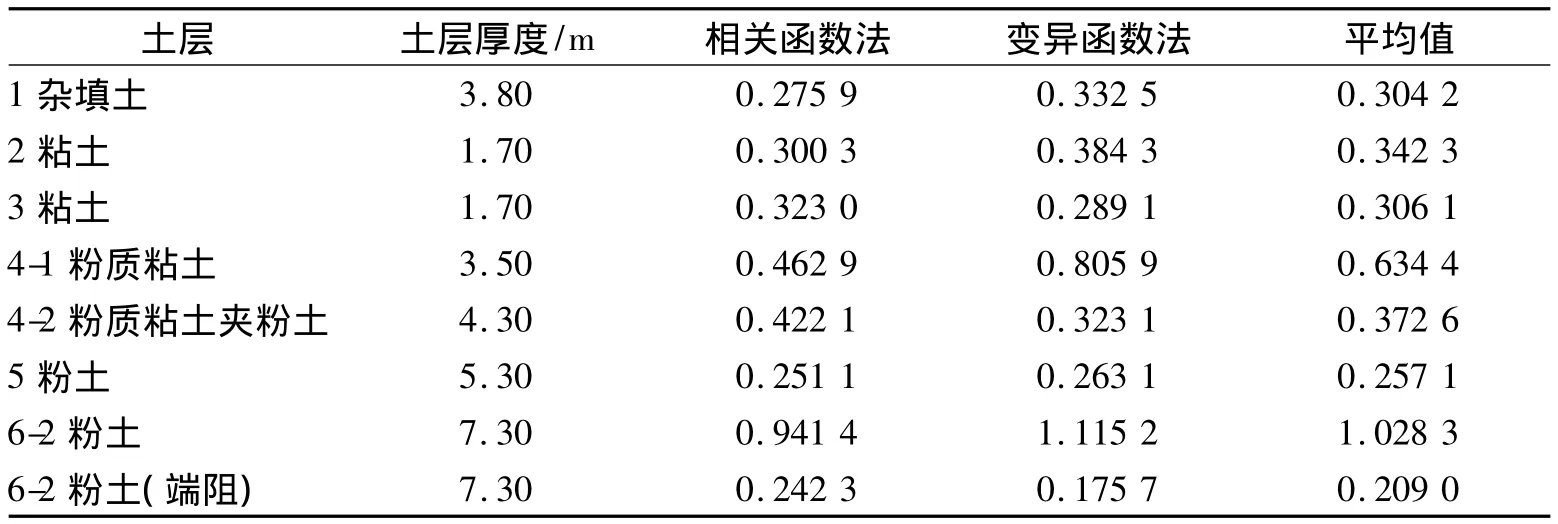
表3 J-5孔土层的相关范围
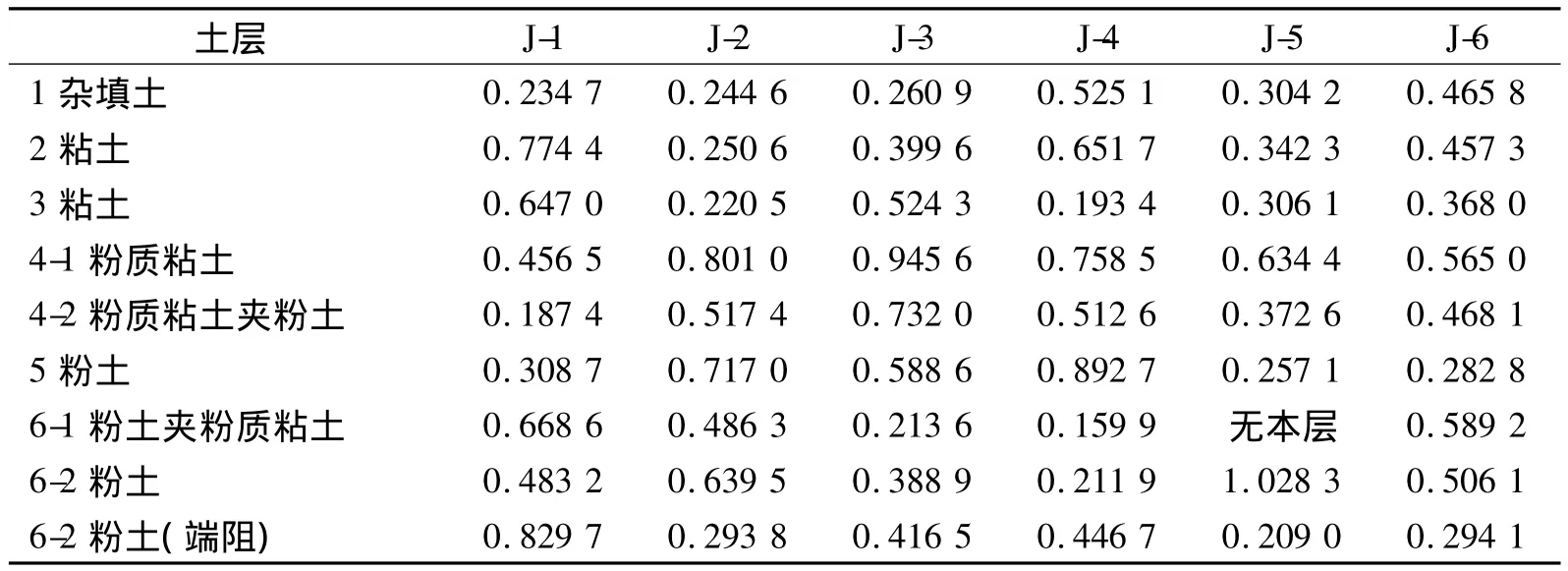
表4 各孔土层的相关范围
4 结论
(1)在钻孔灌注群桩基础的可靠度分析中,随机场理论是考虑土工参数空间变异性的重要方法。
(2)采用相关函数法和变异函数法对群桩基础中的相关范围进行研究,通过比较发现两种算法都具有较高可靠性。
(3)采用相关函数法和变异函数法计算结果的平均值,作为各土层的相关范围,可进一步减小如人为因素等原因引起的误差。
[1]Vanmarcke E H.Probabilistic Modeling of Soil Profiles[J].Journal of the Geotechnical Engineering Division,ASCE,1977,103(11):1227-1246.
[2]傅旭东.土工参数相关范围及相关距离的计算方法[J].西南交通大学学报,1996,31(5):510-515.
[3]张梅,丁继辉,宋向东.对求解土性相关距离的空间递推平均法的分析与改进[J].河北农业大学学报,1999,22(1):85-89.
[4]丁继辉,宇云飞,张庆宏,等.土性相关距离计算的非线性曲线拟合法[J].勘察科学技术,2000(3):13-16.
[5]程强,罗书学,高新强.相关函数法计算相关距离的分析探讨[J].岩石力学,2000,21(3):281-283.
[6]刘春原.基于GIS系统的岩土参数随机场特性研究[D].天津:天津大学,2003.
[7]姚若军.土性参数空间变异和相关情况下的土坡可靠度分析[D].武汉:武汉大学,2005.
[8]郭怀志,彭大鹏.材料性能的随机场特性参数的检定方法[J].岩土工程学报,1994,16(3):21-29.
[9]宋向东,任建华.土工参数随机场模型中相关函数的选择[J].数理统计与管理,2007,26(5):773-775.
[10]尹利华,王晓谋,张留俊.天津软土土性指标概率分布统计分析[J].岩石力学,2010,31(2):462-468.
