混沌系统同步性质的一个注记

徐玉华，李坤花，周武能

(1.东华大学信息科学与技术学院，上海201620;2.郧阳师范高等专科学校 数学与财经系，湖北 十堰442000，3.济源职业技术学院基础部，河南济源454650)

0 前言

1 状态反馈同步控制

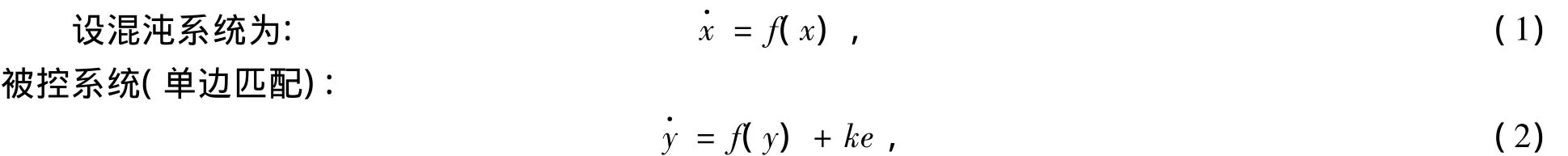
由于混沌系统是有界的，因此，对于混沌系统，下面的假设是容易满足的［4］。

假设1 对于混沌系统，假设 f(y)－f(x)≤ly－x，其中l＞0。

由式(1)和式(2)，得到误差系统:

当l+k≤0时，V·≤0，根据Lyapunov稳定性理论，当时间t趋于0时，误差e趋于0。把式(1)和式(2)的单边匹配变成如下的双边匹配，即:

事务处理模块 事务处理模块主要包括用户事务和系统事务两部分，其中用户事务主要包括对用户信息的处理；而系统事务主要包括对播放器进行一些逻辑控制，如暂停、播放、截图等操作。

则式(4)误差系统仍为式(3)，即:

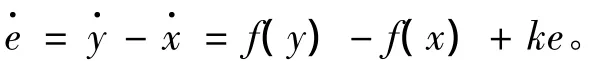
显然，单边匹配和双边匹配系统同步的条件相同，尽管单边匹配和双边匹配所得到的误差系统一样，但是仿真结果表明它们达到同步的时间不一样。

下面以文献［13］中的混沌系统为例:

由于混沌系统是有界的，根据文献［14］，l=50，由 l+k≤0取k=－51，取系统初值分别为(10，30，3)，(5，17，19)，用无量纲误差来比较两种方法收敛的速度。从图1可知:单边匹配比双边匹配收敛的更快一些。通过仿真还可知:双边匹配已经改变了系统的混沌特性(见图2)，而单边匹配仍保持了系统的混沌特性(见图3)。

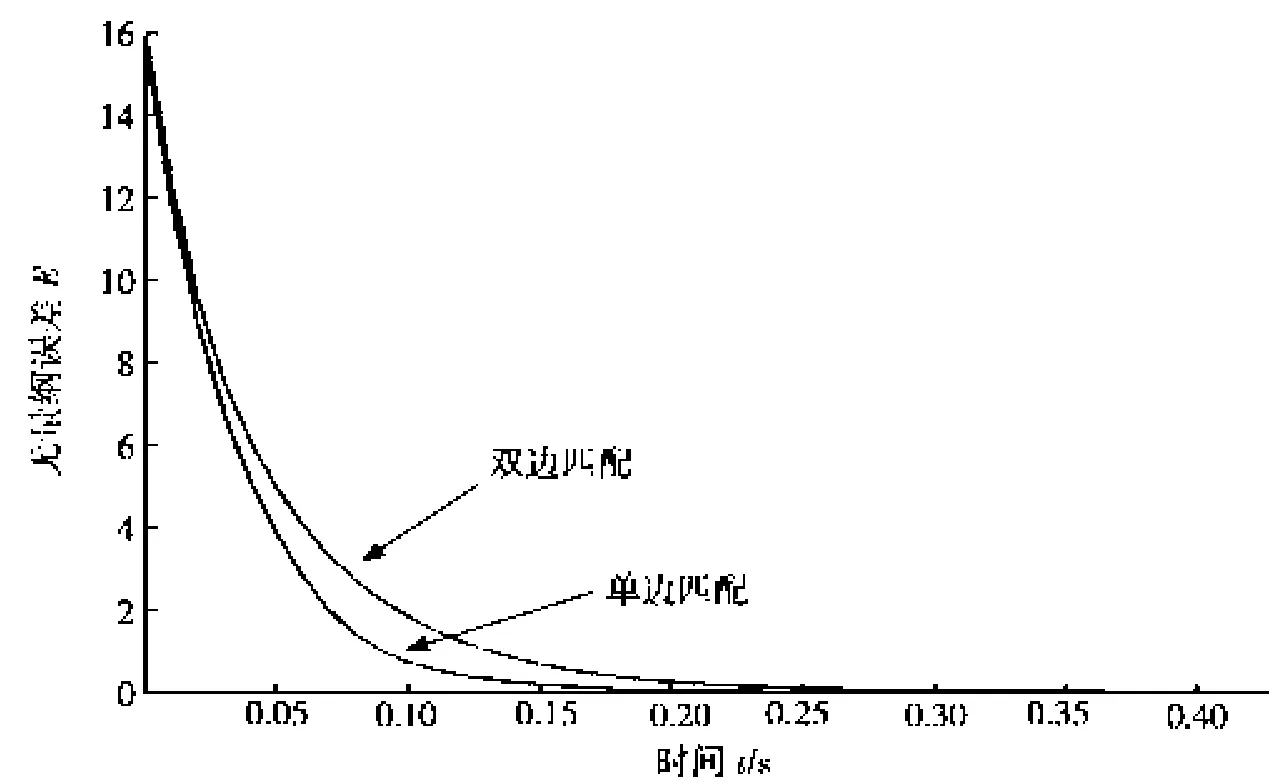
图1 无量纲误差E随时间的演化图

2 自适应反馈同步控制

下面用自适应控制方法得

到类似于上述用状态反馈同步控制方法所得到的结论，值得一提的是，用自适应控制方法对于某些混沌系统，控制器ke可能仅仅只包含一个或者两个自适应反馈控制器就可以实现同步。

对于单边匹配，有:

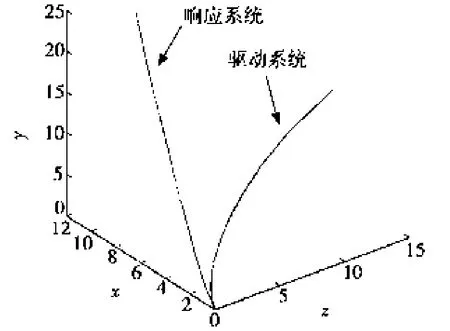
图2 双边匹配时驱动系统和响应系统在无量纲x-y-z轴上的相图

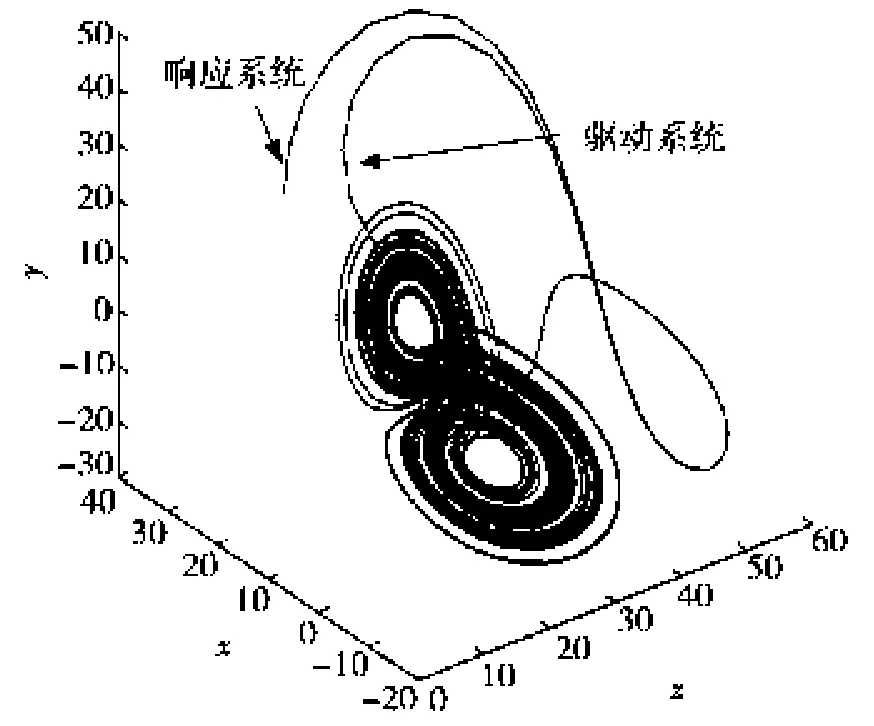
图3 单边匹配时驱动系统和响应系统在无量纲x-y-z轴上的相图

那么误差系统为:

构造如下Lyapunov函数:

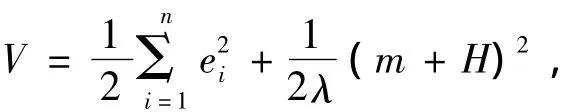
其中H≥nL。则:

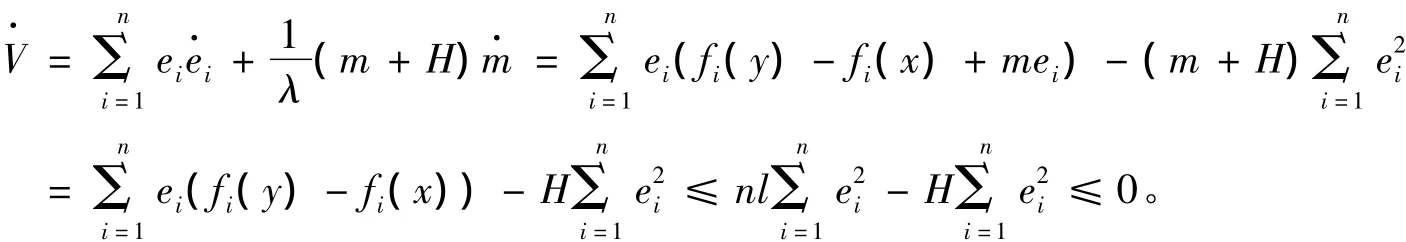
下面举例说明对某些混沌系统，控制器me可能仅仅只包含一个或者两个自适应反馈控制器就可以实现同步。

例1 Lorenz混沌系统［15］:

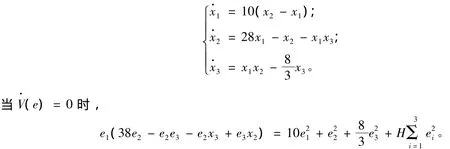
显然，假如e1=0，那么e2=0，e3=0，因此，可取me=m(e1，0，0)，即只需一个自适应反馈控制器。设 λ =8，即= －。

在仿真中，取系统初值分别为(10，2，3)，(5，17，9)，由于m是自适应变量，可取它的初值为1。用无量纲误差来比较两种方法收敛的速度。从图4可知:单边匹配比双边匹配收敛的更快一些。通过仿真还可知:双边匹配已经改变了系统的混沌特性(见图5)，而单边匹配仍保持了系统的混沌特性(见图6)。

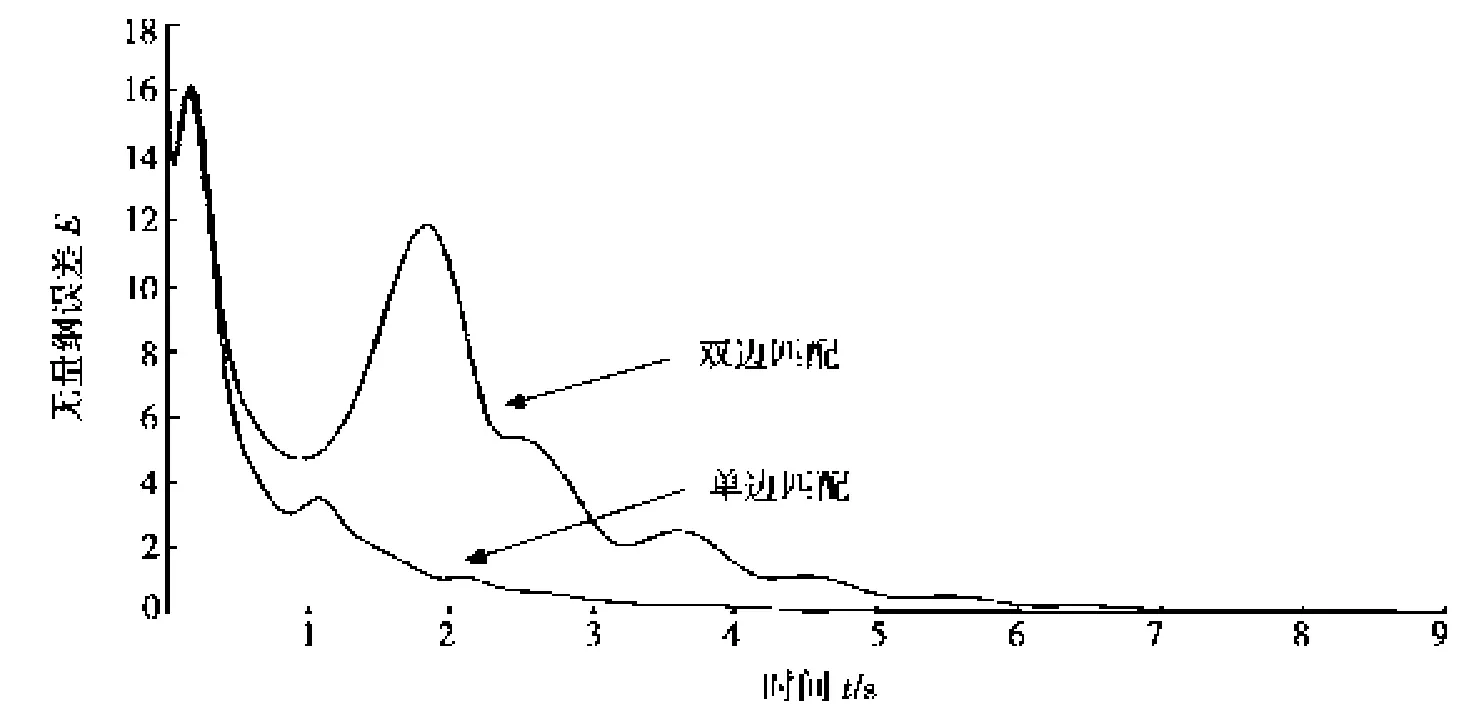
图4 无量纲误差E随时间的演化图

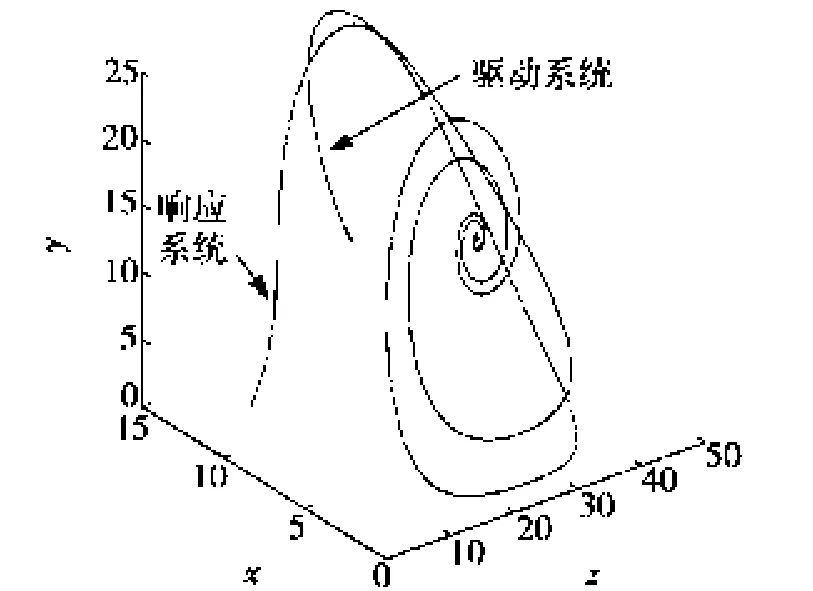
图5 双边匹配时驱动系统和响应系统在无量纲x-y-z轴上的相图

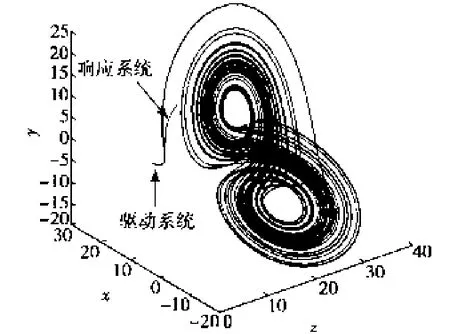
图6 单边匹配时驱动系统和响应系统在无量纲x-y-z轴上的相图

例2 Rikitake混沌系统［16］:

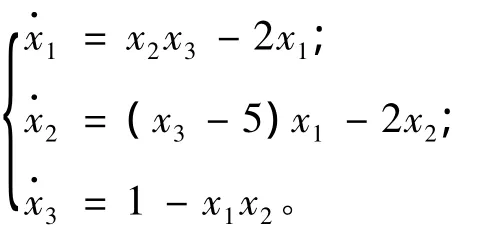
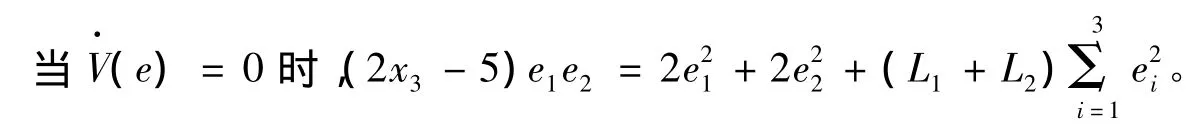
显然，假如e1=0，e3=0，那么e2=0，因此，可取me=m(e1，0，e3)，即只需两个自适应反馈控制器。设 λ =8，即= － 8(e21+e23)。

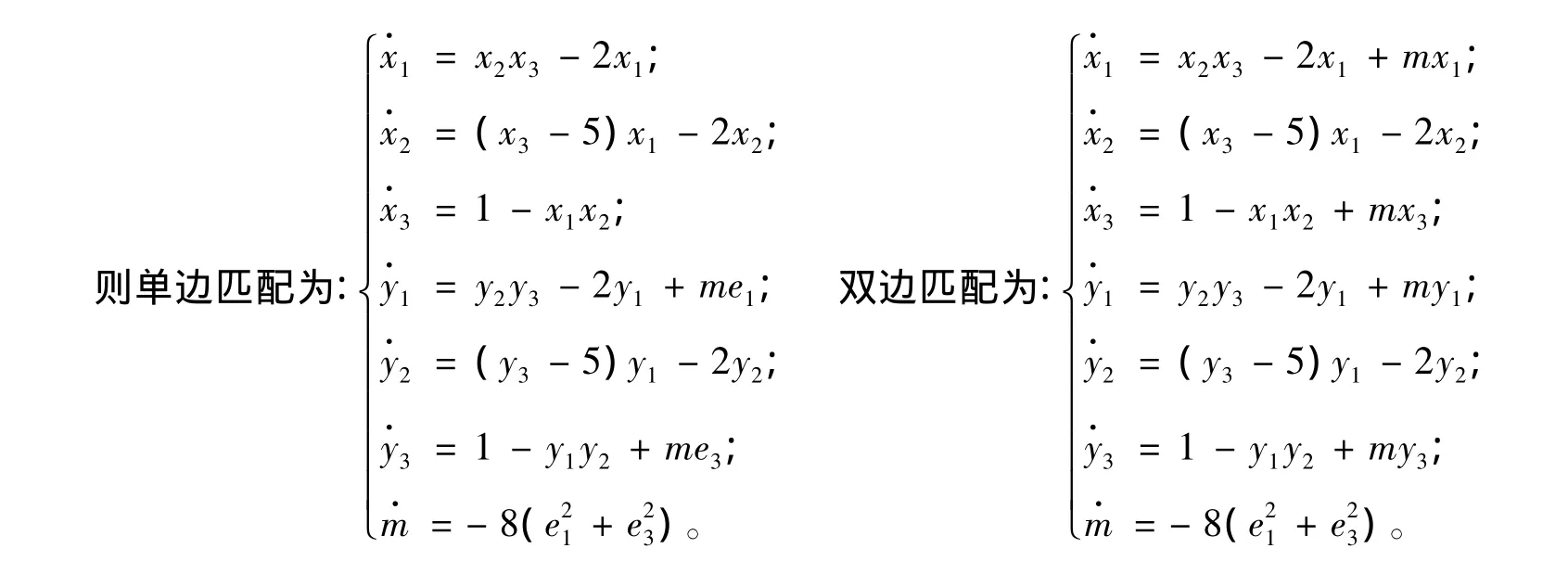
在仿真中，取系统初值分别为(3，2，3)，(5，1，8)，由于m是自适应变量，可取它的初值为1。用无量纲误差来比较两种方法收敛的速度。从图7可知:单边匹配比双边匹配收敛的更快一些。通过仿真还可知:双边匹配已经改变了系统的混沌特性(见图8)，而单边匹配仍保持了系统的混沌特性(见图9)。

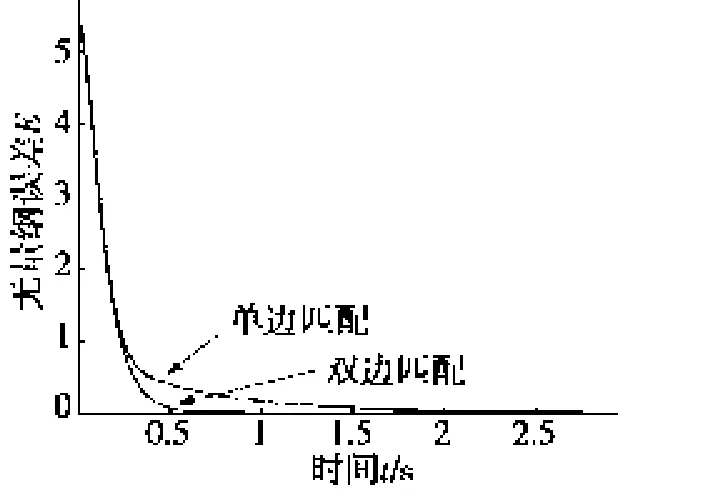
图7 无量纲误差E随时间的演化图

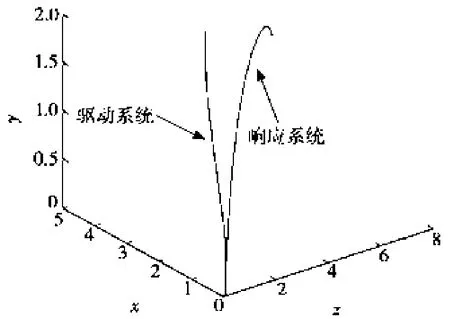
图8 双边匹配时驱动系统和响应系统在无量纲x-y-z轴上的相图

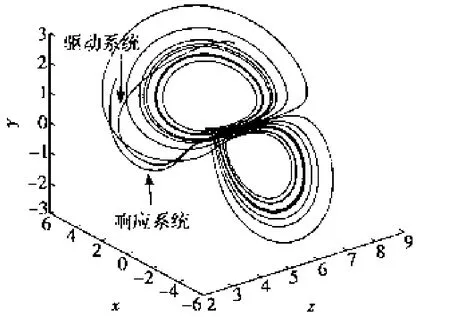
图9 单边匹配时驱动系统和响应系统在无量纲x-y-z轴上的相图

3 结论

本文把单边匹配响应系统的控制器分解成两部分分别匹配到驱动系统和响应系统(双边匹配)时，得到双边匹配的误差系统与单边匹配的误差系统完全相同。仿真发现:两种匹配方法系统达到同步的时间不一样，并且双边匹配改变了系统的混沌特性，而单边匹配仍保持了系统的混沌特性。

［1］Pecora L M，Carroll T L.Synchronization in Chaotic Systems［J］.Physical Review Letters，1990，64(6):821 －824.

［2］Elabbssy E M，Agiza H N，Eldessoky M M.Adaptive Synchronization of a Hyperchaotic System with Uncertain Parameter［J］.Chaos Solitons ＆ Fractals，2006，30(5):1133 －1142.

［3］吕金虎，陆君安，陈士华.混沌时间序列分析及其应用［M］.武汉:武汉大学出版社，2002:25－38.

［4］陈关荣，吕金虎.Lorenz系统族的动力学分析控制与同步［M］.北京:科学出版社，2003:98－106.

［5］Lü J H，Lu J A.Controlling Uncertain Lü System Using Linear Feedback［J］.Chaos Solitons＆ Fractals，2003，17(1):127－132.

［6］Wu X J，Wang H，Lu H T.Hyperchaotic Secure Communication Via Generalized Function Projective Synchronization［J］.Nonlinear Analysis，2011，12:1288 －1299.

［7］Zhou P，Zhu W.Function Projective Synchronization for Fractional-order Chaotic Systems［J］.Nonlinear Analysis，2011，12:811－816.

［8］Zhang L P，Jiang H B.Impulsive Generalized Synchronization for a Class of Nonlinear Discrete Chaotic Systems［J］.Commun Nonlinear Sci Numer Simulat，2011，16:2027 －2032.

［9］胡爱花，吴昌应.基于脉冲控制的不确定混沌系统的同步［J］.河南科技大学学报:自然科学版，2010，31(5):51－55.

［10］Liu G M，Ding W.Impulsive Synchronization for a Chaotic System with Channel Time-delay［J］.Commun Nonlinear Sci Numer Simulat，2011，16:958 －965.

［11］Zhao X S，Li Z B，Li S.Synchronization of a Chaotic Finance System［J］.Applied Mathematics and Computation，2011，217:6031－6039.

［12］Xu Y H，Zhou W N，Fang J A，et al.Adaptive Lag Synchronization and Parameters Adaptive Lag Identification of Chaotic Systems［J］.Physics Letters A，2010，374(34):3441 －3446.

［13］Lü J H，Chen G R.A New Chaotic Attractor Coined［J］.International Journal of Bifurcation and Chaos，2002，12(3):659－661.

［14］Li D M，Lu J A，Wu X Q，et al.Estimating the Global Basin of Attraction Andpositively Invariant Set for the Lorenz System and a Unified Chaotic System［J］.J Math Ana Appl，2006，323(2):844 －853.

［15］Lorenz E N.Deterministic Nonperiodic Flow［J］.Journal of Atmospheric Sciences，1963，20(2):130 －141.

［16］Rikitake T.Oscillations of a System of Disk Dynamos［J］.Proc Cambridge Philos Soc，1958，54:89－105.