高饱和度土的一维连续方程及其固结分析
2011-08-11徐浩峰谢康和
徐浩峰,谢康和
(1.浙江大学 软弱土与环境土工教育部重点实验室,杭州310027;2.浙江大学宁波理工学院,浙江 宁波315100)
通常认为水面(或地下水位)以下的土是饱和土。而实际上水面下的天然土往往含有气泡,并不一定完全饱和;比如湖海底的沉积土以及泥炭土等中可能含有甲烷等有机气体形成的大小气泡[1],另外对某地区软土的勘察,百余项地质勘察报告均显示软土的饱和度并非100%,一般大于94%[2]。虽然如此,工程上往往按饱和土来处理的[3]。但是这类高饱和度土的固结压缩特性与完全饱和土的固结特性是有差异的,比如存在明显的瞬时沉降变形[4-5]。这是因为其前提假设相对于完全饱和土发生了一些变化,比如孔隙流体的压缩性已经不可以忽略。因此对高饱和度土的连续方程和固结方程应重新给予考虑和梳理。
对于饱和土的连续性问题,体积守恒等式是适用的;但当土体是三相体时,体积的守恒式就显得复杂。如对高饱和度土的连续性描述为:在不排水条件下,高饱和度土排出的水气混合物量等于土骨架的压缩量与水气混合物的回弹量之和[6];将水和气看成混合的可压缩流体,提出混合流体的连续性为单位土体体积的压缩量等于排出的流体体积与残存流体压缩量之和[7];土体单元中渗流出的水体积等于孔隙中水体积的变化量[8]等。
可见,对于高饱和度土的体积守恒式从不同的角度有不同的表述方式,这在理解上是困难的。有必要以新的思路来建立连续性方程。对于非饱和土的连续方程,若按体积守恒,建立的困难主要在于气相体积的变化难以把握[9]。不过,如果从质量守恒的角度,则可以避免气相给连续性问题所带来的麻烦,因为气体质量的变化在一般情况下是可以忽略的。
为此,拟建立了一个可变体积的微六面体元,使该微六面体元中的土粒质量不随运动过程而变化,推导出非饱和土体的连续方程。在这个连续方程的基础上,假设有效应力原理仍适用于高饱和度土,引入与太沙基一维固结相类似的假设,建立起了一维固结方程,随后分析讨论了其固结特性。
1 一维连续方程
如图1,取一微六面体元,令土粒质量不随运动过程而变化,于是经体元面迁移的质量仅是混合流体的质量。设孔隙水的密度为ρw,渗流速度为vw;孔隙中气体的密度为ρa,流动速度(与渗流速度类似,也指的是相对于整个截面的假想流速)为va。那么,在z轴方向上,单位时间内流入的质量为(ρwvw+ρava)dxdy,流出的质量为

这里,在z轴方向上的上下边界可能是变动的,即控制体为可变体积,要求速度是相对于边界面的相对速度。上式即为泰勒展开式,当dz为小量的时候才成立。
对于体元内质量的变化,设t时刻该点土体密度为ρ(x,y,z,t)。于是,t时刻体元内质量为ρdxdydz,则单位时间体元内的质量增加为(在压缩过程中dz将随时间发生变化)

根据质量守恒定律,体元内质量的增加等于流入体元的总质量,等式两边消去dxdydz,整理得
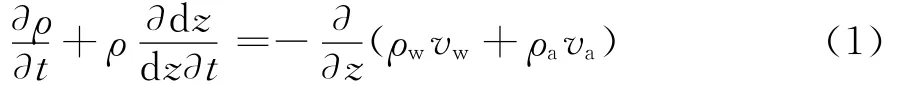
由微元体体积dV=(1+e)dVs,则∂dV=∂edVs,又有dV=dxdydz及∂dV=dxdy·∂dz,所以:

于是,将上式代入式(1),可得

式中,e为土体孔隙比。
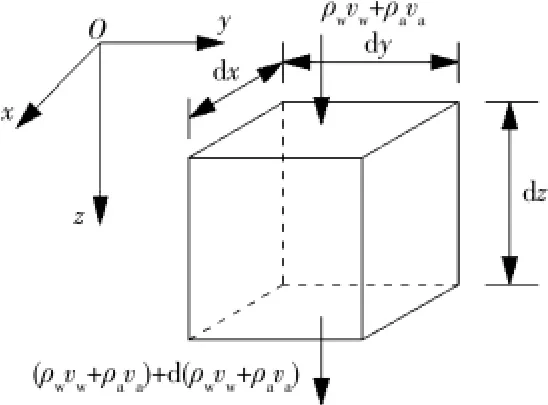
图1 通过可变微六面体元的一维混合流体渗流
若土体颗粒和孔隙水不可压缩,并忽略气体质量,令Sr为土体饱和度,ds为土粒比重,由ρ=ρw(ds+Sre)/(1+e)可得

若水气不相互转化或转化很少(此处假设为等温过程),可忽略排出气体的质量,则
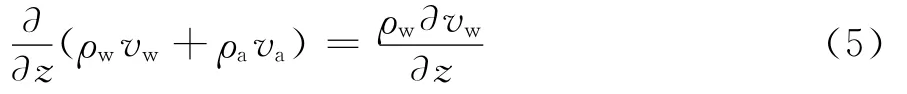
假设孔隙水渗流服从Darcy定律,于是

式中uw为孔隙水压力,k为非饱和土中孔隙水的渗透系数。假定k不随深度变化,上式两边对z求导,将式(4)、式(5)和式(7),代入式(3)得


上式即为忽略气体质量、水流服从Darcy定律的非饱和土体一维连续方程。
2 一维固结方程
2.1 高饱和度土的有效应力公式
严格地说,太沙基有效应力原理仅适用于完全饱和土,因为只有此时孔隙水压力才是一个“中性应力”。而研究非饱和土体,一般采用Bishop于20世纪50年代末提出的试探性的非饱和土有效应力表达式:

对于气相以微小的封闭气泡形式而存在的高饱和度土来说,包承纲[10]指出此时土中基质吸力很小,并且几乎不随饱和度变化。因此,他建议可以将高饱和度土看成具有可压缩性流体的两相土,吸力的作用也可以忽略。限定于以挟气水形式排出而固结的高饱和度土,可被视为是被可压缩流体所饱和的“饱和土”,其有效应力公式可采取如下形式[6、11]:

式中,uaw为孔隙混合流体压力。当气泡可以随孔隙水一起流动时,孔隙混合流体压力可取孔隙水压力[12],即uaw=uw。对此证明如下:设气泡呈球形,则在土体内作一截面,如图2所示。

图2 高饱和度土中一点的截面各相组成及应力
设截面中有n个气泡,所截某一气泡(球半径为Ri)的面积为Aai(圆半径为ri),气泡内气压为uai。对其中任意一个气泡,分析与孔隙水压的关系,表面张力的作用如图3所示(T为表面张力系数)。

图3 气泡所截半径及表面张力的作用
图中可见,ri=Risinθi。又因为

所以

由上式可见,悬浮于孔隙水中的气泡,对混合流体的表观压力没有影响。
对于气相以大气泡的形式而存在的高饱和度土来说,情况是复杂的[13]。
2.2 一维固结方程的推导
由土体体积的变化量dV与土体有效应力关系dV=-mvV∂σ′,有

混合流体体积Vv的变化量与其压力的关系为dVv=-lvVv∂uw。设孔隙水不可压缩,Vw保持不变:
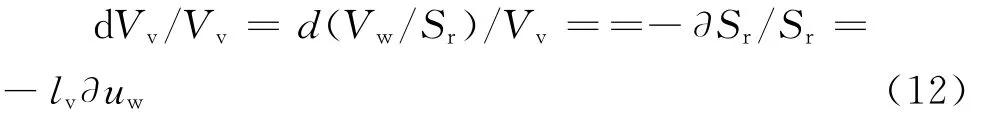
由式(11)和式(12),并结合有效应力公式,代入式(8),可得

若总应力σ不随时间变化,则式(13)可整理为

式中,n为土体孔隙率,n=e/(1+e);mv、lv分别为土体和混合流体的体积压缩系数。
上式即为高饱和度土的一维固结方程。当饱和度Sr=100%时,混合流体即为孔隙水,其体积压缩系数lv=0。于是,上式即可退化为太沙基的一维固结方程。上式亦可记为:

式中,C′v=k/[γwSr(mv+nlv)],即为高饱和度土的固结系数。
2.3 固结方程的求解
取分析土层如图4所示。均质高饱和度淤泥质粘土地基厚度为2H,双面透水。假定:1)外部荷载是一次瞬时施加的;2)固结过程中渗透系数、土体和混合流体的体积压缩系数以及饱和度均为常数(对于非饱和土,在压缩固结过程中饱和度是会变化的,正如土体的渗透系数和土体的压缩系数都会发生改变一样。假设饱和度为常数也为Conte等[14]所采用)。于是,边界条件为:z=0,uw=0(t>0)以及z=2H,uw=0(t>0)。

图4 一维均质土层固结模型
对于初始条件,分析高饱和度土的压缩固结过程:假设在加压瞬时,混合流体来不及排出,荷载将由混合流体和土骨架共同承担,两者发生相同的压缩量。设一土体体积V=Sh(S为截面积,h为厚度)。在加压瞬时产生压缩变形Δhis,则体积压缩量为SΔhis。按土体计算的体积压缩量ΔV1=mvVΔσ′,按孔隙流体计算的体积压缩量ΔV2=lvnVΔuw。因为ΔV1=ΔV2=SΔhis。又由p=Δσ=Δσ′+Δuw,可解得加载瞬时孔隙混合流体的压力增量。于是初始条件为:

由初始条件和边界条件,解式(15)得到任意时刻,任意深度的孔隙水压力的表示式为:

式中,M= (2m-1)π/2,时间因子T′v=C′vt/H2。
任意时刻、任意深度的土体有效应力表示式:

任意时刻地基的沉降为:

任意时刻的地基土层平均固结度U为任意时刻地基沉降Sct与最终总变形量之比:

2.4 参数的确定
固结方程式中的土体体积压缩系数mv可由一维压缩试验得到。混合流体的体积压缩系数lv可由下式计算得到:

混合流体体积压缩系数也可由下式估算[15]:

式中,ua为气泡绝对压强。
对渗透系数k,取与饱和度的三次方成正比[16],有下式:

式中,kw为饱和土孔隙水的渗透系数。
3 算例分析及其讨论
土体孔隙率n=0.50,Sr=95%,渗透系数k=1.10×10-10m/s;土体体积压缩系数mv=4.40×10-4kPa-1,孔隙流体压缩系数lv=0.96×10-4kPa-1。则mv/(mv+nlv)=90.2% ,则由式(17),可得孔隙水压随时间和沿深度的变化曲线,并与饱和情形时相比较,分别如图5和6所示。

图5 不同深度的孔隙水压消散曲线及与饱和土的比较

图6 不同时刻的孔隙水压随深度分布曲线与饱和土的比较
从图5可见,高饱和度土的初始超静孔隙水压力z/H=0.7处和z/H=1.0处都相同uw/p=0.902,小于饱和土时的比值(饱和土的uw/p=1.0);离排水面较近的z/H=0.7处的超静孔隙水压,先于离排水面较远的z/H=1.0处开始消散;当时间因子较大时,饱和土、高饱和度土不同位置处的超静孔压都差别越来越小。在图6中也可以看到,同一时间因子,沿深度分布的超孔隙水压力,高饱和度土的都小于饱和土;另外,其差值也不断缩小,在z/H=1.0处,时间因子Tv=0.1时,其差值为0.09,时间因子Tv=0.5时,其差值为0.04。
由式(20),作固结度与时间因子的关系曲线,如图7所示。可见,高饱和度在瞬时就有9.8%的固结度;但是,随着时间的发展,与饱和土的固结度差别越来越小:当时间因子Tv=0.1时,其差值为6.30%;时间因子Tv=1.0时,其差值为0.67%。

图7 固结度随时间的发展与饱和土的比较
于是,对于高饱和度土,可以认为当时间因子Tv=1.0时固结完成。那么结合式(23),高饱和度土所需时间t′与相应饱和土t之比:

本例中,计算得t′/t=1.23。由式(24),作固结完成时间比与饱和度、土体压缩性的关系曲线,如图8所示。其中,高压缩性土的压缩系数即为上述数值;中等压缩性土的压缩系数取1.0×10-4kPa-1;低压缩性土的压缩系数取4.40×10-5kPa-1。
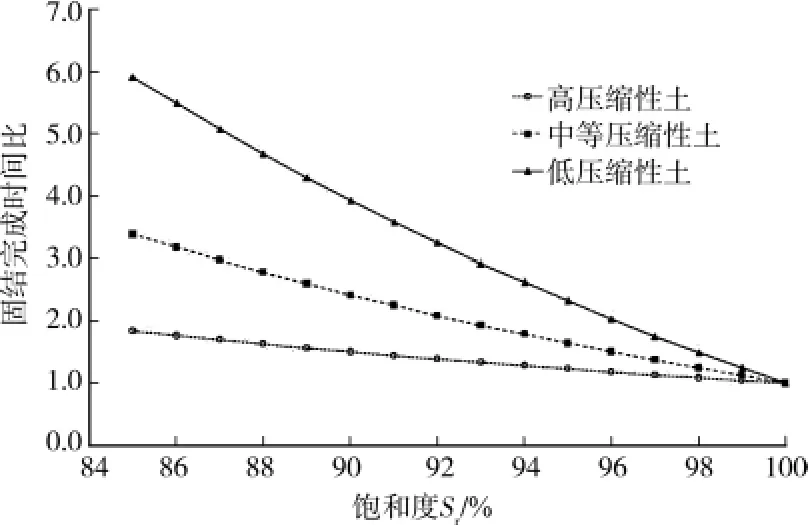
图8 饱和度与固结完成时间比的关系曲线
由上图可见,饱和度越小,固结完成时间比差别越大,近似呈线性的关系。当饱和度为100%时,固结完成时间比即为1;还可以看到土体的压缩性越小,固结完成时间比差别越大。
4 结 论
从质量守恒的角度出发,避免了非饱和土中气相体积难以确定的困难,建立了土体的一维连续方程,推导了高饱和度土的一维固结方程,求解并分析了固结压缩特点。得到的结论如下:
1)从质量守恒的角度分析,可有效地化解建立非饱和土连续性条件的困难。
2)高饱和度土可视为具有可压缩流体的“饱和土”,不过固结系数不同。
3)高饱和度土的固结压缩特点:瞬时超静孔隙水压小于所施加的荷载;从固结度与时间因子的关系曲线上看,虽然前期与饱和土比较时差别较大,但是随后的固结度差距减小,当时间因子为1.0,也可认为固结完成;饱和度越小,土体压缩性越小,高饱和度土的固结完成所需时间与相应饱和土的之比就越大。
[1]MAZUMDAR A,PEKETI A,DEWANGAN P,et al.Shallow gas charged sediments off the Indian west coast:Genesis and distribution[J].Marine Geology,2009,267(1/2):71-85.
[2]刘用海.宁波软土工程特性及其本构模型应用研究[D].杭州:浙江大学,2008:25-60.
[3]周琦,邓志勇,王友元,等.起始水力梯度对真空预压下砂井地基固结过程的影响[J].土木建筑与环境工程,2010,32(2):46-52.ZHOU QI,DENG ZHI-YONG,WANG YOU-YUAN,et al.Effect of initial hydraulic gradient on consolidation of sand-drained ground improved by vacuum preloading[J].Journal of Civil,Architectural & Environment Engineering,2010,32(2):46-52.
[4]朱向荣,李振,王金昌.舟山国家石油储备基地堆载预压加固效果分析[J].岩土力学,2008,29(4):881-886.ZHU XIANG-RONG,LI ZHEN,WANG JIN-CHANG.Analysis of consolidation effects of Zhoushan National Oil Reserve Base improved by preloading combined with plastic drains[J].Rock and Soil Mechanics,2008,29(4):881-886.
[5]CHU J,BO M W,ARULRAJAH A.Soil improvement works for an offshore land reclamation[J].Proceedings of the Institution of Civil Engineers-Geotechnical Engineering,2009,162(1):21-32.
[6]魏海运,詹良通,陈云敏.高饱和度土的压缩和固结特性及其应用[J].岩土工程学报,2006,28(2):264-269.
[7]殷宗泽,凌华.非饱和土一维固结简化计算[J].岩土工程学报,2007,29(5):633-637.YIN ZONG-ZE,LING HUA.Simplified computation of 1Dconsolidation for partially saturated soil[J].Chinese Journal of Geotechnical Engineering,2007,29(5):633-637.
[8]SCOTT R F.Principles of soil mechanics[M].Mass:Addison-Wesly Pub Company,Inc,1963.
[9]张志红,赵成刚,邓敏.非饱和土固结理论新进展[J].岩土力学,2005,26(4):667-672.ZHANG ZHI-HONG,ZHAO CHENG-GANG,DENG MIN.Recent development of consolidaton theories of unsaturated soils[J].Rock and Soil Mechanics,2005,26(4):667-672.
[10]包承纲.非饱和压实土的气相形态及孔隙压力消散问题[C]//第三届全国土力学和基础工程会议论文选集,1979:129-135.
[11]NUTH M,LALOUI L.Effective stress concept in unsaturated soils:Clarification and validation of a unified framework [J].International Journal for Numerical and Analytical Methods in Geomechanics,2008,32(7):771-801.
[12]CHANG C S.Consolidation analysis for partly saturated clay by using an elastic-plastic effective stressstrain model[J].International Journal for Numerical and Analytical Methods in Geomechanics,1983,7:39-55.
[13]SILLS G C,WHEELER S J,THOMAS S D,et al.Behavior of offshore soils containing gas-bubbles[J].Geotechnique,1991,41(2):227-241.
[14]CONTE E, COSENTINI R M, TRONCONE A.Geotechnical parameters from V-P and V-S measurements in unsaturated soils[J].Soils and Foundations,2009,49(5):689-698.
[15]FREDLUND D G.非饱和土土力学[M].陈仲颐.译.北京:中国建筑工业出版社,1997.
[16]YOO C,KIM S.Three-dimensional numerical investigation of multifaced tunneling in water-bearing soft ground[J].Canadian Geotechnical Journal,2008,45:1467-1486.
