一类适用于卫星回传系统的LDPC码的构造方法
2011-08-09刘春江施玉海吴力夫裴育杰
刘春江,施玉海,吴力夫,裴育杰
(国家广播电影电视总局广播科学研究院,北京 100866)
责任编辑:哈宏疆
0 引言
在传统的卫星双向通信系统中,通常采用Turbo码作为卫星回传信道的编码纠错方案[1],并且常采用对重要的控制字段使用码率较低的编码方案而对有效数据载荷采用码率较高的编码方案兼顾数据传输的有效性和可靠性。由Berru等学者提出的Turbo码具有较强的纠错能力,在特定参数的设置下可以达到接近Shannon限的性能[2],然而,Turbo的译码复杂度较高,随着码长的增加呈指数关系增长,并且由于Turbo码自身的特性具有较高的误码平底,严重影响了传输性能,因此在一些新的卫星回传传输方案中采用低密度奇偶校验(Low Density Parity Check,LDPC)码作为前向纠错编码方案[3-4]。
LDPC码是由Gallager于1962年首先提出的[5]。近年来,在Mackay等人的研究中发现LDPC码在编译码复杂度较低的情况下其纠错能力具有接近并有可能超越Turbo码的优点[6],掀起了人们对LDPC码的研究热潮。LDPC码主要分为两类:一类是随机构造的LDPC码,该类码在长码时具有很好的纠错能力,但编码过于复杂、难以用硬件实现,编码时间过长也不利于硬件的实时应用;另一类是结构码,它由几何、代数和组合设计等方法构造。大多数LDPC结构码是循环或准循环结构,准循环码在中短码时具有相当强的纠错能力,性能接近随机构造的最优LDPC码[7-8],又因其硬件实现极其简单,因此具有很好的应用前景[9]。
LDPC码的应用中需要重点解决两方面问题,一是LDPC码的构造问题,二是确定适用高效的编解码算法及其具体实现的问题,前者是基础和前提,本文在探讨总结LDPC码常用构造方法的基础上,提出一种可用于卫星回传的LDPC码的构造方法,并使用仿真工具软件对其纠错性能加以仿真分析。
1 LDPC码常用构造方法
LDPC码是基于稀疏校验矩阵的线性分组码,通常由它的校验矩阵H来定义,设编码后的码长为N,信息位的长度为K,校验位的长度M=N-K,码率R=K/N,则校验矩阵H是一个M×N的矩阵,构造LDPC码实际上就是构造一个稀疏的校验矩阵H。LDPC码的常用构造方法及其特点主要有[10]:
1)LDPC码最早的构造方法是由其发明者Gallager提出的,其构造的是规则LDPC码,该码的检验矩阵H具有如下特性:每行有k个“1”;每列有 j个“1”;记λ为任意两列具有相同“1”的个数,则λ不大于1;k和j与H中的长度和行数相比是很小的。Gallager构造方法的特点是校验矩阵H在水平方向上分为j个子矩阵,每个子矩阵中每列含有单个“1”,第一个矩阵按某种预先决定的方式构造,随后的子矩阵是第一个子矩阵的随机置换。
2)1996年对LDPC码进行再发现的MacKay等人提出了MacKay构造法,该方法是在Tanner引入线性分组码的图形表示法(Tanner图)后基于对图的分析等而设计得出的,又分为两种略有不同的构造法:第一种构造法的特点是每列有固定的列重,随机构造矩阵使其行重分布尽量均匀,且任意两列的重叠不大于1;第二种构造法与第一种类似,但是重量为2的列数最多为M/2。
3)在MacKay构造法的基础上推广获得了UL-A和UL-B构造法:UL-A的构造方法是先是2个(M/2)×(M/2)的单位阵重叠,再是(M/4)×(M/4)的单位阵重叠,依次类推,最终最多M个重量为2的列;UL-B的构造方法与UL-A类似,只是左边部分行重最多为2。
4)Kou和Lin等人从几何的观点研究LDPC码的代数构造方法,提出了基于有限几何的点、线构造LDPC码的有限几何构造法,分别称为有限欧几里德几何(Euclid⁃ean Geometries,EG)构造法和投影几何(Projection Geom⁃etries,PG)构造法,这两类构造法构造的LDPC码是循环和准循环的,具有较好的约束参数和最小码距,这类码一般是规则码,和随机构造的规则LDPC码相比性能上有些损失,但具有更低的误码平底和更低的编码译码复杂度。
5)LuBy等人证明了经过仔细构造的非规则二进制LDPC码性能优于规则码,由此产生了一类统称为非规则构造法的LDPC码构造方法。非规则码校验矩阵中每行重量和每列重量都是非均匀分布的,构造过程中需要先确定每一重量的列期望个数和每一重量的行期望个数,然后寻找性能好的度数分布,最后构造出具有不均匀误码保护能力的非规则LDPC码。
此外还有将校验矩阵H中元素的取值范围由GF(2)改为GF(q)的非二进制构造,由于非二进制构造的LDPC码译码复杂度极高,目前实际应用较少。
2 新的LDPC码构造方法
本文提出将LDPC码用作卫星回传的纠错编码方案,考虑到卫星回传通信中数据帧的长度一般都较短的情况,所采用的LDPC码码长不能太长,但纠错性能却必须要高,同时为了降低译码复杂度以利于降低硬件成本,因此采用完全随机构造的非规则LDPC码和性能有所损失的有限几何构造法或Gallager构造法构造的规则LD⁃PC码都有不小的缺陷,综合考虑常用的LDPC码构造方法及其特点,提出一种伪规则LDPC码的构造方法。
在阐述该构造方法之前,首先对涉及到的字母的含义进行说明:H代表校验矩阵,Hx代表校验矩阵的子矩阵x,N代表编码后的码长,K代表编码前的码长,即信息位长度,M代表校验位的长度,R代表编码码率,m为K的一个约数,用于控制分块的大小,m越大,将H分块数量越少。构造LDPC码时,首先生成一个M行N列的全“0”元素矩阵H,然后根据参数m对校验矩阵H进行分块,将校验矩阵拆分为M行M列的子矩阵H0和M行K/m列的子矩阵H1,H2,…,Hm,如图1所示。

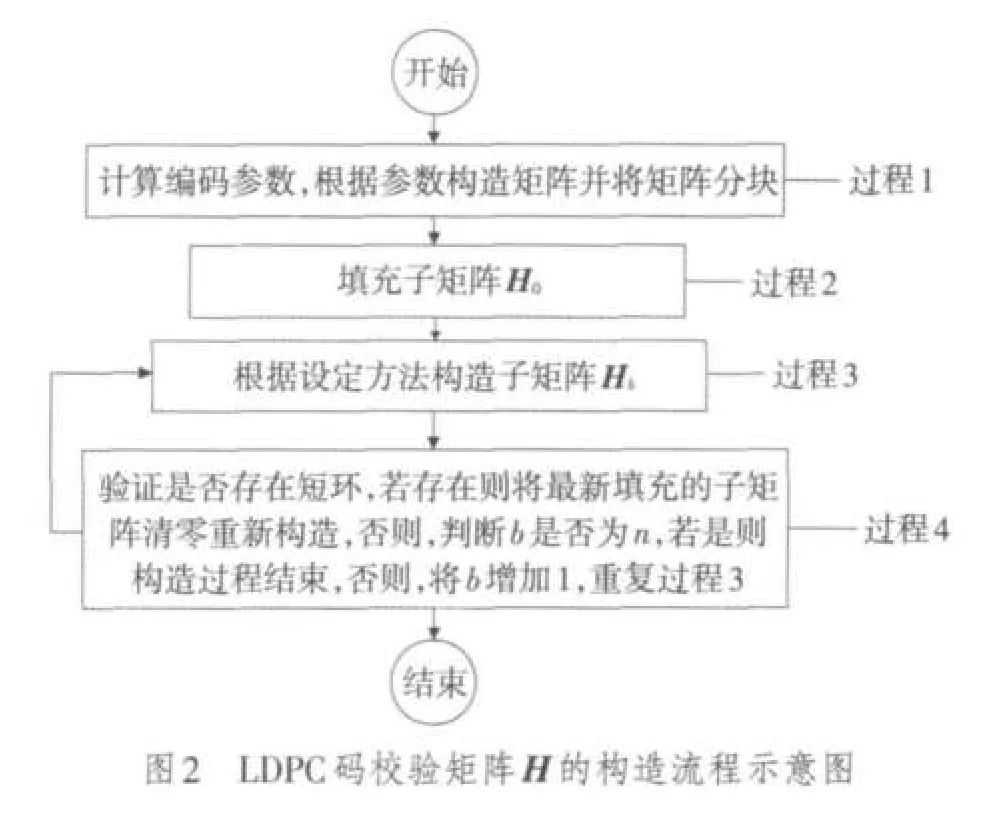
随后按照以下步骤逐步构造LDPC码的校验矩阵:1)将H0中主对角线和主对角线下方次对角线所在的位置填充为1,将作为子矩阵下标的变量b初始值设置为1;2)尝试填充子矩阵Hb,b=1,2,…,m,该子矩阵的列重为dv(b),不同的子矩阵具有不同的列重,下述表述中省略参数b;3)生成dv维随机向量V,该随机向量的每个元素vi互不相等,且满足1≤vi≤M;4)在子矩阵内,先填充该子矩阵的第1列,在第一列的填充位置标记为v1,v2,…,vi;5)确定上述子矩阵内第j列的填充位置为(vi+j×m)mod M,其中i=1,2,…,dv;6)验证由H0,H1,H2,…,Hb构成的矩阵内是否存在短环,如果存在短环,那么将最新填充的Hb清零,重新回到步骤2,如果不存在短环,继续步骤7);7)如果b=m,那么构造过程结束,否则将b增加1后继续从步骤2)执行。
上述LDPC码的构造过程可归结为图2所示流程。
3 仿真分析及结论
采用上述LDPC码构造方法设计构造了一个用于卫星回传通信的码长为2112、码率为0.5的LDPC码型,使用Matlab仿真软件,对所设计的LDPC码和相近长度的Turbo码在AWGN信道条件下进行误码率仿真分析,获得如图3所示的误码率曲线示意图。

由图可见,采用该方法构造的LDPC码具有与同等长度的Turbo码相近的误码率性能,但是却具有更低的误码平底,更加适合于卫星回传信道的数据传输。
另外,该LDPC码的构造方法能够适用于码长为从1000左右的短码到码长为十几万的长码,构造的校验矩阵具有一定的循环性,能够极大地降低校验矩阵的存储空间,此外,采用本文所述方案构造的LDPC码的性能接近随机构造的LDPC码的性能,提高了LDPC校验矩阵的性能,在通信系统中具有较强的实用性。
[1]DVB.ETSIEN 301790,V1.2.2,Interaction channelfor satellite distribution systems[S].2000.
[2]BERRU C,GLAVIEUX A,THITIMAJSHIMA P.Near Shannon limit error-correcting coding and decoding:Turbo-codes[C]//Proc.of IEEE ICC’93.[S.l.]:IEEE Press,1993:1064-1070.
[3]ETSIEN 302307 v1.1.1(2005-03)[S/OL].[2010-04-01].http://www.dvb.org/documents//en302307.v1.1.1.draft.pdf.
[4]ETSIEN 302307 V1.1.2(2006-06)[S/OL].[2010-04-01].http://www.s2licensing.com/assets/documents/DVS2standard.pdf.
[5]GALLAGER R G.Low-density parity-check codes[J].IRE Trans.Information Theory,1962(8):21-28.
[6]MACKAY D J C.Good error correcting codes based on very sparse matrices[J].IEEE Trans.Inform.Theory,1999,45(3):399–431.
[7]BRESNAN R.Novel code construction and decoding techniques for LDPC codes[D].Cork,Ireland:Dept.ofElec.Eng.,UCC,2004:128-148.
[8]TANNER R M.Spectralgraphs for quasi-cyclic LDPC codes[C]//Proc.2001 IEEE InternationalSymposium on Information Theory,Washingtion DC:IEEE Press,2001.
[9]刘春江,吴智勇,于新,等.一类准循环LDPC码的快速编码方法[J].电视技术,2007,31(6):11-13.
[10]张忠培,史治平,王传丹.现代编码理论与应用[M].北京:国防工业出版社,2007.
