林下可燃物含水率预测的一个多项式气象模型1)
2011-08-09叶更新叶希莹
叶更新 叶希莹
(吉林省通化市气象局,通化,134001)
森林可燃物含水率的大小对于森林火灾具有重要影响,是确定森林火险等级的决定性因素。利用气象要素估计和判断含水率的多少,进而对火险发生的可能性作出判断是个有意义的工作,早在20世纪20年代,美国就对森林可燃物的含水率与气象要素之间的联系进行了观测研究,Weidman R H在1923年研究了森林可燃物的含水率、相对湿度等气象要素与林火之间的关系,指出天气预报和可燃物的状态对于火险预报都是必须考虑的因素[1]。Gisborne H T利用Peirst River林业实验站的资料[2],分析了处于3种不同环境中的含水率的变化及其与易燃程度的联系。这些早期工作为人们建立科学的火险等级预报做出了开创性贡献。近些年来,我国的很多学者通过大量的试验和理论分析,研究了森林可燃物含水率与气象要素之间的联系,并利用统计方法建立了很多预测模型。杜秀文等[3]分析了不同种类可燃物与多种气象要素的联系,说明了气象因子影响含水率的显著性、复杂性。杨美和等[4]通过大量试验数据研究了可燃物含水率同自身的引燃性的相互关系,并提出含水率预测方程的一元非线性函数形式。居恩德等[5]分析了可燃物含水率与气象要素之间的相互关系、建立了细小可燃物的气象预测方程,并利用可燃物含水率对森林燃烧等级进行了划分。王瑞君[6]等根据野外定点资料和雨后点火试验,将燃烧等级进行了划分。张广英等[7]利用多元线性回归方法建立了伊春市五营林场的可燃物含水率方程,并进行了检验。高永刚等[8]引入森林可燃物含水率气象预测模型,并划分了森林火险气象指数在伊春林区森林火险等级预报中的应用指标值。王超等[9]研究了含水率随时间变化的动态规律;以当日气象因子中的温度、湿度与连续无降水日为自变量,利用多元统计的方法建立了3种可燃物类型的含水率回归方程。这些研究对于人们认识气象要素与林火之间的关系具有启发作用,所建立的气象模型为人们预测森林可燃物含水率提供了有效的工具。以往这些工作大多是建立在线性回归模型基础上的,而线性模型在应用过程中存在一定问题。首先是准确率的问题,尽管模型的计算结果通过了统计检验,但总体上来说,实况与计算值的误差较大(见文中的分析),其次,在因子的选择上依赖于相关系数,这就造成了不同季节采用不同的因子,这种情况在统计学上有一定道理,但从物理机制上却不好解释。事实上,森林可燃物的含水率与气象要素之间的关系极其复杂,不可能是简单的线性关系,而是非线性的关系,因此,在方程中引入非线性项具有很好的理论和实践意义。文中将分别建立线性和多项式含水率气象要素预测模型,并对两者的表现进行比较和分析。
1 材料与方法
林下可燃物含水率资料来自通化市测站的资料,该测站选取通化市南部的八队前山、夹皮沟、驮道岭3个固定观测地点,分别进行山地阴坡山腰、山地阳坡山腰和山脚、山地阳坡山腰和山脊等不同位置的观测,共6个测点,具体位置和林中乔木类型见表1。资料日期从2006年春季开始至2010年春季结束,每年在3—6月份和9—11月份日期尾数为2的那天进行观测,这样的时间间隔基本上为10 d,除去一些无法观测的天数,共64 d,这样得到有效样本为64×6个。

表1 通化市森林可燃物观测点的地理位置和林中乔木类型
气象资料来自通化市气象站的观测资料,包括:日平均温度、日平均相对湿度、日最高温度、日平均风速、降水量、蒸发量、日照时数及累计无降水天数等8个要素(表2)。
文中采用多元线性回归和多元多项式回归2种方法分别对3种地形的含水率(取2测点的平均)建立气象预测模型,并进行对比分析。判断模型拟合优度用调整后的复决定系数[10]146:

式中:n为样本数;k为因子数;R为相关系数。

表2 通化市各个测点与通化气象站要素的相关系数
2 多元线性回归模型
2.1 含水率与气象要素的关系
气象要素与森林可燃物含水率的相互关系是人们重点关注的问题,因为,通过研究二者的联系,能够使人们认识森林可燃物变化的内在机制,并且规范的、大量的常规气象资料能够弥补含水率观测资料的不足。通过数学方法建立准确可靠的含水率预测模型,进而作出客观的火险等级预报,并为护林防火提供科学依据是进行林下可燃物含水率观测的主要目的。以下利用通化市气象站的常规观测资料分析气象要素与林下可燃物含水率的相互关系。
利用多元线性回归建立可燃物含水率预报方程是目前普遍采用的方法,文献[3]—[9]都采用的此种方法,其基本过程是首先选取与含水率相关性较好的要素作为预报因子,然后,再利用多元回归方法求出相应的方程系数。文中也采取这样步骤建立含水率的气象要素多元线性回归模型。表2是通化市八队前山等各个测点与通化气象站要素的相关系数,从表2中可以看出,对于阴坡的2个测点(即测点1、2取平均值),含水率与平均温度、最高温度、前3 d的累积降水量、蒸发量、日照时数都有很好的相关性,其相关系数都通过了0.05的信度检验,特别是最高温度通过了0.01的信度检验,而与相对湿度、无降水日数、风速的相关性不大;对于阳坡山脚—山腰的2个测点(测点3、4),含水率只与最高温度、前3 d累积降水量和日照时数的相关性通过了0.05的相关检验,与其他要素的相关性都不大。对于阳坡山腰—山脊的2个测点(测点5、6)而言,含水率与最高气温、相对湿度、前3 d累积降水量、蒸发量、日照时数和无降水天数等6个要素都有很好的联系,而与平均气温和风速关系不大。
2.2 多元线性回归模型
基于以上的相关分析,分别选取通过0.05相关检验的要素作为预报因子。
对于测点 1、2,选取 x1、x2、x3、x4、x55 个要素,采用最小二乘法求的如下方程:

其复相关系数为0.469 2,调整后的复决定系数为0.152 9;F值为 3.388 3;F0.01=3.36。
对于测点3、4,选取最高温度x2、前3 d累积降水量x4和日照时数x6作为预报因子,得到如下方程:

其复相关系数为0.477 7;调整后的复决定系数为0.189 6;F值为 6.110 9;F0.01=4.98。

图1 多元线性回归模型含水率预测值和实况观测值的曲线图
对于测点 5、6,选取 x2、x3、x4、x5、x6、x76 个要素作为预报因子,得到如下方程:

其复相关系数为0.531 1;调整后的复决定系数为0.206 5;F值为 3.863;F0.01=3.16。
从以上结果看,3个观测地点的预测方程都通过了0.01信度的F检验,但总体上看复相关系数不高,最大的只有0.531 1,而最大的调整后的复决定系数仅为0.206 5,说明预测曲线与实况曲线存在较大差异。这种差异可能来自多方面的影响,线性模型本身是一个近似的统计关系,允许存在一定的误差,另外,含水率变化具有复杂性以及影响因素的多样性,可能有些重要影响的因素没有考虑而导致误差的存在;还有在相互关系的形式上,一些非线性因素没有考虑在方程中,也是导致误差存在的原因之一。
3 多项式多元回归模型
3.1 多项式模型的基本描述
以上所描述的线性模型是在因子与要素之间线性假设的前提条件下完成的。实际上因子与对象之间的关系极其复杂,大多数情况下无法表达成1种解析的形式,在一些合理的假设下利用统计方法建立观测值之间的相互联系是目前使用的主要方法。文献[6]—[9]利用线性模型建立了气象要素与含水率之间的联系,取得了很好的效果,文中所建立的线性模型也都通过了必要的信度检验,统计学上讲可以作为预测林下可燃物含水率的方法来使用。但在实际上因子与预测对象之间不可能是单一的线性关系,更可能的则是一种非线性的关系,因此,利用非线性方法建立的数学模型可能比线性模型更为接近实际情况。这里我们不妨假设含水率为多个非线性函数的线性迭加,即有如下的函数表达式:

式中:xj为因子,也就是说,含水率由n个包含单一因子的非线性函数迭加而成。
对于任何形式的函数,只要满足其具有无穷阶导数和余项在项数为无穷时为零2个条件,总可以展开成如下的幂级数的形式:

式中:在级数的各项中,当幂越大,系数越小,为分析方便,在一定精度的条件下,对(6)式取有限项,此时函数变为多项式形式,即:

对于多要素影响情况下,含水率可以表达为如下形式:

式中:W为含水率;b0为常数;xj为第j个因子;i为自然数幂;b(i,j)为系数。
文中共选取表2中的8个因子,即有n=8;对于m的选取,采取预测与实况的比较而言进行。一般情况下,随着因子的增加,相关系数或决定系数会变大,但却掺进了一些虚假的成分[10]146。因此,在选择因子时,用调整后的复决定系数和F值对最大幂指数进行选取。表3是不同最大幂指数(m)情况下相关系数及对应的R2a和F值,从表3中可以看出,随着最大阶数的增大,相关系数在逐渐变大,由1阶时的0.548增加到7阶时的0.822,但调整后的复决定系数却呈现出另外的变化形态,开始随着m的增大而变大,在m=3时达到最大,为0.408,之后随着幂指数的增大,R2a却在变小;m=5时=0.067;而m=6、m=7时已经为负值。相应的F值也呈现了相同的变化趋势,F在m>3以后,相关系数增加缓慢,而F值却减小很快,到m=5时,已经无法达到0.05的检验标准。根据R2a和F值的变化,m=3是最佳取值,这时调整后的复决定系数最大,而相对应的F值也很大,实际上已经通过0.01 的 F 检验标准(此时的 F0.01=2.26)。
表3 不同最大幂指数情况下6个测点平均含水率与多项式模型的复相关系数(R)、调整后的复决定系数()及相应的F值

表3 不同最大幂指数情况下6个测点平均含水率与多项式模型的复相关系数(R)、调整后的复决定系数()及相应的F值
m 因子数 R R2a F F0.05 1 8 0.548 0.199 2.951 2.16 2 16 0.676 0.272 2.472 1.86 3 24 0.796 0.408 2.810 1.79 4 32 0.807 0.291 1.809 1.80 5 40 0.812 0.067 1.114 1.91 6 48 0.816 -0.403 0.623 2.16 7 56 0.822 -1.988 0.260 3.01
3.2 计算结果分析
文中选取表2列出的8个因子作为基本因子,利用(8)式作为含水率预测的多项式模型,最大幂指数取3,即有m=3,n=8。图2列出了模型的计算结果,通过与图1比较可以看出曲线得到了明显的改善,表4、表5列出了模式的一些定量指标。
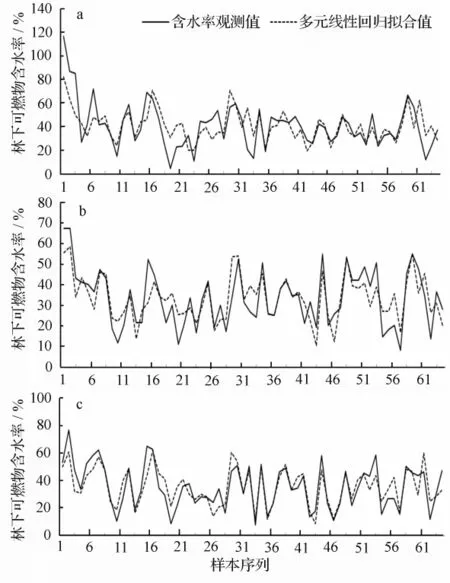
图2 多元多项式回归模型含水率与预测值、观测值的曲线图
表4为多项式模式不同测点的方程系数及相应的检验,从表4中可以看出,与线性模型比,实况和预测值的相关系数有了很大提高,线性模型在3个地点的复相关系数分别为0.469 2(测点 1、2)、0.477 7(测点 3、4)、0.531 1(测点 5、6);多项式模型在3个地点的复相关系数分别为0.6919(测点1、2)、0.7989(测点 3、4)、0.851 8(测点 5、6),分别提高了 0.222 7、0.321 2、0.320 7,平均提高了0.288 2;多项式模型在3个地点调整后的复决定系数分别为 0.157 9(测点 1、2)、0.415 6(测点 3、4)、0.556 7(测点5、6),比线性模型的0.1529(测点1、2)、0.1896(测点 3、4)、0.206 5(测点 5、6)分别提高了 0.005 0、0.226 0、0.350 2,平均提高了0.193 7,因此,多项式模型在预测含水率变化趋势上更加接近实况。当然,3个地点的模型与实况值的相关性还是存在差别的,测点3、4和测点5、6都通过了0.01的F检验,但地点1、2没有通过0.05的信度检验。

表4 最大幂指数为3时不同测点的方程系数及相应的检验
表5是2个模型与实况的绝对误差对比表,从表5中可以看出,多项式模型的绝对误差比线性模型的明显偏小,平均误差减小了30.368%,其中测点5、6减小的幅度最大,达到42.535%,测点1、2最小,为15.554%,这与调整后的复决定系数的提高是一致的。

表5 2个模型与实况的绝对误差对比
与线性模型最大的区别就在于多项式模型在因子的选择上的同一性,而不是拘泥于因子与对象的线性相关性,线性回归则要考虑这样的因素,甚至在同一地点的不同时期都要选取不同的因子[7-9],对于不同的测点文中采用了同样的预报因子,因为因子与预测对象相互联系的内在机制应该具有同一性,因此,多项式模型的这种选取比线性模型的选取的意义更为清晰。
另外,多项式模型的计算结果与线性方程系数有很大不同,对于线性模型,系数的符号与相关系数的符号相同,见式(2)~(4),最高气温在方程中总是为负,但多项式因子前的系数不再有此特点,比如最高温度一阶系数就为两负一正。
4 结论与讨论
森林可燃物是森林燃烧的物质基础,也是林火行为的主体,可燃物含水率的大小与森林燃烧的难易程度密切相关。利用通化市森林可燃物6个观测点的观测资料,分析了林下可燃物含水率与气象要素之间的相互联系,结果发现,含水率与最高气温、前3 d累积降水量、蒸发量、日照时数有很好的相关性,根据相关分析的结果分别对不同测点建立了含水率的线性和多项式气象模型,对2种模型进行了比较,结果表明,多项式模型比线性模型与实况的相关性有很大提高,线性模型在3个地点的复相关系数分别为0.4692(测点1、2)、0.4777(测点3、4)、0.531 1(测点5、6);多项式模型在 3 个地点的复相关系数分别为 0.691 9(测点1、2)、0.7989(测点3、4)、0.8518(测点 5、6),分别提高了 0.222 7、0.321 2、0.320 7,平均提高了0.288 2;多项式模型在3个地点所得调整后的复决定系数分别为 0.157 9(测点1、2)、0.415 6(测点3、4),0.556 7(测点5、6),比线性模型的 0.152 9(测点 1、2)、0.189 6(测点 3、4)、0.206 5(测点5、6)分别提高了0.0050、0.226 0、0.3502,平均提高了0.193 7,平均绝对误差减小了30.368%。因此,多项式模型比线性模型在描述气象要素与含水率的相互关系上更为合理。
[1]Weidman R H.Relation of weather forcasts to the prediction of dangerous forest fire conditions[J].Monthly Weather Review,1923,51(11):563-564.
[2]Gisborne H T.Using weather forecasts for predicting forest-fire danger[J].Monthly Weather Review,1925,53(2):58-60.
[3]杜秀文,李茹秀,王英杰.几种森林类型可燃物含水率与气象因子关系的分析[J].东北林业大学学报,1988,16(3):87-90.
[4]杨美和,高颖仪,宋嘉宝,等.森林可燃物含水率的测试与分析[J]吉林林业科技,1990,85(2):28-29.
[5]居恩德,陈贵荣,王瑞君.可燃物含水率与气象要素相关性的研究[J].森林防火,1993(1):17-21.
[6]王瑞君,于建军,郑春艳.森林可燃物含水率预测及燃烧性等级划分[J].森林防火,1997(2):16-17.
[7]张广英,高永刚,曹晓波,等.伊春市五营森林可燃物含水率预测模型初步研究[J]安徽农业科学,2007,35(36):11956-11958.
[8]高永刚,张广英,顾红,等.森林可燃物含水率气象预测模型在森林火险预报中的应用[J].中国农学通报,2008,24(9):171-175.
[9]王超,高红真,程顺,等.塞罕坝林区森林可燃物含水率及火险预报[J].林业科技开发,2009(3):59-62.
[10]何晓群,刘文卿.应用回归分析[M].2版,中国人民大学出版社,2007:146.
