基于平移不变剪切波变换的医学图像融合*
2011-08-02王雷李彬田联房
王雷 李彬 田联房
(华南理工大学自动化科学与工程学院,广东广州510640)
基于多尺度分解的医学图像融合方法的核心问题之一是多尺度分解工具的选择.小波变换是最典型的多尺度分解工具[1].然而,二维离散小波变换只能将图像分解为水平、垂直、对角3个高频子带,这使其只能捕获有限的方向信息,因此,基于小波变换的融合方法由于小波不能很好地表示图像中的线、边缘、轮廓等高维信息而会导致伪影现象.剪切波是为克服小波的缺点而提出的一种新颖的多尺度几何分析工具.相比图像融合中常用的其它多尺度分解工具,如曲线波变换[2]、轮廓波变换[3]、非下采样轮廓波变换 (NSCT)[4]等,剪切波变换具有其自身的优势.从近似理论的观点来看,剪切波形成一个具有小波形式的多尺度多方向的紧支集结构,它是图像信号(如边缘)的真正的二维稀疏表示,目前只有曲线波具有类似的性质.然而,曲线波的实现过程过于复杂,并且不能在图像的多分辨分析框架内实现.相比轮廓波和NSCT,虽然剪切波变换具有相似的实现过程,但是剪切波在剪切过程中没有方向数目和支撑基尺寸大小的限制.此外,剪切波逆变换只需对正向变换中的剪切滤波器进行加和处理,而不需要像轮廓波变换和NSCT那样对方向滤波器逆合成,这说明剪切波的实现过程具有更高的计算效率.目前,剪切波变换已经被应用于遥感图像的融合中,并取得了良好的效果[5-6].然而,在上述文献中,剪切波变换的离散化过程通过下采样策略实现,由于其不具备平移不变的性质而易产生伪吉布斯现象.
基于多尺度分解的医学图像融合方法的另一个核心问题是频域系数的融合规则.待融合图像进行多尺度分解后,低频系数表示图像的近似逼近,高频系数代表图像的细节信息.传统的低频取平均策略易降低融合图像的对比度.对于高频融合,基于人工神经网络的融合策略近年来越来越受到学者们的重视,如脉冲耦合神经网络[7-8].但是在这些应用中,神经网络包含许多参数,需要专家依靠经验去设置,这限制了它们的使用范围.自生成神经网络(SGNN)是一类特点鲜明的自组织神经网络,它不需要外在参数的设定,因而具有自主性高的优点[9-10].但是上述文献中的基于SGNN的图像融合方法是直接对图像的像素进行聚类,只考虑了图像灰度值的变化,其本质是将待融合图像像素的灰度值聚类后进行加权处理,因而可能导致融合后的图像产生块状效应.基于上述分析,文中提出一种基于平移不变剪切波变换的医学图像融合新方法.
1 基于平移不变剪切波变换的融合方法
文中提出的基于平移不变剪切波变换的医学图像融合方法主要包括3步:(1)将图像进行多尺度的平移不变剪切波分解,获得图像的频率子带;(2)对低频系数采用基于区域系数绝对值和权重的融合规则进行处理;对于高频系数,在每个高频子带,计算其支持向量值,将支持向量值输入到SGNN中进行聚类分析,根据聚类结果确定融合后图像的高频系数;(3)通过逆平移不变剪切波变换重建融合后的图像.文中待融合的图像记为A和B,融合后的图像记为F,具体过程如图1所示.
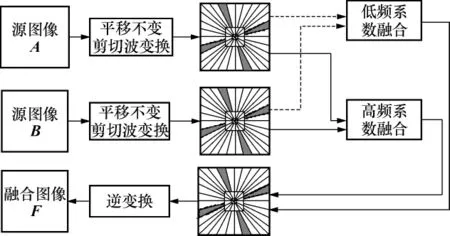
图1 基于平移不变剪切波变换的医学图像融合算法示意图Fig.1 Schematic diagram of medical image fusion algorithm based on shift-invariant shearlet transformation
1.1 图像的平移不变剪切波变换
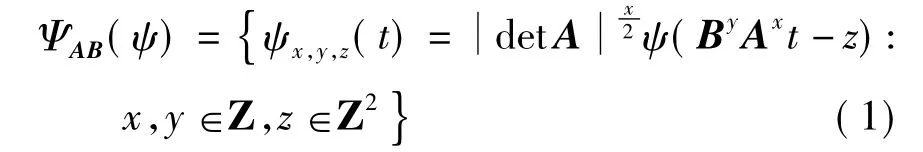
式中:ψ∈L2(R2),L表示可积空间,det表示矩阵的行列式;A称为各向异性膨胀矩阵,A=
平移不变剪切波变换[11]的离散化过程主要分为两步:多尺度剖分和方向局部化.多尺度剖分是通过非下采样的金字塔滤波器组[12](NSPF)实现的,每一级需要对上级中所采用的滤波器按矩阵D=进行上采样,图像经过d级非下采样塔式滤波,可以得到d+1个与源图像大小相同的子带图像.
方向局部化是通过剪切滤波器(SF)完成的.标准的剪切波变换中使用的剪切滤波器是在伪极化网格中通过窗函数的平移操作实现的,其过程需要下采样,因而不具有平移不变性.平移不变的剪切变换把标准的剪切滤波器从伪极化网格系统映射回到笛卡尔坐标系统.通过逆傅里叶变换,可以证明其操作可以直接通过二维卷积完成(参看文献[11]定理3.1),避免了下采样操作因而具有平移不变性.其具体过程又称为Meyer窗口的构建.

图2 离散的平移不变剪切波变换示意图Fig.2 Schematic diagram of discrete shift-invariant shearlet transformation
令j表示图像分解的尺度,j=1,2,…,M,平移不变剪切波变换的具体过程如图2所示,可描述为:
(1)利用非下采样金字塔策略将图像fj分解成为低通图像fj+1和细节图像gj+1;
(2)针对细节图像gj+1,构建Meyer窗口进行多尺度剖分;
(3)对各个方向子带进行逆傅里叶变换得到平移不变剪切波系数cj+1.
剪切波满足抛物线尺度,对某尺度子带图像进行l级平移不变剪切波方向分解,可得到2l+2个与原始输入图像尺寸大小相同的子带图像.因此,对图像j级分解后,可得到个子带图像,其中,J表示图像分解层数,lj是在尺度j下的方向分解级数.图3给出了图像Lena分解成2层的实例.

图3 图像Lena的两层离散的平移不变剪切波分解示例Fig.3 Illustration of decomposing image Lena into 2 levels by discrete shift-invariant shearlet transformation
经过平移不变剪切波分解后,每一个剪切波位于近似大小为22j×2j、线方向斜率为2-jl的梯形对上,如图4(a)所示.根据小波理论,由一维小波张成的二维小波基具有正方形的支撑区间,在尺度j,其近似边长为2j,如图4(b)所示.当尺度j变大时,小波支撑基的面积随之变大,但是由于其无方向性,非零的小波系数以指数形式增长,导致大量不可忽略的系数出现.小波逼近奇异曲线最终表现为图5(a)所示的“点”逼近过程,它不再是原曲线最优的稀疏表示.剪切波以图5(b)所示的近似长条形即梯形对去逼近曲线,当尺度j变大时,其支撑基的线方向斜率2-jl也随之变化,使得这种近似长条形的支撑基具有各向异性,能够有效捕获方向信息,它是图像中边缘等特征的真正的稀疏表示.这一性质对于医学图像中病变部位的表示、提取具有重要意义.
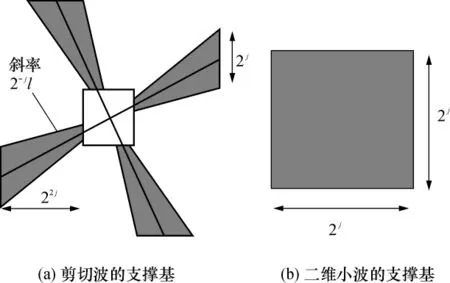
图4 剪切波与小波的支撑基比较Fig.4 Comparison of the support bases for shearlet and wavelet

图5剪切波与小波逼近曲线Fig.5 Curves for shearlet and wavelet representations
1.2 低频系数融合
为避免降低融合图像的对比度,文中采用如下基于区域系数绝对值和权重的融合规则.
(1)计算低频系数在3×3邻域的绝对值的和:
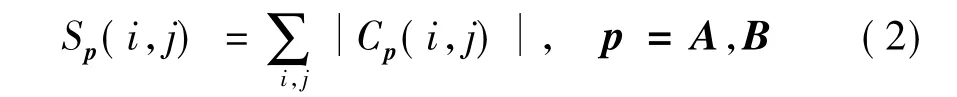
式中,Cp(i,j)表示图像p在(i,j)处的低频系数.
(2)计算系数的权重:
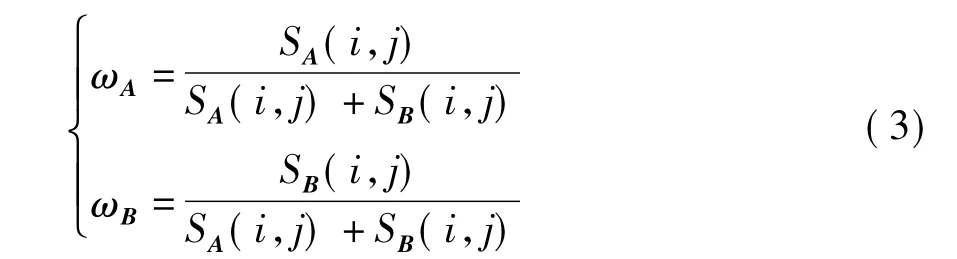
(3)计算融合图像在(i,j)处的低频系数:
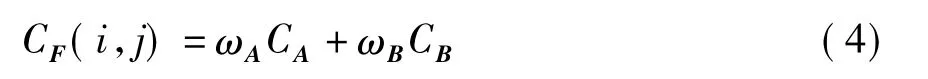
1.3 高频系数融合
SGNN是自组织神经网络的一个扩展,样本通过非监督学习形成一棵包括神经节点、节点间联系、节点权重的自生成神经树(SGNT),具有自主性高、学习速度快的优点.为了充分利用SGNN的优点在高频子带获取更多的特征信息,文中将支持向量机引入SGNN,提出一种基于支持向量值激励的SGNN高频子带融合策略.把每个高频子带系数的支持向量值(T)作为其高频特征,支持向量值的大小反映了高频特征的显著性.令表示图像分解后第l层、第k方向位置为(i,j)的高频子带系数,基于支持向量值激励的SGNN高频子带融合方法的具体步骤如下.
(1)计算两幅图像每个高频子带的支持向量值:
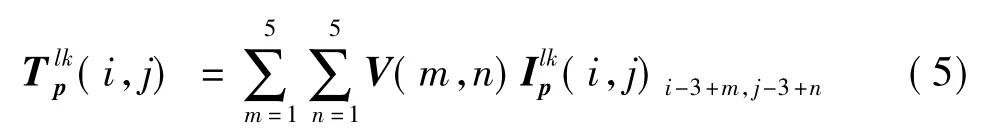
式中,V为支持向量值滤波器,其取值参见文献[13].
(2)将支持向量值输入到SGNN中进行聚类分析,生成SGNT:

式中,c是以Nnode为根节点的所有叶子节点的个数;
(3)对产生的SGNT进行水平修剪和垂直修剪.
(4)聚类结果模糊化:由于图像的差异,在两幅图像高频子带的同一位置的支持向量值可能属于不同的类,因此引入模糊隶属度函数,每一个支持向量值不再属于特定的某一类,而是以一定的模糊隶属度值属于某一类,则在位置(m,n)处的支持向量值q(m,n)属于第j类的隶属度函数为
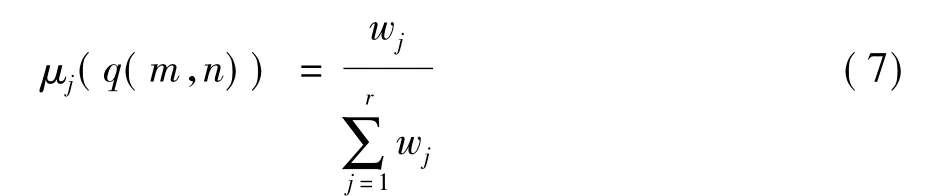
式中,wj是第j类的权重值,r为分类的总数.
(5)融合后图像的高频子带系数为
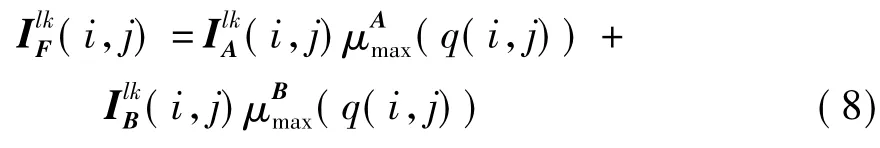
2 实验结果及分析
文中通过3组实验验证所提方法的融合性能.实验1比较了文献[5]中所用的剪切波变换与文中提出的基于平移不变剪切波变换的方法在相同融合规则下的融合性能,结果表明文中方法可以有效地克服伪吉布斯现象.实验2通过对肺部的计算机断层扫描(CT)图像与正电子发射扫描(PET)图像融合来验证文中方法的有效性.实验3在相同融合规则下比较了平移不变剪切波变换与NSCT的融合性能,结果表明平移不变剪切波具有很高的计算效率.实验中平移不变剪切波分解层数为4,所有图像的大小为256×256,并在融合前都已经完全配准对齐.实验平台为Matlab7.4,计算机主机配置为:Intel(R)处理器,CPU主频1.0GHz,内存512MB.
实验中对SGNN、小波变换法(Wavelet)、轮廓波变换法(Contourlet)和NSCT 4种方法分别从熵(EN)、互信息(MI)、平均梯度(AvG)、QAB/F4 个方面[14]与文中方法进行了比较.熵的大小反映了融合图像包含的信息量的多少;互信息反映了融合图像从源图像获取信息的多少;平均梯度表示图像的清晰度,反映了图像对微小细节反差表达的能力;QAB/F值越大表明融合后图像的边缘信息越丰富.在实验中用Shearlet表示文献[5]中基于剪切波变换的融合方法.
2.1 剪切波与平移不变剪切波融合结果比较
图6(a)是核磁共振(MRI)图像,其亮度与组织中氢原子数目有关,图中显示的是软组织.图6(b)是CT图像,它的亮度与组织的密度有关,图中清晰显示的部分是骨架.图6(c)与6(d)分别是使用剪切波与平移不变剪切波图像融合结果.图6(e)与6(f)是融合图像图6(c)和6(d)减去图6(a)得到的残差图像.如图6(b)所示,大矩形所标记处是一个突出的尖点部位,在这个突出点周围灰度值变化剧烈,可近似看作是一个奇异点.由于剪切波变换不具有平移不变性,在奇异点处会产生伪吉布斯现象,图像在奇异点处的特征就不能很好地被捕获,导致融合后的图像会丢失部分特征信息,如6(e)中的矩形标记所标记.对比图6(f)与6(e)可知,平移不变剪切波变换能够有效抑制伪吉布斯现象,捕获更多的原始图像中的特征信息.此外,图6中的小矩形标记部分的差异是平移不变剪切波融合性能优于剪切波的又一个有力例证.

图6 剪切波变换与平移不变剪切波变换的融合结果比较Fig.6 Comparison of fusion results obtained by shearlet transformation and shift-invariant shearlet transformation
2.2 肺部CT-PET图像融合
肺部CT-PET图像融合结果如图7和表1所示.图7(a)是原始CT图像,它显示的是人肺部的组织形态结构,图7(b)是原始PET图像,它描述了肺的对应位置的功能状况,图7(c)-7(h)是各种方法的融合图像.
通过对比融合结果可以发现,图7(c)丢失了大部分的CT图像的信息,融合图像非常不清晰.这主要是因为SGNN融合方法本质上是对两幅待融合图像的像素加权求和处理,而PET图像的像素灰度值取值范围是0~32767,CT图像的像素灰度值取值范围是0~4095.PET图像的像素取值范围远大于CT图像像素的取值范围,简单的加权求和处理必然会降低图像的对比度.图7(d)边缘出现模糊现象,这主要是由于小波变换只能获取图像的“点”奇异信息,对边缘、轮廓等不能很好地表示造成的.图7(e)的边缘出现了明显的伪影现象.由表1可知,就所选用的4个评价指标而言,文中方法优于Contourlet和NSCT.由Shearlet和文中方法的结果对比可知,文中所用的融合方法能够获取更多源图像中的信息.造成这种差异的主要原因是文中方法所用的平移不变剪切波不仅可以克服伪吉布斯现象的产生,而且不同于文献[5]中仅仅考虑单个系数的绝对值的融合规则,文中提出的融合策略充分考虑了高频子带的特征信息,利用支持向量值表征高频特征的显著性,用SGNN自动对支持向量值进行聚类分析,减少了外在人为因素的干扰,有利于高频特征信息的获取,因而更加有效.
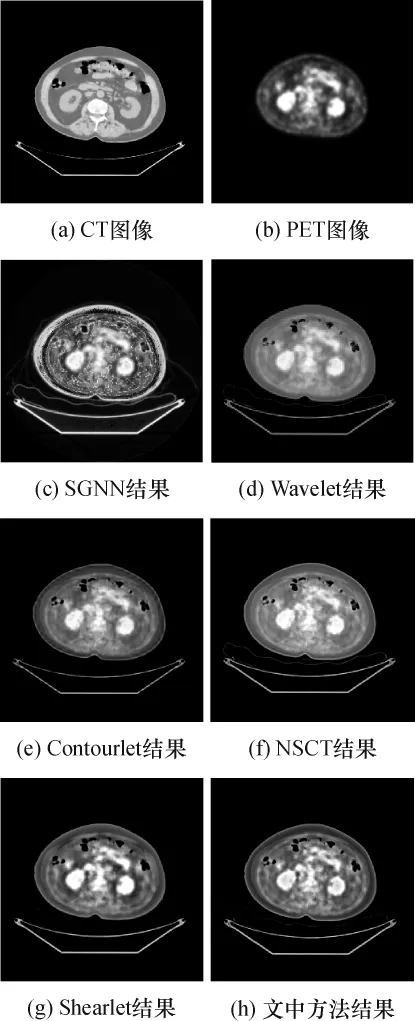
图7 肺部CT-PET图像融合结果Fig.7 Fusion results of the CT-PET image of lung
2.3 文中方法与NSCT融合性能的比较
近年来,NSCT由于能够克服轮廓波变换不具备平移不变性的缺点而被广泛应用于图像融合中,并且被证明是有效的,如文献[4]与[15].因此,将文中提出的基于平移不变剪切波方法的融合性能与NSCT进行了比较.为方便起见,融合规则是低频取平均,高频取绝对值最大,这样避免了过多的融合运算的时间消耗,突出了变换本身的时间消耗.实验中,分解层数都设为4,平移不变剪切波和NSCT的尺度向量分别为(3,3,4,4) 和 (0,1,3,4),NSCT 的多尺度分解和方向剖分滤波器类型分别为“9-7”滤波器和“pkva”滤波器.实验结果如图8和表2所示.

表1 CT-PET图像融合结果量化比较Table 1 Quantitative comparison of fusion results for CT-PET image
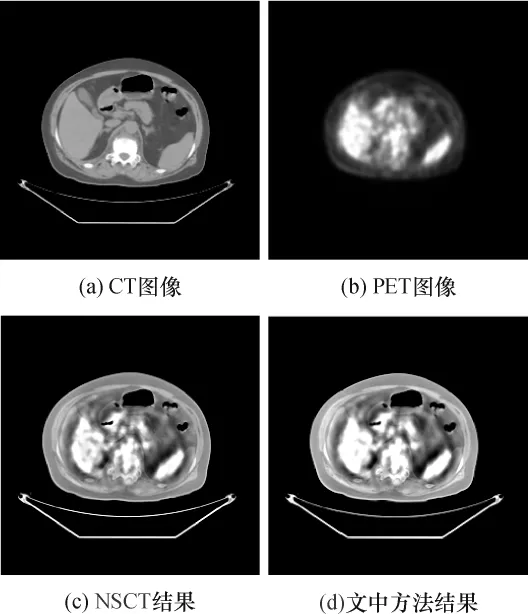
图8 平移不变剪切波变换与NSCT的融合图像Fig.8 Fusion images of shift-invariant shearlet transformation and NSCT
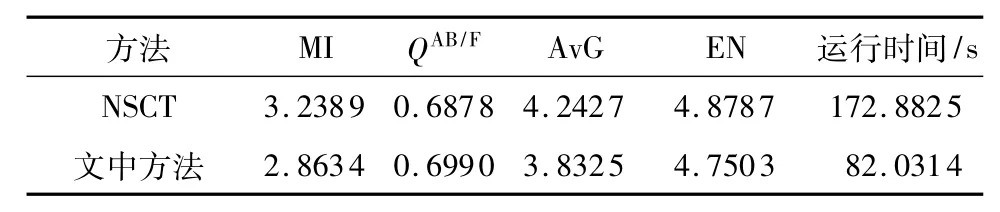
表2 文中方法与NSCT融合结果的量化比较Table 2 Quantitative comparison of fusion results obtained by the proposed method and NSCT
由图8(c)和8(d)可见,CT图像中的形态信息和PET图像中的功能区域都很好地显示在融合后的图像中.从表2也可知两者具有相似的融合性能.但是,从时间消耗来看,NSCT方法所用时间是平移不变剪切波方法的2倍多,这说明虽然具有类似的平移不变性,但是NSCT方法是以高时间消耗为代价的.造成这种差异的主要原因是:NSCT的逆变换过程需要对方向滤波器组重新进行逆合成,而平移不变剪切波则只需对正向变换的剪切滤波器进行简单的加和处理即可完成,具体的细节可以参见文献[11].虽然降低时间消耗可以通过快速发展的计算机硬件技术的改进实现,但是平移不变剪切波方法以其高计算效率无疑为实践中海量数据的融合提供了另一种选择.
3 结语
基于平移不变剪切波变换,文中提出一种医学图像融合方法.相比于传统的基于剪切波变换的融合方法,文中提出的方法可以有效地克服伪吉布斯现象,并具有很高的计算效率.相比于传统的融合规则,文中所用的低频子带的融合规则充分考虑了医学图像的特点;而对高频子带融合而言,支持向量值激励的自生成神经网络方法比直接对图像进行像素聚类分析可以提取更多的高频特征信息,因而融合效果更好.对融合图像的比较和融合结果的量化分析表明:平移不变剪切波不仅可以被用于医学图像融合,而且相比小波等其它常用的多尺度几何分析工具,具有更大的优越性.因此基于平移不变剪切波变换的医学图像融合方法具有广阔的应用前景.
[1]李彬,田联房,陈萍,等.基于模块化设计的三维医学图像体绘制方法[J].华南理工大学学报:自然科学版,2006,34(1):77-81.Li Bin,Tian Lian-fang,Chen Ping,et al.Volume rendering of 3D medical image based on modularization[J].Journal of South China University of Technology:Natural Science Edition,2006,34(1):77-81.
[2]Candues D,Donoho D L.New tight frames of curvelets and optimal representations of objects with piecewiseC2singularities[J].Communications on Pure and Applied Mathematics,2004,57(2):219-266.
[3]Yang L,Guo B L,Ni W.Multimodality medical image fusion based on multiscale geometric analysis of contourlet transform [J].Neurocomputing,2008,72(3):203-211.
[4]Li T J,Wang Y Y.Biological image fusion using a NSCT based variable-weight method [J].Information Fusion,2011,12(2):85-92.
[5]Miao Q G,Shi C,Xu P,et al.A novel algorithm of image fusion using shearlets[J].Optics Communications,2010,284(6):1540-1547.
[6]Deng C Z,Wang S Q,Chen X.Remote sensing images fusion algorithm base on shearlet transform[C]∥Proceedings of the 2009 International Conference on Environmen-tal Science and Information Application Technology.Banff:ACM,2009:451-454.
[7]Wang Z B,Ma Y D.Medical image fusion based on m-PCNN [J].Information Fusion,2008,9(2):176-185.
[8]Yang S M,Wang M,Lu Y,et al.Fusion of multiparametric SAR images based on SW-nonsubsampled contourlet and PCNN[J].Signal Processing,2009,89(12):2596-2608.
[9]Qin Z,Bao F M.A novel image fusion method based on SGNN [J].Lecture Notes in Computer Science,2005,3497(821):747-752.
[10]Jiang H,Tian Y F.Fuzzy image fusion based on modified self-generating neural network [J].Expert Systems with Applications,2011,38(7):8515-8523.
[11]Easley G,Labate D,Lim W-Q.Sparse directional image representations using the discrete shearlet transform[J].Applied and Computational Harmonic Analysis,2008,25(1):25-46.
[12]Da Cunha A L,Zhou J P,Do M N.The nonsubsampled contourlet transform:theory,design,and applications[J].IEEE Transactions on Image Processing,2006,15(10):3089-3101.
[13]Zheng S,Shi W Z,Liu J,et al.Multi-source image fusion method using support value transform [J].IEEE Transactions on Image Processing,2007,16(7):1831-1839.
[14]Qu G,Zhang D L,Yan P F.Information measure for performance of image fusion [J].Electronic Letters,2002,38(7):313-315.
[15]Li S T,Yang B,Hu J.Performance comparison of different multi-resolution transforms for image fusion[J].Information Fusion,2011,12(2):74-84.
