不确定非完整AGV的自适应反演滑模控制*
2011-08-02叶锦华李迪叶峰赖乙宗
叶锦华 李迪 叶峰 赖乙宗
(华南理工大学机械与汽车工程学院,广东广州510640)
由于(t)也是有界的,则W(t)是一致连续的,根据
自动导向车(AGV)是移动机器人的一个重要分支,是现代化生产及物流系统的重要设备,主要用于储运各种物料,在工业、邮政、医疗服务等多个领域有着广泛的应用前景,因此,对AGV的相关技术进行研究具有重要的意义.轨迹跟踪(TT)是AGV运动控制的核心内容之一,是AGV进行其它活动的基础,与路径跟随(PF)不同,TT要求实时跟踪按时间变化的参考目标轨迹,而PF的路径独立于时间变量,所以TT的控制更为复杂;此外,受非完整约束的轮式AGV本质上是非线性的欠驱动无漂移动力学系统,经典线性光滑反馈控制无法直接应用于此类系统,其轨迹跟踪控制相当困难.
轨迹跟踪控制是AGV的关键技术之一,以往大多数控制器[1-2]仅考虑AGV的运动学静态约束模型,而较少考虑其动力学动态特性,这些控制器都建立在低速轻载的前提下,在实际应用中往往无法达到所需的跟踪精度.虽然有些控制器[3-4]考虑了AGV的动力学特性,但由于AGV动力学系统具有强耦合、多输入、多输出的特征,无法获得系统的精确模型,存在不确定性和可变外部扰动,使得常规控制器抗干扰能力不足,轨迹跟踪效果不理想.鉴于此,文献[5]设计了一种结合模型参考和增益调度的自适应控制器,该控制器对系统大的噪声和干扰具有强适应性,但控制器仅适用于路径跟随控制.文献[6]结合前馈逆控制和周期更新的状态反馈控制设计混合跟踪控制器,同时对输入参考轨迹进行递归凸再规划,实现对系统干扰和未建模部分的适应性,但该方法未考虑系统的动力学特性.文献[7]设计了一种自适应比例微分(PD)控制器,该控制器仅针对AGV变载荷参数的情况,对不确定系统的适应性有限.文献[8]设计了一种基于模糊逻辑系统的自适应控制器,该控制器应用函数近似理论对系统不确定性和非线性进行估计,并通过在线改变模糊逻辑系统参数来实现系统的实时控制.文献[9]提出一种基于反演运动学控制器与双自适应神经滑模鲁棒动力学控制的混合鲁棒控制算法,在有效应对系统不确定性的同时,消除了滑模控制中的输入抖振现象,但系统过于复杂,不利于实时控制.文献[10]基于反演技术和自适应滑模控制设计了具有全局渐近稳定特性的轨迹跟踪控制器,但与上述其它鲁棒控制方法相似,都是从AGV参考点输出建立近似动力学模型,而忽略了执行器等的不确定性影响,系统鲁棒性受到一定的限制.
文中从AGV的运动学和动力学模型出发,建立了从执行器输出的AGV严格不确定动力学模型,同时设计了一种具有输入-输出非线性反馈线性化控制和自适应反演滑模控制的AGV轨迹跟踪控制器.非线性反馈控制将AGV的复杂非线性动力学系统反馈线性化,自适应反演滑模控制将自适应控制和基于反演设计方法的滑模控制有机结合,有效克服了AGV未建模部分和外部未知扰动的影响;采用自适应方法估计滑模的鲁棒部分,还有利于削弱抖振现象,且与其它鲁棒控制方法相比,其物理实现更为简单,有利于提高系统的实时性.
1 AGV的模型分析
研究对象为如图1所示的(2,0)型[11]差分驱动三轮式AGV,它由具有两个驱动轮和一个辅助前轮(万向轮)的小车组成,辅助前轮起到支撑车体和导向的作用,同轴的两驱动轮采用独立电机驱动,通过对两驱动轮的不同转速和转向控制可实现AGV的多种运动形式.
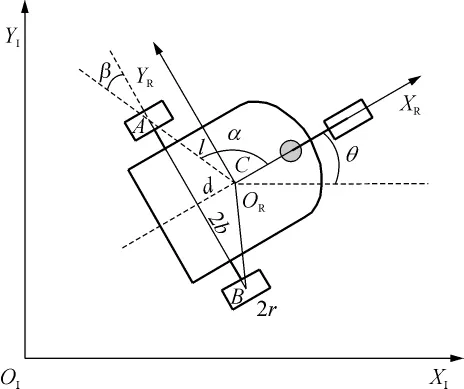
图1 AGV结构示意图Fig.1 Schematic diagram of AGV
AGV惯性坐标系为XIOIYI,局部坐标系为XRORYR,OR位于小车的质心C处,惯性坐标系与局部坐标系X轴的夹角为θ,用向量 ζI=(xC,yC,θ)T表示AGV在惯性坐标系下的位姿.两轮轴线距离为2b,C与两轮轴线的距离为d,AC两点的距离为l,与XR轴的夹角为的夹角为β,两驱动轮A和B的角位移分别为φA和φB,轮子半径为r.
1.1 运动学分析
假设AGV各轮为无变形的刚体,则非完整约束使得AGV仅能沿两驱动轮轴线垂直方向运动,即满足纯滚动和无滑动的条件,则对于固定标准轮A和B有如下约束方程[11]:

式中,R(θ)=为坐标系正交旋转变换矩阵.由图1所示几何关系可知:

令AGV广义位姿为q=[xCyCθφAφB]T,轮速v=[˙φA˙φB]T,则由式(1)、(2)可得AGV的运动学方程为

式中,
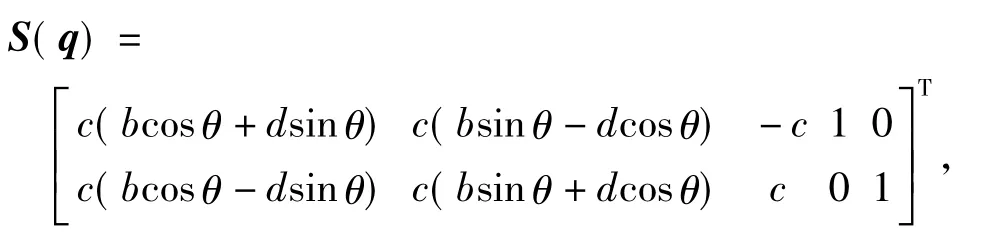
为AGV的广义Jacobian矩阵,它反映AGV关键点速度与驱动轮转速之间的关系,同时也反映AGV关键点作用力与驱动轮驱动力之间的关系,其中c=r/2b.
式(3)表明,仅考虑运动学静态约束,通过对AGV两驱动轮的速度控制即可完全实现对AGV的位姿调整.然而,在实际环境中,AGV动力学动态约束与输出轮速存在复杂的耦合关系,若忽略对其轮子驱动力矩的考虑,往往得不到期望速度,会使轨迹跟踪误差加大,甚至无法实现跟踪.
易验证AGV的广义速度˙q可满足如下非完整约束方程:

式中,A(q)=为AGV约束反力的约束矩阵.由式(3)、(4)可知

即矩阵S(q)为满秩矩阵A(q)零空间的一组基.
1.2 动力学分析
将AGV看作刚体,其在水平面运动,不失一般性,可忽略AGV重力对系统平衡的影响,并忽略辅助前轮阻力矩,则图1所示AGV满足在XI和YI方向的力平衡,以及ZI方向和两驱动电机轴方向的力矩平衡,由此可以得到AGV的动力学约束方程:

式中:mw为轮子质量;m为AGV的整体质量;fxA、fxB为A、B两轮沿XI方向的约束反力;fy为整车YI方向的约束反力;JA、JB分别为A、B两轮驱动电机输出轴的惯量;&A、&B分别为A、B两轮驱动电机的输出力矩;J为整车绕质心轴(ZR轴)的惯量,满足

Jc为车体部分的惯量,Jm为电机部分惯量.
整理式(6)可得到AGV非完整约束下广义力学系统的拉格朗日标准形式:

式中:M(q)∈R5×5,为系统惯性矩阵;E(q)∈R5×2,为系统输入变换矩阵;Vm(q,)∈R5×5,为系统与位置和速度有关的向心力和哥氏力;γ∈R3×1,为系统约束反力向量(拉格朗日乘子);τ∈R2×1,为系统输入向量.
将式(5)和两端求导后的式(4)代入两端乘以ST(q)后的式(8),则可消去系统约束反力项,得到AGV简化后的动力学方程:

式(9)示出了两驱动轮的驱动力矩与AGV关键点的加速度及速度之间的关系,表明AGV为非线性系统,并具有强耦合、多输入、多输出的特性.可见,为实现精确的位置轨迹跟踪,实际应用中应当考虑AGV的动力学约束.
令x=[qTvT]T,并以U为新的辅助输入量,考虑如下非线性反馈控制律:

式中,“+”表示广义逆,H=(STMS)-1SE,f1=(STMS)-1ST(-M˙Sv-Vm).将式(10)代入方程(9),并结合式(3),则可得到简化的有约束力的“二阶运动学模型”:

式中,g1(x)=
可见,在理想状态下,假设AGV无外部干扰,利用目标轨迹Gd得出轮子参考加速度,并令

则AGV进行“完美速度跟踪”,即可完全实现对目标轨迹的跟踪任务.然而,实际系统中的物理参数估计不完全正确,模型具有不确定性,不可避免地存在外部干扰;考虑到这些因素,就需要设计伺服补偿器来降低这些不利影响.为此,文中采用自适应反演滑模控制器作为AGV的伺服补偿器.
2 AGV轨迹跟踪控制器的设计
2.1 控制器结构
文中提出的AGV轨迹跟踪控制器的结构如图2所示,该控制器由非线性反馈控制器(虚框1)和基于自适应反演滑模控制的伺服补偿器(虚框2)组成,虚框3所示部分实现速度输入的反馈线性化,P为相应的满秩解耦矩阵,定义输出反馈向量为N,则有


图2 AGV轨迹跟踪控制器的结构Fig.2 Structure of trajectory tracking controller for AGV
考虑系统模型的不确定性,则


式中,F∈R2×1,为系统有界总体不确定性,包括不确定的AGV模型误差和外部干扰,其表达式为

由图2所示控制器结构可知

则以u为新的辅助输入向量,结合式(16)可得如下状态方程:

式中:P∈R2×2,为S(q)前两行组成的矩阵;Y∈R7×1,为系统的输出向量.
2.2 自适应反演滑模控制算法
为实现AGV的轨迹跟踪控制,伺服补偿器的控制算法是关键.常规PD控制器结构简单,但在应对系统非线性、时变或不确定性时,适应性差;滑模控制采用不连续且结构不固定的动态控制策略,通过控制量的切换使系统状态沿着滑模面(切换面)滑动,从而使系统在受到参数摄动和外部干扰时具有不变性及很好的鲁棒性,适用于各类控制系统.然而,滑模控制在应对难以精确估计的无上界的总体不确定性时,易造成影响系统应用性能的高频抖振.采用自适应的方式实现对其总体不确定性F的估计[12],可以有效地削弱抖振现象,同时使控制器具备自适应和自学习特性,从而进一步提高控制器的性能.
反演设计方法将复杂的非线性系统分解成不超过系统阶数的子系统,然后与普适性强的李雅普诺夫(Lyapunov)直接法结合完成整个控制律的设计.该方法综合考虑了控制律和自适应律,使得闭环系统满足期望的动静态性能.文中提出的基于自适应反演滑模控制的AGV伺服补偿器分两个步骤进行设计.
步骤1:
令AGV轨迹跟踪位置误差向量为

其中qa=[xCyC]T,定义系统稳定项

式中,c∈R2×2,为对称的正定常数矩阵.
选择如下正定的Lyapunov函数:

定义中间虚拟控制量为

则有

显然,上式中若z=0,则为误差向量e的二次型函数,即≤0,需进行第2步的反演设计.
步骤2:
定义正定Lyapunov函数为

式中,σ为切换函数,FE为总体不确定性F上界的估计误差,μ为正的常数.
定义切换函数为

式中,k∈R2×2,为对称的正定常数矩阵.
定义F的估计误差为

式中,F*和分别为F的真值和估计值.
将式(22)、(24)、(25)、(27)代入求导后的式(26),有

对式(21)二次求导,同时结合式(20)、(28)有

将式(30)代入式(29)可得

取AGV自适应反演滑模轨迹跟踪伺服补偿器的输出为

式中,h、λ∈R2×2,为对称的正定常数矩阵.设计自适应律为

将式(32)、(33)代入式(31)得

式中,λii为λ的元素,σi为 σ 的元素.
取
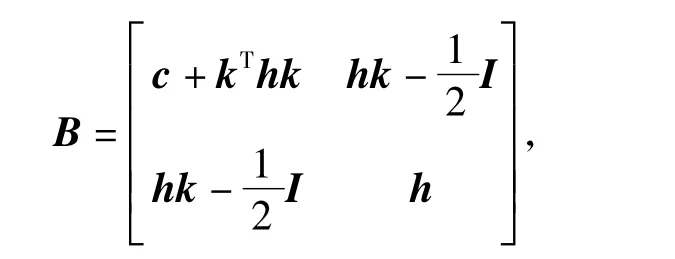
则有
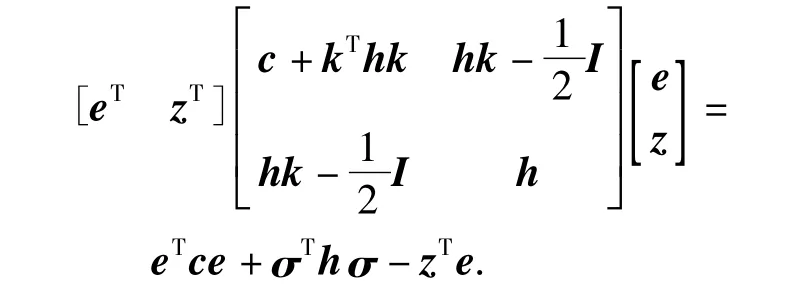
通过取适当的c、k的数值,可使>0,即可使得B为对称正定矩阵,令s=[ez]T,此时有

如果定义如下项:

则有

因为V2(s(0))有界,V2(s(t))有界且非增,则有Barbalat引理可得即当时间t→∞时,位置偏差e和中间控制量z都将趋近于零.可见,通过上述自适应反演滑模伺服补偿器的设计,整个控制系统是收敛且渐近稳定的,保证了AGV按期望轨迹进行运动.

由于(t)也是有界的,则W(t)是一致连续的,根据
3 仿真实验
为验证文中轨迹跟踪控制器的控制效果,在Matlab环境下对系统进行仿真.AGV仿真模型的物理参数如下:b=0.60 m,d=0.12 m,r=0.06 m,m=200.0kg,mc=181.0kg,mw=3.0kg,Jc=35.625kg·m2,JA=JB=35.625kg·m2,Jm=0.06kg·m2.系统外部随机干扰设为
τd=[random( -10.0,10.0) random( -10.0,10.0)]T.
系统的模型不确定性设为
Δf1=[3.6sint3.6sint]T,
ΔH=diag(costcost).
期望运动轨迹为一椭圆,其参数方程为

自适应反演滑模伺服补偿器的参数如下:c=diag(5.0 5.0),k=diag(14.0 14.0),h=diag(18.0 18.0),λ=diag(1.0 1.0),μ=4.0.AGV的初始位姿为:xC=8.0m,yC=5.0m,θ=π.
在AGV具确定性模型和不确定性模型时,分别采用自适应反演滑模控制(ABSMC)、基于指数趋近律的滑模控制(ESMC)和PD控制3种方案进行椭圆轨迹跟踪.在AGV具确定性模型时的实验结果如图3(a)所示.由图可见,3种方案都能完成轨迹跟踪任务,而文中设计的控制器的控制效果明显优于另外两种控制器.在AGV具不确定性模型时的实验结果如图3(b)所示.由图可见,ESMC和PD控制均未能有效地进行轨迹跟踪,而文中提出的控制器ABSMC仍然有效,消除了模型不确定性和外部干扰对系统的影响.图4所示的实验结果表明,不确定模型下,文中提出的控制器可以在不同起始位姿对参考轨迹进行跟踪.图5和图6(a)、6(b)分别给出了起始位姿为(8.0,2.0,π)时X、Y轴的跟踪误差和左右轮的控制力矩输出,结果表明,所提出的控制器响应速度快,跟踪精度高,力矩输出平稳,有效地削弱滑了模控制引起的抖振现象.

图3 具确定性模型与不确定模型时的AGV轨迹跟踪Fig.3 Trajectory tracking of AGV with deterministic and uncertain models

图4 采用文中提出的控制器时不同初始位姿的轨迹跟踪Fig.4 Trajectory tracking of different start poses by using the propsed controller

图5 采用文中提出的控制器时X轴和Y轴的跟踪误差Fig.5 Trajectory errors of X and Y axes obtained by the propsed controller
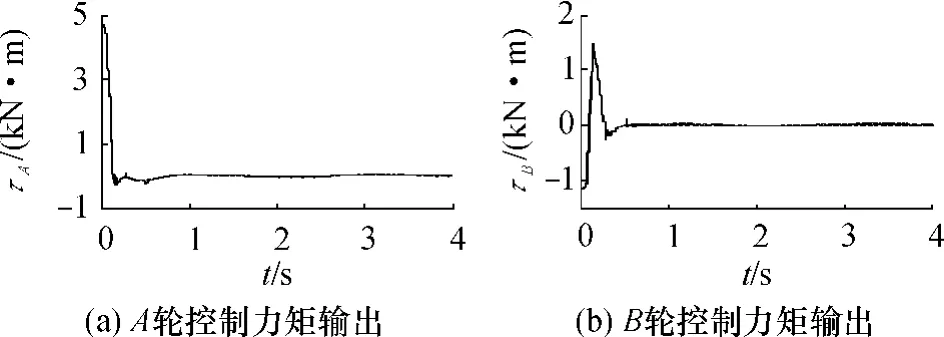
图6 采用文中提出的控制器时A轮与B轮的控制力矩输出Fig.6 Control torques of wheels A and B obtained by using the propsed controller
4 结语
针对动力学系统下具有模型不确定性和外部未知干扰的非完整AGV的轨迹跟踪问题,建立了从执行器输出的AGV严格不确定动力学模型,设计了一种具有输入-输出非线性反馈线性化控制和位置伺服补偿的轨迹跟踪控制器.该控制器对AGV复杂非线性动力学系统进行反馈线性化,并应用基于反演设计方法的自适应反演滑模控制方法对AGV不确定模型和外部扰动进行伺服补偿,保证AGV快速而精确地跟踪期望轨迹,仿真结果证明了该控制器的有效性.下一步将在实际AGV系统上进行实验研究.
[1]Flickinger D M,Minor M A.Remote low frequency state feedback kinematic motion control for mobile robot trajectory tracking[C]∥Proceedings of the 2007 IEEE International Conference on Robotics and Automation.Roma:IEEE,2007:3502-3507.
[2]Ye Jun.Tracking control for nonholonomic mobile robots:integrating the analog neural network into the backstepping technique [J].Neurocomputing,2008,71(16/17/18):3373-3378.
[3]Chwa Dongkyoung.Sliding-mode tracking control of nonholonomic wheeled mobile robots in polar coordinates[J].IEEE Transactions on Control Systems Technology,2004,12(4):637-644.
[4]吴忻生,任华瑛.非完整移动机器人轨迹跟踪的最优模糊控制[J].华南理工大学学报:自然科学版,2004,32(3):44-49.Wu Xin-sheng,Ren Hua-ying.An optimized fuzzy control approach to the trajectory tracking of nonholonomic mobile robots[J].Journal of South China University of Technology:Natural Science Edition,2004,32(3):44-49.
[5]Ashoorirad M,Barzamini R,Afshar A,et al.Model reference adaptive path following for wheeled mobile robots[C]∥Proceedings of the 2006 IEEE International Conference on Information and Automation.Colombo:IEEE,2006:289-294.
[6]Argenti M,Consolini L,Lini G,et al.Recursive convex replanning for the trajectory tracking of wheeled mobile robots[C]∥Proceedings of the 2010 IEEE International Conference on Robotics and Automation.Anchorage:IEEE,2010:4916-4921.
[7]Kwak Hwan-Joo,Park Gwi-Tae.Design of adaptive PD controller for weight independent target tracking of home service mobile robot[C]∥Pro-ceedings of the 2011 IEEE International Conference on Consumer Electronics.Berlin:IEEE,2011:779-780.
[8]Dax T,Kar I N.Design and implementation of an adaptive fuzzy logic-based controller for wheeled mobile robots[J].IEEE Transactions on Control Systems Technology,2006,14(3):501-510.
[9]王宗义,李艳东,朱玲.非完整移动机器人的双自适应神经滑模控制[J].机械工程学报,2010,46(23):16-21.Wang Zong-yi,Li Yan-dong,Zhu Ling.Dual adaptive neural sliding mode control of nonholonomic mobile robot[J].Journal of Mechanical Engineering,2010,46(23):16-21.
[10]闫茂德,吴青云,贺昱曜.非完整移动机器人的自适应滑模轨迹跟踪控制[J].系统仿真学报,2007,19(3):579-584.Yan Mao-de,Wu Qing-yun,He Yu-yao.Adaptive sliding mode tracking control of nonholonomic mobile robot[J].Journal of System Simulation,2007,19(3):579-584.
[11]Campion G,Bastin G,D'Andréa-Novel B.Structural properties and classification of kinematic and dynamic models of wheeled mobile robots[J].IEEE Transactions on Robots and Automation,1996,12(1):47-62.
[12]Lin F J,Shen P H,Hsu S P.Adaptive backstepping sliding mode control for linear induction motor drive[J].IEE Proceedings Electric Power Applications,2002,149(3):184-194.
