国债期限溢价与股权溢价之间动态相关性分析
2011-08-01王志强熊海芳
王志强,熊海芳
(东北财经大学 应用金融研究中心,辽宁 大连 116025)*
一、引 言
股权溢价是指股票收益高于无风险利率的部分,股权溢价一直是金融市场中受关注的问题。理论上,不同期限国债的收益率反映市场对不同期限利率的预期,国债利率的期限结构会受到宏观经济变量的影响,而其中一些宏观经济变量同样会影响股票收益率,如货币政策、通货膨胀等,因此股权溢价与利率期限结构中的期限溢价之间就存在一定的相关性。本文将采用多元GARCH模型对中国的国债期限溢价和股权溢价之间的动态相关性进行分析。多元GARCH模型(MGARCH)在不同资产之间条件相关性和条件方差的分析中已经得到广泛应用,如 Engle和 Kroner(1995)[1]的 BEKK 模型和Engle(2002)[2]的动态条件相关性模型(Dynamic Conditional Correlation,DCC)。为了考虑方差、协方差和相关性的非对称性,Cappiello,Engle和Sheppard(2006)[3]提出了非对称的动态条件相关性模型 (Asymmetric Dynamic Conditional Correlation,ADCC),他们利用ADCC模型对全球股市和债市收益率进行了分析,结果发现全球普遍存在股票收益的非对称性而债券却很少有这种现象,但是股票和债券都存在非对称的条件相关性。袁超等(2008)[4]运用 ADCC对中国股市和债市的相关系数的时变性进行研究,结果发现两个市场的相关性存在结构性变化。王璐和庞皓(2009)[5]则使用BEKK模型对股市和债市的波动溢出进行研究。
中国的国债市场自从1996年以来得到不断发展,国债市场与股票市场有着紧密的联系,两个市场的关系也是不断变化的[4],但已有研究对利率期限结构的期限溢价与股权溢价之间的动态关系关注却较少。与王璐和庞皓(2009)使用BEKK-MGARCH模型、袁超等(2008)使用ADCC-MGARCH模型分析股票指数和债券指数之间关系不同的是,本文分析期限溢价和股权溢价的关系,采用窗口滚动、BEKK-MGARCH和 ADCC-MGARCH 三种方法进行比较,检验不同动态相关系数的效果差异。同时,本文使用2002年1月~2010年3月的月度数据进行分析,不仅避免了日交易数据高度波动的影响,而且包含了2008~2009年经济危机时期。此外,本文不仅考虑期限溢价和股权溢价之间的动态相关性的时变性,而且关注其符号的变化。
二、实证分析
本文的数据来源于锐思金融数据库,数据区间为2002年1月~2010年3月。证券市场指数采用上证综指,上证综指的月度收益率使用ret表示。同时考虑交易所债券市场在2009年后的交易比较少,国债数据使用银行间债券市场数据。为了得到不同期限的无风险利率,考虑 Nelson-Siegel(1987)[6]简约利率期限结构模型的灵活性和广泛使用[7],本文根据 Diebold和 Li(2006)[8]扩展的 Nelson-Siegel模型估计即期利率,得到1年和10年的无风险即期利率y1和y10,其中期限溢价sp101,等于10年期利率减去1年期利率。股票指数收益率与1年期即期利率的差为股权溢价exret。
为了得到国债期限溢价和股权溢价的动态相关性并进行比较,本文首先采用简单的窗口滚动来计算动态相关性,然后采用两个多元GARCH模型进行分析,进而分析动态条件相关系数的变化。
(一)窗口滚动样本相关性
由于本文采用的是月度数据,所以首先采用前6期的数据来计算初始的相关性系数,然后逐月向后滚动得到每个月的滚动相关性系数corrl,其计算公式如下:
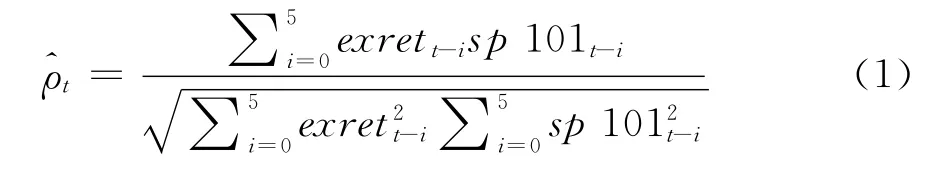
根据公式(1)计算的样本相关性序列corrl的时间序列图见图1。图中结果显示,期限溢价和股权溢价之间的相关性系数呈现正负交替的波动性。
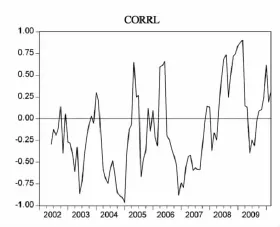
图1 窗口滚动样本相关性
(二)BEKK-MGARCH 模型
为了进行比较,同时考虑金融时间序列的非对称性,本文分别采用BEKK-MGARCH模型和考虑非对称性的ADCC-MGARCH模型来分析exret和sp101之间的动态相关性。
根据BEKK-MGARCH模型,本文首先设定exret和sp101的一阶自回归方程,形式为:

exret和sp101的方差和协方差的方程则为:
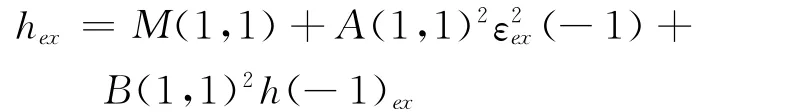

估计动态条件相关系数的公式为:
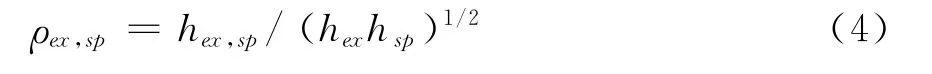

表1 BEKK-MGARCH模型的估计结果
从表1中可看出,exret的均值方程系数都不显著,而sp101的均值方程的系数都具有统计显著性。在条件方差和协方差系数中,A(1,1)、A(2,2)、B(1,1)、B(2,2)都是显著的。另外,为了分析条件协方差的变化,分别对其系数 A(1,1)×A(2,2)、B(1,1)×B(2,2)进行 wald检验,发现它们都是显著不为零的,这说明它们的条件协方差短期具有ARCH效应,长期具有GARCH效应。为了分析exret和sp101之间相关性的时变性,图2画出BEKK-MGARCH模型中的条件相关系数走势。
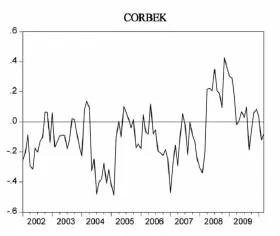
图2 exret和sp101之间的条件相关系数:BEKK-MGARCH模型
从图2中看出,基于BEKK-MGARCH模型的exret和sp101之间的条件相关系数,其走势呈现上下波动,说明它们之间存在动态的相关性。
(三)ADCC-MGARCH 模型
为了更全面地分析exret和sp101之间的相关性的时变性,下面采用ADCC-MGARCH模型进行分析:

其中,ri,t是资产收益溢价i在t期的数值,σi,t是资产收益溢价i在t期的条件波动率,σij,t是i和j在时间t的条件协方差,zi,t=ri,t/σi,t,¯σij是无条件协方差,I是指示函数,当εi,t-1大于零时为1,它表示波动的非对称性。得到ADCC-MGARCH模型的估计结果如表2。

表2 ADCC-MGARCH模型的估计结果
从表2可看出,除sp101的非对称性系数不显著外,其他各个系数基本都具有高度的显著性,δ(ex)显著表明波动存在非对称性,α、β均显著不为零,说明滞后一期的标准化残差乘积对动态相关系数存在影响,α+β接近于0.9,反映出相关性具有较强的持续性特征。为了更好的比较分析exret和sp101之间相关性的时变性,画出ADCC–MGARCH模型中的条件相关系数的走势,如图3。

图3 exret和sp101之间的条件相关系数:ADCC-MGARCH模型
从图3可以看出,基于ADCC-MGARCH模型得到的exret和sp101之间的条件相关系数也是时变的,可以看出:2002~2007年国债期限溢价和股权溢价的相关性基本为负数,其中,2002~2003年相对平稳,2004~2005有下降的趋势,2006~2007年在波动中上升,2008~2009两者相关性是正数。其中,2008年不断上升,2009年以来呈现不断下降趋势。从图2、图3可以看出BEKK-MGARCH模型与ADCC-MGARCH模型估计的时变相关系数的差别很大,前者估计的相关系数波动经常发生转折,而后者的情形则相对稳定。
(四)三个动态相关系数的比较
对于国债期限溢价和股权溢价的动态相关性,本文得到3个结果:窗口滚动相关性系数corrl、BEKK模型的条件相关系数corbek和ADCC模型的条件相关系数cordcc。为了判断哪个模型能更好的反映股权溢价和国债期限溢价之间真实相关系数的时变性,本文对它们进行统计分析,比较哪个更符合实际。表3是这3个变量的统计特征。
在表3中,corrl、corbek和cordcc的均值都为负数,cordcc的均值与样本数据静态相关系数-0.10685最为接近,说明ADCC的效果较好。另外,窗口滚动的相关系数corrl最大值、最小值比较接近于1与-1,cordcc次之,corbek的绝对数相对都较小;3个相关系数都呈现左偏,说明模型中的相关系数多数为负数。实际上,前些年中国的国债市场和股票市场之间的相关性并不是很强,而2008年金融危机以来股市震荡、债市回暖时期股价下跌、债券价格上涨,2009年期限溢价和股权溢价的相关性应该是下降的,3个相关系数中ADCC刚好与这些现实情况相符合。从图3可以看出,股权溢价和国债期限溢价条件相关系数大小在短期内就会发生变动,具有时变性,但两者的相关系数在2007年前多为负数,2008~2009多为正数,说明股权溢价和国债期限溢价的相关性在短期内不断发生变动,但是在正负相关性上却保持相对稳定。

表3 动态条件相关性系数统计特征
三、结 语
为了得到国债期限溢价和股权溢价的动态相关性,本文采用窗口滚动、BEKK-MGARCH和ADCC-MGARCH模型,分析两者动态条件相关系数的变化及差异。对于国债期限溢价和股权溢价的动态相关性,本文结果发现ADCC-MGARCH模型的条件相关系数cordcc的均值与样本数据静态相关系数最为接近,同时,3个相关系数中ADCC也与现实情况最为相符。从ADCC-MGARCH的条件相关系数看,发现股权溢价和国债期限溢价条件相关系数大小在短期内就会发生变动,但与他们发现相关性的正负符号在短期就会变化不同,中国市场中两者的相关性在正负符号上却保持相对稳定。
[1]Engle R F,Kroner K F.Multivariate simultaneous generalized ARCH [J].Econometric Theory,1995,11(1):22-150.
[2]Engle R F.Dynamic conditional correlation - a simple class of multivariate GARCH models[J].Journal of Business and Economic Statistics,2002,20(3):339-350.
[3]Cappiello L,Engle R,Sheppard K.Asymmetric dynamics in the correlations of global equity and bond returns[J].Journal of Financial Econometrics,2006,4(4):537-572.
[4]袁超,张兵,汪慧建.债券市场和股票市场的动态相关性研究[J].金融研究,2008,(1):63-75.
[5]王璐,庞皓.中国股市和债市波动溢出效应的MV-GARCH分析[J].数理统计与管理,2009,(1):152-158.
[6]Nelson C R,Siegel A F.Parsimonious modeling of yield curves[J].Journal of Business,1987,60(4):473-89.
[7]康书隆,王志强.中国国债利率期限结构的风险特征及其内含信息研究[J].世界经济,2010,(7):121-143.
[8]Diebold F X,Li C.Forecasting the term structure of government bond yields[J].Journal of Econometrics,2006,130(2):337-364.
[9]刘懿,罗希.我国次级债券市场约束的实证研究[J].科学决策,2009,(10):26-34.
