基于属性相关分析的离群数据并行挖掘算法

2011-08-01张继福

太原科技大学学报 2011年5期

王磊,张继福

(太原科技大学计算机科学与技术学院,太原030024)

离群数据(Outlier)就是明显偏离其他数据,不满足数据的一般模式或行为,与存在的其他数据不一致的数据[1]。离群数据挖掘问题可以看作两个子问题:(1)定义在给定的数据集合中什么样的数据认为是不一致的;(2)找到一个有效的方法挖掘这样的离群数据。离群数据挖掘作为数据挖掘的一种重要技术,在欺诈检测、网络安全分析、入侵检测等领域有广泛的应用[2]。

目前,国内外主要的离群数据挖掘算法大致可分为基于统计的方法[1]、基于距离的方法[3]、基于深度的方法[4]、基于密度的方法[5]和基于偏差的方法[6]等。随着数据规模的不断增大,高维海量离群挖掘是当前研究热点之一,其主要研究成果有:Aggarwal和Yu[7]于2005年提出的投影离群数据检测算法,Cui Zhu[8]等提出的基于用户实例的高维数据检测算法,张继福[9-10]等通过引入稠密度系数提出的基于概念格的离群数据挖掘算法,葛凌云[11]等提出的利用微粒群算法搜索稀疏子空间算法,Mohamed[12]等提出的基于属性相关分析的聚类算法。蔡江辉[13]等提出了一种基于聚类的离群挖掘算法。但是,这些方法都是在单机环境下运行的,随着信息技术的不断发展,大量的数据被存储在数据库中,且数据普遍具有分布稀疏、维度高、数据量呈指数增长等特点,这些因素都对计算机的单机计算能力提出了非常高的要求。与此同时,受限于大型机、巨型机的昂贵价格,使它们在实际应用中几乎不可能得到普及,并行离群挖掘算法成为解决这一问题的有效途径,即将许多运算能力相对低下计算机构成计算机组,通过并行计算的方式,以相对低廉的价格获得强大的运算能力,从而在普通的实验环境中实现高维海量数据的离群挖掘工作。目前,并行离群挖掘的研究成果还比较少,王玮[14]等针对海量数据提出了一种基于网格的概念格分布式构造算法,对本文的并行算法具有一定的借鉴意义。

针对上述问题,本文提出了一种基于属性相关分析的并行局部离群数据挖掘算法。该算法在并行计算环境中,首先由主节点分配属性相关分析任务,各个子节点分别读取数据子集并计算各数据子集的冗余属性,通过数据通信传送回主节点后由主节点将冗余属性删除,从而有效的实现数据集的降维目的;其次由主节点分配搜索任务,各个子节点读取数据子集后根据用户设定的稀疏度系数阈值,采用微粒群算法搜索各数据子集的稀疏子空间,由主节点进行合并计算后,确定最终的局部离群数据;最后,采用天体光谱数据作为数据集,实验结果验证了该算法的正确性和有效性,从而为海量高维离群数据挖掘提供了一种新途径。

1 基本概念

1.1 基于属性相关分析的局部离群数据挖掘算法

基于属性相关分析的高维离群数据挖掘的基本思想可归纳为[15]:首先利用属性相关分析,删除冗余属性;然后使用微粒群算法,根据用户确定的稀疏度系数阈值搜索稀疏子空间;最后根据稀疏子空间确定局部离群数据。其中,属性相关分析通过检测每个属性维的稠密和稀疏区域分布搜索冗余属性。有关定义描述如下:

定义1 对于任意一个d维数据集,属性集A={A1,A2,…Ad},数据对象集 X ={X1,X2,…Xn},Xij(i=1,2,…n;j=1,2,…d)表示第i个数据对象在第j个属性上的相关值,称Xij是一个1-d点。

为了检测每一属性上的区域分布,需要计算每一个1-d点Xij的稀疏因子。

定义2 Xij的稀疏因子定义为:对象在各维中是否处于稠密区域。

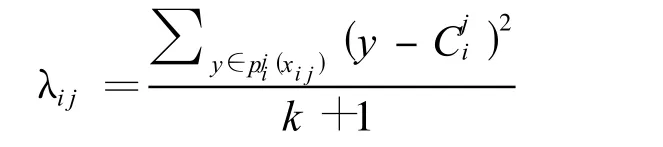
定义4 对于任意数据集,对象集为N,属性集为 D,存在属性Aj,如果(利用定义2和3),即属性Aj是由稠密区域构成的维,则称它是冗余属性。

根据定义4可以删除数据集中的冗余属性。在缩减后的数据集中,为了度量子空间内数据的偏离程度,采用文献[7]定义的稀疏度系数作为子空间偏移程度的度量因子。

定义5 稀疏度系数S(D)的表达式定义为:

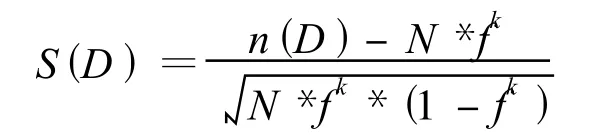
其中,n(D)是包含在D中的对象数,f=1/Φ.对于局部离群数据,它所在的子空间内包含的数据条数远低于平均值,因此稀疏度系数S(D)小于0.

定义6 根据定义5计算子空间S的稀疏度系数,TS为用户设定的稀疏度阈值,若稀疏度系数S(D)＜TS,则称S为稀疏子空间。

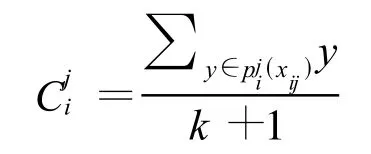
容易发现,λij很大说明1-d点 Xij代表的数据对象i在j属性维上处于稀疏区域,反之则说明其处于稠密区域。为了识别稠密区域,这里设置一个阈值 ε来判断。

定义3 如果 Xij的稀疏因子 λij＜ε,则令 Zij=1,并称Xij属于稠密区域,反之,则令 Zij=0,并称 Xij属于稀疏区域。

根据定义3,可以列出一个稀疏度密度矩阵Z(n*d),通过矩阵Z,可以很清晰的看出每个数据可知,它的维数均不大于logθ(N/TS2+1)。

假设D维属性集中包含N个数据对象,缩减后的属性集维数为A.选取k维作为子空间,且将k维作为A维空间的微粒,稀疏度系数作为适应值函数,利用微粒群算法可以找出稀疏子空间并确定局部离群数据。

1.2 并行计算与MPI

并行计算或者并行处理,指的是利用多个具有计算能力的部件来共同完成一个计算工作,获得比用一个部件来完成要快的效果,它是计算数学与新一代计算机相结合的产物[16]。并行计算以其强大的计算能力、优越的性价比、成熟的技术和设备、良好的可移植性和可伸缩性成为大规模数据分析的有效支持工具。目前,最流行的两个并行计算支持环境是PVM和 MPI。MPI(Message Passing Interface)[17]是一种消息传递标准或规范,它以可移植性强、模块性高、应用领域灵活而受到国际上的广泛重视。

并行计算中的数据集划分方式主要分为两类:水平划分和垂直划分。假设DB是由D维属性、N条数据构成的数据集,可以将DB水平或者垂直的划分成m个子集。水平划分即DB=DB1∪DB2…∪DBm,且DBi∩DBj=Ø(1≤i≤m,1≤j≤m),|DB1|+|DB2|+… +|DBm|=N.垂直划分即DB=DB1∪DB2…∪DBm,且attr(DBi)∩attr(DBj)=Ø,|attr(DB1)|+|attr(DB2)|+… +|attr(DBm)|=D,attr(DBi)表示数据集DBi的属性子集(1≤i≤m,1≤j≤m)。

2 基于属性相关分析的并行离群挖掘方法

针对大规模高维数据集,其庞大的数据存储、复杂的数据结构都使单机环境下的数据挖掘算法变的越来越复杂。虽然近期国内外学者提出了一些针对高维海量数据的算法,但面对数据量的指数级增长和硬件环境的制约,这些算法也面临各种各样的使用限制甚至瓶颈。针对上述问题,采用并行计算的思想,对基于属性相关分析的高维离群数据挖掘算法进行改进,使其在普通的实验环境下也能获得较高的效率。该算法主要由两部分构成:属性相关分析删除冗余属性和微粒群算法搜索离群子空间。

属性相关分析是依据每维的稀疏稠密性删除冗余属性的,而各维的稀疏稠密性可以根据定义2、3、4按属性维独立运算,各维之间互不影响,因此属性相关分析可以用垂直划分的并行计算来实现。在属性相关分析删除冗余属性过程中,主节点首先根据子节点数M和属性数D垂直划分(D/M)数据集P.主节点分配任务后,子节点利用属性相关分析求出每个数据子集的冗余属性。然后子节点将冗余属性序号传回主节点,由主节点合并处理后删除冗余属性,此时数据集为缩减属性的数据集,记为缩减集Q.

采用微粒群算法搜索离群子空间是通过判断随机子空间的稀疏程度确定的,根据微粒群算法的特点,子空间的随机选择过程又通过随机选定属性实现,因此微粒群搜索离群子空间可以采用水平划分的并行计算来实现。采用水平划分的方法可以保证各数据子集中属性的完整性,进而也保证了离群子空间搜索结果的完备性。在微粒群算法搜索离群子空间过程中,主节点根据子节点数M和数据条数N水平划分(N/M)缩减数据集Q.主节点分配任务后,子节点根据用户设定的稀疏度阈值,使用微粒群算法在各自分配的数据子集上搜索局部稀疏子空间。然后将局部稀疏子空间的相关信息(包括数据条数,数据记录号,属性序号)传回主节点,主节点通过对相同局部稀疏子空间的数据条数进行合并,生成全局子空间。最后,主节点根据稀疏度阈值对全局子空间进行判断,识别出全局稀疏子空间和离群数据。

定理1 对于任意一个D维属性、N条数据构成的数据集,任意由冗余属性构成的子空间都不是稀疏子空间。

证明假设子空间Q是由冗余属性构成的稀疏子空间。据定义5⇒子空间Q的稀疏度系数S(D)＜TS,再由定义4⇒冗余属性即由稠密区域构成的属性,而冗余属性的稠密性远大于非冗余属性的稠密性 ⇒稀疏子空间Q的稠密性远大于其他子空间的稠密性,即其他子空间的稀疏度系数S(D)′＜TS,据定义6⇒其他子空间也是稀疏子空间数据集中所有的子空间都是稀疏子空间。与假设矛盾,定理1得证。

定理2 在属性相关分析中,并行计算环境和单机环境删除冗余属性的操作结果一致。

推论1 在并行实验环境下,删除冗余属性对离群数据挖掘的精度没有影响。

证明由定理1可知,删除冗余属性对搜索稀疏子空间的结果没有影响,即对离群挖掘的精度没有影响,由定理2可知,并行环境和单机环境下的属性相关分析结果一致,所以,并行实验环境下,删除冗余属性不影响离群挖掘算法结果。

定义7 假设DB是由D维属性、N条数据构成的数据集。数据集水平划分后,如果各个子节点分析的数据子集中,存在稀疏度系数小于用户设定的系数度阈值的子空间(利用定义5和6),即S(D)＜TS,则称这些子空间为局部稀疏子空间。

定义8 假设DB是由D维属性、N条数据构成的数据集。数据集水平划分后,如果各子节点分析的数据子集中,存在属性序号相同,数据记录号不同的子空间,则称这些子空间为相同局部子空间。如果这些子空间同时满足定义7,则称它们为相同局部稀疏子空间。

定义9 在相同局部稀疏子空间中,如果数据对象合并后,仍然满足定义5和6,即S(D)＜TS,则称合并后的子空间为全局稀疏子空间,全局稀疏子空间中所包含的数据对象称为局部离群数据。

定理3 如果各个子节点的相同局部子空间中存在非局部稀疏子空间,那么这些相同局部子空间合并后的全局子空间必定不是全局稀疏子空间。

证明设子节点I上存在一个非局部稀疏子空间P,P的相同局部子空间都是局部稀疏子空间,由定义6可知,P不满足S(D)＜TS,由于稀疏度系数TS不变,易知数据条数合并后的全局子空间必定也不满足S(D)＜TS,即这个全局子空间不是全局稀疏子空间。

推论2 并行环境下搜索的全局稀疏子空间与单机环境的稀疏子空间一致。

证明由于微粒群算法的适应值函数一致,由定义9和定理3可知,数据对象的个体和全局最优位置一样,即稀疏度系数也一致。所以,并行环境下的全局稀疏子空间和单机环境的稀疏子空间也一致。

推论3 基于属性相关分析的并行局部离群挖掘与单机环境的结果一致。

证明本文并行算法由两部分构成。由推论1和推论2可知,属性相关分析和微粒群搜索算法的并行与单机结果都一致,易知基于属性相关分析的并行局部离群挖掘算法和单机环境下的算法结果一致。

3 算法描述

根据上述描述的基本思想,基于属性相关分析的并行局部离群数据挖掘算法由两个子算法构成:并行属性相关分析算法和并行微粒群搜索算法。

算法1 并行属性相关分析算法

输入:原始数据集DB,稀疏因子阈值 ε,子节点数目M

输出:缩减数据集RDB

(1)主节点根据子节点数目M和数据集维数D,由D/M划分各个子节点要计算的数据子集(此次划分为垂直划分);

(2)主节点通过第一次网络通信分配属性相关分析任务,子节点1的任务为属性(1,D/M)的数据子集,依次类推,子节点I的任务为属性((M-1)D/M+1,ID/M)的数据子集;

(3)各个子节点通过用户设定的稀疏因子阈值ε,使用属性相关分析对各自的数据子集进行运算,找出各数据子集的冗余属性;

(4)各子节点通过第二次网络通信将冗余属性序号传回主节点;

(5)主节点对数据子集的冗余属性进行汇总,得出原始数据集DB的冗余属性;

(6)主节点对原始数据集的冗余属性进行删除,得出缩减数据集RDB.

算法2 离群数据并行挖掘算法

输入:缩减数据集RDB,稀疏度系数阈值S,子节点数目M

输出:局部离群数据

(1)主节点根据子节点数目M和缩减数据集条数N,由N/M划分各个子节点要计算的数据子集(此次划分为水平划分);

(2)主节点通过第三次网络通信分配微粒群搜索任务,子节点1的任务为数据编号(1,N/M)的数据子集,依次类推,子节点I的任务为数据编号((M-1)N/M+1,IN/M)的数据子集;

(3)各个子节点通过稀疏度系数S,使用微粒群算法搜索各数据子集,找出局部稀疏子空间;

(4)各子节点通过第四次网络通信将局部稀疏子空间的相关信息(包括数据条数,数据记录号,属性序号)传回主节点;

(5)主节点对相同局部稀疏子空间的数据条数进行合并,得出全局子空间的集合;

(6)主节点通过稀疏度系数,对全局子空间进行判别,得出全局稀疏子空间;

(7)主节点根据数据记录号得出最后的离群数据。

在算法1和2中,共进行了4次网络通信,两次任务分配通信和两次结果回传通信。由于网络通信仅传输属性序号、数据标号等信息,并不涉及具体数据的通信,其数据量传递较少,因此,局域网网络通信代价几乎可以忽略。在算法1中,由于attr(DBi)∩attr(DBj)=Ø,各子节点可以独立进行属性相关分析,步骤3的理论运行效率接近T/M(T是单机环境下运行属性相关分析的时间,M是子节点个数),而其他步骤中的通信和数据库读写时间相对较小,算法1能较好的提高效率。微粒群算法不是线性算法,随着数据量的增大,其运行时间也会大幅增加,而算法2由各子节点独立的搜索离群子空间,其步骤3的理论运行时间小于T/M(T是单机环境下运行微粒群搜索的时间,M是子节点个数),同样算法2的通信和合并计算时间代价相对较小,算法2也能大幅缩短运行时间。

4 实验结果分析

采用国家天文台提供的高红移类星体、晚型星、类星体、恒星四个SDSS天体光谱数据,经过离散化以后作为实验数据集[18],其中:44条光谱特征线作为属性,即:维数 =44、光谱数据集分别含有5403(7M)、34117(46M)、71601(99M)、74614(104M)条,数据库为E5506CPU,8GB内存做服务器的ORACLE 9i数据库。实验设备使用4台Pentium D925 CPU,512 MB内存计算机作为子节点,其中1台同时作为主节点。实验平台为MPICH2-1.0.3的并行环境,采用Visual C++6.0实现了本文所提的单机算法和并行算法。

在实验中,稀疏度系数取-1,稀疏因子取0.1,微粒群的规模设为N=30,参数c1、c2设为0.5,w为0.8,算法的试验次数为10次,取平均值作为结果。加速比S是衡量并行算法的主要指标,其定义为S=T/P,其中:T表示单机环境的串行耗时,P表示并行运算的耗时,实验结果见图1和图2。

由图1可以看出,在实验环境相同的情况下,并行环境的算法和单机环境的算法找出的离群数据基本相同。说明并行环境下算法的精度与单机环境下算法的精度一致,在上述两个子算法中,并行属性相关分析和单机属性相关分析、并行子空间搜索和单机子空间搜索的结果大体是一致的,从而进一步验证了算法的正确性。

图1 局部离群数据个数比较Fig.1 Comparison with the count of local outlier

图2 并行算法加速比Fig.2 The acceleration of parallel algorithm

由图2可以看出,随着数据集逐渐增大,并行算法的加速比也逐渐增大,主要是由于算法2的加速比提升引起的。在算法1中,由于属性相关分析基本呈线性变化,加速比基本保持不变;但在算法2中,随着数据量的增大,其单机环境下的微粒群搜索计算量剧增,且增幅远远超过并行子节点中的微粒群搜索,算法2的加速比呈上升趋势。另外,由于并行算法仅进行了4次通信,且属于局域网通信,数据量也较小,所以其网络通信时间几乎可以忽略,这也是算法加速比随着数据集增大而逐渐提高的因素之一。总之,随着数据集的增加,微粒群搜索加速比的提高和网络通信时间的相对较少是并行算法的加速比提高的关键原因。

5 结束语

针对高维海量数据集中的局部离群数据,采用并行计算的思想,给出了一种基于属性相关分析的并行局部离群数据挖掘算法。该算法通过两个并行子算法完成了离群数据的挖掘任务,并在局域网实验环境中,大幅地提高挖掘效率。采用恒星光谱数据作为实验数据,验证了该算法的正确性和有效性。

[1]KNNOR E,NG R.Algorithms for mining distance-based outliers in large datasets[C]//Proc of the 24th VLDB Conference.New York:Morgan Kaufmann,1998:392-403.

[2]HAN J W,KAMBER M.Data Mining Concepts and Techniques[M].San Francisco:Morgan Kaufmann publishers,2001.

[3]BARNETT V,LEWIS T.Outliers in statistical data[M].New York:John Wiley and Sons,1994.

[4]PREPARATA F,SHAMOS M.Computational Geometry:An Introduction[M].USA:Springer-Verlag,1988.

[5]SARAWAGI S,AGRNWAL K,MEGIDDO N.Discovery-driven Exploration of OLAP Data Cubes[C]//Valencia:Proc of Int Conf Extending Database Technology,1998:168-182.

[6]BREUNIG M,KRIGEGL H P,NG R T,SANDER J.LOF:Identifying density-based local outlier[C]//ZytkowJ Med.Rauch Proc of the 3rd European Conference on Principles and Practice of knowledge Discovery in Databases.Prague:Springer,1999:262-270.

[7]AGARARWAL,YU P S.An effective and efficient algorithm for high-dimensional outlier detection[J].The International Journal on Very Large Data Bases,2005,14(2):211-221.

[8]ZHU C,KITAGAWA K,FALOUTSOS C.Example-Based Robust Outlier Detection in High Dimensional Datasets[C]//ICDM'05,2005:829-832.

[9]张继福,蒋义勇,胡立华,等.基于概念格的天体光谱离群数据识别方法[J].自动化学报,2008,34(9):1060-1066.

[10]ZHANG J F,JIANG Y Y,CHANG KAI H.A Concept Lattice Based Outlier Mining Method in Low Dimensional Subspaces[J].Pattern Recognition Letters,2009,30(15):1434-1439.

[11]葛凌云,张继福,蔡江辉.基于微粒群和子空间的离群数据挖掘算法研究[J].系统仿真学报,2009,21(7):1897-1900.

[12]MOHAMED BOUGUESSA,SHENGRUI WANG.Mining Projected Clusters in High-Dimensional Spaces[J].IEEE Transactions On Knowledge And Data Engineering,2009,21(4):507-522.

[13]蔡江辉,张继福.基于聚类的离群数据挖掘及应用[J].太原重型机械学院学报,2004,25(4):254-258.

[14]王玮,张继福.一种基于网格的概念格分布式构造方法[J].太原科技大学学报,2010,31(3):197-201.

[15]王磊.基于属性相关分析的局部离群数据并行挖掘算法研究[D].太原:太原科技大学,2011.

[16]CULLER D,KARP R,PATTERSON D.LogP:Towards a Realistic Model of Parallel Computation[C]//Proc 4th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming.ACM,New York,1993:1-12.

[17]DONGARRA J.Introduction to MPI[J].Int J Supercomputer Applications,1994,8(3/4):169-174.

[18]张继福,赵旭俊.一种基于约束FP树的天体光谱数据相关性分析方法[J].模式识别与人工智能,2009,22(4):639-646.