一种基于加权概念格的分类规则提取算法

2011-08-01孙桂利张继福

太原科技大学学报 2011年5期

孙桂利,张继福

(太原科技大学计算机科学与技术学院,太原030024)

分类是数据挖掘和模式识别等领域中重要的研究内容之一,利用训练数据生成关于类别的描述,即把给定的数据对象映射到某个类,可用于数据对象的分类和预测,具有广泛应用价值。

目前,常用的分类提取算法有:决策树方法,贝叶斯分类法,遗传算法,粗糙集和概念格等方法[1]。决策树方法是通过扫描决策树发现分类知识,适用大规模的数据处理,主要优点是描述简单,分类速度快。如J.R.Quinlan提出的ID3算法[2];贝叶斯分类法是利用概率统计知识进行分类的算法,优点是它可以预测类成员关系的可能性,缺点是由于其假设在实际情况下经常不成立,因而分类准确性就会下降。如NB(Native Bayes)[3];遗传算法优点是具有隐含的并行性,可以和许多方法结合。缺点是收敛于局部和较早收敛问题,而且相对比较复杂;粗糙集其优点是直接从给定问题出发,通过不可分辨关系和不可分辨类来确定问题的近似域,从而找出内在规律,其算法简单,其缺点是很难直接处理连续的属性,如王匡[4]等人提出的决策表约简;概念格是数据分析及分类知识提取的一种有效工具,具有完备性、直观性等特点。胡可云[5]等给出了一般概念格的规则提取方法,其主要原理是依据格结点的直接泛化来产生相应的规则;王浩[6]等给出了基于量化概念格的规则的一种提取方法,提出的量化的相对约简格减少了大规模的概念格的存储复杂度,改算法生成的结果同时剔除了冗余的分类规则;张继福[7]等依据约束概念格[8]结点外延与训练样本数据集等价划分之间的关系,引入外延支持度和划分支持度的概念,提出了一种基于约束概念格的分类规则提取方法,具有较高的分类效率和正确率。冀英伟[14]等提出了一种基于谓词逻辑的分类规则约简方法,消除了冗余规则,提高了效率。王玮[15]等提出了一种基于网格的概念格分布式构造方法,为其在大规模数据集上的应用提供了一种新思路。

目前,在概念格研究中,假定组成概念格的内涵重要性同等重要,没有考虑构成内涵属性重要性的差别,形成的概念格结点中包含很多冗余结点,提取分类规则效率低。为此,张继福[9-11]等人提出了一种新的概念格:加权概念格及其构造方法,加权概念格是针对属性(项目)重要程度的不同,通过引入内涵权值而形成的一种格结构,有效地减低了概念格的存储空间和建格时间。频繁加权概念格是在加权概念格的基础上通过引入虚结点,生成频繁结点和虚结点的格结构,是一个完全格[11]。由于该格结构仅生成满足用户最小权值阈值的结点,具有构造时空复杂性低的特点。由于频繁加权概念格构造中,设置了概念内涵的最小权值阈值,只有满足了最小阈值的频繁结点和虚结点才生出,结点本身就是人们感兴趣的,而不感兴趣的已经被去除掉,也就保证了提取出的知识也就是人们感兴趣的,有价值的。本文采用频繁加权概念格作为分类规则提取工具,给出了一种新的加权分类规则的提取算法。该算法采用加权外延支持度来度量结点外延个数过少且重要程度较低的噪声数据。最后,利用恒星光谱数据作为形式背景,实验验证了该算法有较高的分类正确率。

1 概念格与加权概念格

设K=(D,C,I,W)为一个形式背景,其中:对象集D={t1,t2,…,tn},属性集C={C1,C2,…,Cm},I⊆D ×C,W={w1,w2,…,wm}为C中单属性权值集合,wi∈W标识了属性Ci的重要程度(0≤wi≤1)。参照文献[9-11],其相关定义和概念描述如下:

在形式背景K中,(A1,B1)和(A2,B2)是任意的两个形式概念,如果(A1,B1)≤ (A2,B2)⇔B2⊆B1(A1A2),则由K中的所有概念以及概念之间的偏序关系I可构成了一个完全格,则其称为一般概念格,可表示为＜L(D,C,I),≤＞.设hw=(A,B,w)为K上的任一个三元组,且A⊆D,B⊆C,w为属性集B的权值且0≦w≤1,并满足如下映射关系:

(1)f(A)={c∈ C|∀d ∈ A,〈d,n〉 ∈ I};

(2)g(B)={d ∈ D|∀c∈ B,〈d,n〉 ∈ I}

如果三元组hw=(A,B,w)满足最大扩展性,即f(A)=B,g(B)=A,则称hw为K上的一个加权概念。设h1=(A1,B1,w1)、h2=(A2,B2,w2)是K构造的任意加权概念,如果B2⊆B1(A1⊆A2),则称h1是h2的子孙结点,h2是h1的祖先结点,记为h1≤h2,其中:≤称为概念的“层次序”。如果不存在h3=(A3,B3,w3)使得h1≤h3≤h2,则称h1是h2的子结点,记h1的所有子结点集合为Child(h1),加权概念h2是 h1的父结点,记 h2的所有父结点集合为Parent(h2)。K中所有加权概念及这种序组成的集合称为加权概念格＜L(D,C,I,W),≤＞.设内涵重要性最小阈值(权值阈值)为 θmin(0≤θmin≤1),对于K上的任意加权概念hw=(A,B,w),若w≥θmin,hw称为频繁加权概念;若w ＜θmin,称为非频繁加权概念。

设＜L(D,C,I,W),≤＞由K构造的任意加权概念格,设sup=(D,f(D),w1)为L(D,C,I,W)的最顶结点,Inf=(g(C),C,w2)为L(D,C,I,W)的最底结点,则对于任意非频繁重要结点hw=(A,B,w)且hw≠sup,hw≠Inf:

(1)若Parent(hw)(Child(hw))中只有一个结点sup(Inf),则hw称为次顶概念(次底概念);

(2)若Parent(hw)(Child(hw))中没有sup(Inf),且Parent(hw)(Child(hw))中全为或不全为次顶概念(次底概念),同时 Parent(hw)(Child(hw))中频繁加权概念数不小于2个,则称hw为父虚概念(子虚概念);如果hw既是父虚概念,同时又是子虚概念,则称hw为虚概念(结点),定义虚概念hw的权值为 -1,否则称是非虚概念(结点)。

如果其概念格中每个加权概念均为频繁加权概念或虚概念,则称该加权概念格为频繁加权概念格＜Lf(D,C,I,W),≤ ＞.

2 基于加权概念格的分类规则提取

分类规则提取就是找出从给定数据集D(D={t1,t2,…,tn})到类别属性值的集合C(C={C1,C2,…,Cm})的映射。对于某个待分析的数据集D,其类别属性值是固定的m个,从这个特性方面考虑,可以把数据集分成m个等价划分,记为D1,D2,…,Dm,这时对于每某个记录ti,如果ti中的重要部分从属于Dj,则也就是找到对应的分类Cj,得到分类规则。

设频繁加权概念格的形式背景K =(D,C,I,W),对于任意频繁加权概念格结点均可记为三元组(A,B,w),其中:A⊂D是对象集合,B⊂C是属性集合,w为属性B的权值。对于频繁加权概念格,任意结点都是人们感兴趣的频繁结点或虚结点,从分类规则提取的角度来讲,用户希望提取出的规则应该是使用频率较高的且内涵是重要的。但现实生活中,往往出现情况是规则较重要但使用频率非常低,或者规则一般重要但是使用频率较高。重要程度和使用频率两者结合可以很好的解决这种问题,重要性一般且使用频率频率较低的分类规则就可看成是无意义规则,而高于这个限度的规则视为有意义规则。结合频繁加权概念格可知:格结点的内涵的权值的意义就代表着重要程度;格结点的外延个数就是其内涵所包含的数据对相个数较少,从中提取出的分类的规则使用频率就低。

定义1 设(A,B,w)为频繁加权概念格中的任意结点,格结点的加权外延支持度定义为E=w*|A|/|U|,其中:|A|为结点外延包含对象的个数,|U|为总记录的条数。

对于任意频繁加权概念格结点,加权外延支持度E表示的是格结点的内涵的重要程度同其外延中的数据对象在形式背景中出现概率的两者结合。E越高代表从B中提取的分类规则很重要且能够对较多数据对象进行分类,即:实用性越强,这样所提取出的规则对于用户是非常有意义的。如果E非常低,则实用性非常低,所提取出的规则使用频率很低或重要性不够,这样的格结点可视为无用规则或噪声。所以,可设定加权外延支持度阈值Emin,大于Emin的被认为满足实用性,从而可有效的减少噪声,满足用户的要求。另一方面,在A满足外延加权支持度大于Emin情况下,在提取分类规则时,肯定会碰到格结点中的外延对象所对应的类别属性属于多种类别属性的情况。对于这样的格结点,判断其属于哪种类别属性非常重要,由于各个类别属性的权值不同,同时外延对象属于不同类别属性的概率也是不同的。为便于下一步确定分类规则的分类属性取值。对于任意结点的外延对象可能属于不同的类别属性,可以从两个方面考虑:

当A⊂Di时,任意结点的外延完全从属于某个划分Di,则A中对象的所对应分类属性值一定是Di所对应的分类属性值Ci(1≤i≤m),则可提取出分类规则B→Ci;

当A⊄Di且A∩Di=Φ,任意结点的外延不完全从属于某个划分Di,A中对象的分类属性值不一定是Di所对应的分类属性值Ci(i=1,…,m),这里可以定义A中对象从属于各类别属性的概率,可定义为划分度Pj,Pj是满足内涵B且属于Ci的对象的个数同结点外延包含对象的个数的比值。其中一定能找到最大的划分度Pj,表示满足内涵B且属于Cj的对象个数最多,但它不能直接选取其作为可提取的规则,因为内涵的重要性是不同的,满足对象的最多的但是不是最重要的、不是人们所需要的规则。同理,只取内涵最重要的同样不能作为选取分类规则的标准。人们最想要的是权重和划分支持度同样高的。这也是频繁加权概念格的重要意义所在,所以,这里引入重要性概念,作为判别依据。

定义2 对于频繁加权概念格中的任意结点(A,B,w),如果 ∃g∈A,g∈Cj(1≤j≤m),wg为Cj对应的权值,M=A∩Cj,H=|M|*wg为A中对象的分类属性值取Cj的重要性。

A中数据对象的分类属性属于不同的类别属性,划分支持度描述了其属于不同类别属性的概率,划分支持度大的权重反而小的所对应的规则并不是我们所需要的。而权重大划分支持度小的准确性不高。所以两者综合考虑才能选取最适当的规则。

定理1 对于频繁加权概念格中的任意结点(A,B,w),存在 g∈A,g∈Ci(1≤i≤m),如果A中任意一个k∈A,k∈Cj(1≤j≤m),都有Hg=|M|*wg＞Hk=|N|*wk,其中M=A∩Ci,N=A∩ Cj,wg为Ci对应的权值,wk为Cj对应的权值,则此结点分类规则为B→Ci.

证明对于任意结点(A,B,w),存在g∈A,g∈Ci,由定义2可知,A中对象的分类属性值取Ci的重要性为Hg=|M|*wg.而任意一个k∈A,k∈Cj的分类属性值取Cj的重要性Hk=|N|*wk.如果Hg＞Hk,也就是Hg是A中对象的分类属性取值重要性最大的。即可得出结论:此结点分类规则为B→Ci.

由定理1可知,A中数据对象属于不同的类别属性时,分别求取其分类属性值为Ci的重要性,选取重要性最大的那个类别属性,提取分类规则B→ti,选取的分类属性准确性就高。

3 基于加权概念格的分类规则提取算法

综上所述,从频繁加权概念格中提取分类规则的基本思想是自顶向下逐个扫描每个结点,在结点的加强外延支持度大于Emin情况下,当结点外延包含于某个数据集等价划分时,直接提取规则,当结点外延不包含于某个数据集等价划分时,判断其属于某个类别属性的重要性,选取重要性最大的作为分类规则的分类属性。其算法描述如下:

算法:频繁加权概念格分类算法CRAAFWCL(Classification rule acquisition algorithm based on Fre-quent Weighted concept lattice)

输入:频繁加权概念格k,加权外延支持度阈值Emin

输出:分类规则集rule

//总对象个数为N;同分类属性的m个不同取值可分为m个等价划分(D1,D2…Dm)

该算法根据加权外延支持度采用自顶向下计算每个频繁加权概念格结点,判断其外延与等价划分的关系,如果外延包含于某等价划分Gi,直接提取规则,否则计算其外延与Gi相交的关系,有交集的计算占据的比例乘以对应的权值得到它对应得比重,从中选择最大的值P对应得规则,进而提取分类规则,然后继续扫描其他结点。算法扫描每个结点的时间复杂度是O(n),每个结点外延A与Gi交运算时间复杂度为O(m),每个结点提取分类规则复杂度为O(m2)。因此,次算法时间复杂度为O(m2*n)。

4 实验结果及分析

实验环境:CPU:Pentium(R)D-3.0G CPU,内存:512M,操作系统:Windows XP SP3,数据库:ORACLE9i,采用Microsoft Visual Studio C++2008实现了频繁加权概念格分类算法CRAAFWCL。此恒星光谱数据是利用国家天文台提供的,分类属性取恒星的7个类型,频繁加权概念格的形式背景通过以下预处理构成:①选取200个的波长作为条件属性集,②每一波长处依据流量和峰宽把其离散化为13中数一作为条件属性。其中:一半作为训练集,一半作为测试集。参考文献[11,13],采用归一化的信息熵做为单属性内涵的权值,用户也可以自己设定权值,而多属性内涵的权值采用算术平均权值的方法。

表1 分类规则测试1Tab.1 Test 1 of classification rule(权值阈值 θmin=0.01,恒星光谱个数 =4 000条)

表2 分类规则测试2Tab.2 Test 2 of classification rule(外延加权支持度Emin=0.002 2,恒星光谱个数=4 000条)

外延加权支持代表着所提取规则的使用频率和内涵重要程度,从表1中可以看出,其取值对分类规则的提前具有很大的影响,随着外延加权支持度阈值的逐渐增加,其所提取的规则内涵越重要,使用频率越高,但是满足条件能提取的规则逐渐减少,其正确率也逐渐减少,所以选取适当的加权外延支持度阈值就非常的重要,要选取能满足用户对提取的规则时使用频率较高的且内涵是重要的最低要求,从而保证所提取分类规则的正确率。从表2和表3中可以看出,随着数据集的数据量的逐步增加,生成的概念格结点也同样的增多,同样提取出的分类规则也就越多。但人们一般只希望对重要属性感兴趣,频繁加权概念格引入虚结点,生成频繁结点和虚结点的格结构,由于该格结构仅生成满足用户权值阈值的结点,所以其构造时间和存储空间大大缩短。加权阈值设置就可把人们关心的数据给提取出来,从表中看到,随着权值阈值设置的提高,生成的频繁加权概念格的结点有一个下降的变化趋势,即随着权值阈值设置的升高,满足条件的频繁加权概念格结点也逐步减少,所提取的分类规则数也逐渐减少,因此权值阈值的设置对系统有很大的影响,随着数据量的增加,生成的结点增多,所产生的分类规则也多,所用的时间也就增多。由此可见,随着适当的权值阈值设置,满足权值阈值的结点数减少,相应地频繁结点和虚结点的总个数不断下降,构造格的时空复杂性越低,因此所提取的规则的效率也就相应的提高。

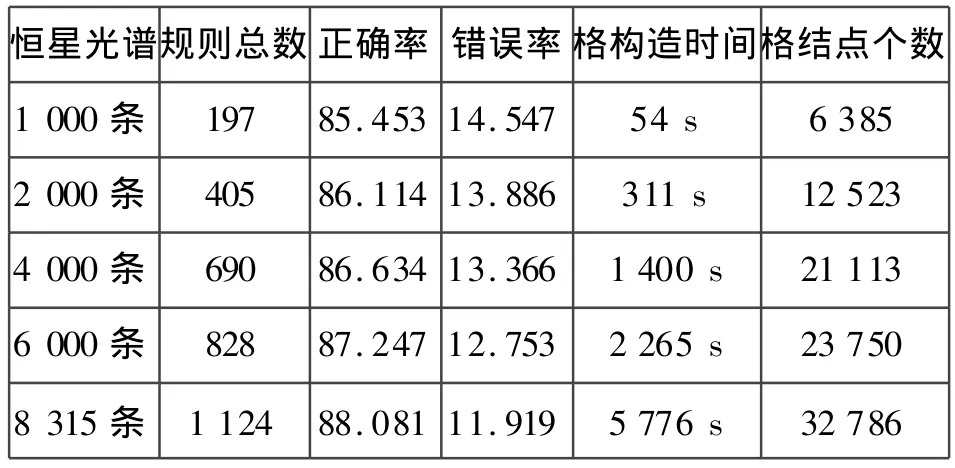
表3 分类规则测试3Tab.3 Test 3 of classification rule(权值阈值θmin=0.01,外延加权支持度Emin=0.002 2)

5 结束语

频繁加权概念格是针对属性的重要程度的一个完全格,该格结构具有构造时空复杂性低且提取的知识的实用性强的特点。本文采用频繁加权概念格作为分类规则提取工具,通过引入加权外延支持度的概念,给出了一种新的加权分类规则的提取算法CRAAFWCL。该算法计算加权外延支持度作为提取分类规则的重要依据来提取分类规则。最后利用国家天文台提供的恒星光谱数据,实验验证了该算法具有较高的分类效果。

[1]Jiawei Han.数据挖掘概念与技术[M].2版.范明,译.北京:机械工业出版社,2004.

[2]Quinlan J R.Induction of decision trees[J].Machine Learning,1986,1(1):81-106.

[3]Friedman N,Geiger D,Goldszmidt M,Bayesian network classifier[J].Machine Learning,1997,29(1):131-163.

[4]王国胤,于洪,杨大春.基于条件信息熵的决策表约简[J].计算机学报,2002,25(7):759-766.

[5]王志海,胡可云,胡学钢.概念格上提取规则的一般算法与渐进式算法[J].计算机学报,1999,22(l):66-70.

[6]王浩,胡学钢,赵文兵.基于量化相对约简格的分类规则发现[J].复旦大学学报,2004,43(5):761-765.

[7]张继福,马洋.一种基于约束概念格的恒星光谱数据自动分类方法[J].光谱学与光谱分析,2010,30(2):559-562.

[8]张继福,张素兰,胡立华.约束概念格及其构造方法[J].智能系统学报,2006,2(1):31-38.

[9]张继福,张素兰,郑链.加权概念格及其渐进式构造[J].模式识别与人工智能,2005,18(2):171-176.

[10]张素兰,张继福,高愫邡.加权概念格的渐进式构造及其关联规则提取[J].计算机工程与应用,2005,41(7):173-178.

[11]王欣欣,张继福,张素兰.一种频繁加权概念格的批处理构造算法[J].模式识别与人工智能,2010,23(5):77-81.

[12]胡可云,陆玉昌,石纯一.基于概念格的分类和关联规则的集成挖掘方法[J].软件学报,2000,11(11):1478-1484.