电磁层析成像中基于半周期采样的数字解调方法
2011-08-01尹武良王化祥
尹武良,王 奔,王化祥
(天津大学电气与自动化工程学院,天津 300072)
电学层析成像是一种通过在物体边缘进行电、磁测量而得到物体内二维分布的层析成像方法.它包含 3个主要模态,即电容层析成像(electrical capacitance tomography,ECT)、电阻层析成像(electrical resistance tomography,ERT)及电磁层析成像(electromagnetic tomography,EMT)[1].EMT 广泛应用于工业过程的可视化[2-3]及生物层析成像测量[4-6].EMT传感器由一组8个或16个均匀分布在物体外围的线圈组成,通过线圈之间互感和自感的测量而进行图像重建.
相敏解调[7]是从接收线圈测得的电压信号中提取幅值和相位信息的过程,是电磁层析成像技术的重要环节.数字解调是由高速 A/D转换器对被测信号采样,利用高性能数字信号处理器件,如 FPGA、DSP等,采用数值计算的方法提取被测信号的幅值和相位信息的过程.常用的解调方法有快速傅里叶变换(fast Fourier transform,FFT)解调和正交序列解调.正交序列解调[8-10]可以看作是FFT解调在数学上的简化,它克服了模拟电路固有的误差和系统的不稳定性,满足信号分析所要求的高性能和快速测量等[11-12].
一般地,参考信号是预先计算好的正余弦函数值,存储在处理器内,因此,解调过程即为查表求取离散的正、余弦参考值,并同采集到的信号相乘、累加的过程.通常,电学层析成像运用整周期的倍数采样进行正交序列解调,本文提出了采样半周期的正交序列解调方法,给出了基于 Matlab的仿真结果和基于实际硬件系统的实验结果,并从频域的角度给出了理论解释.采样半周期明显提高了信号解调速度,改进了图像采集的实时性.这对 EMT以及 ECT、ERT有重要的意义.
1 理论分析
1.1 正交序列解调的FFT解释
定义同相参考信号 ()r n、正交参考信号 ()q n及被解调信号 ()s n分别为

式中:N为整周期采样点数;θ为初始相位.则同相分量为
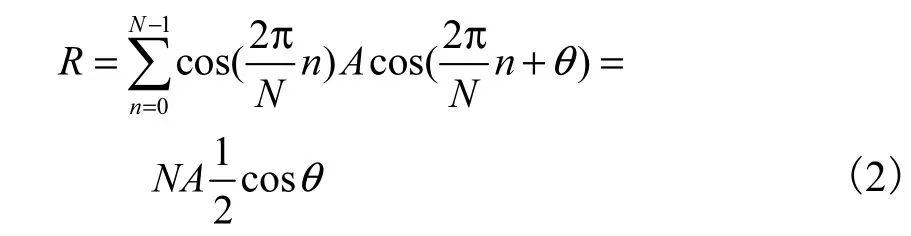
正交分量为
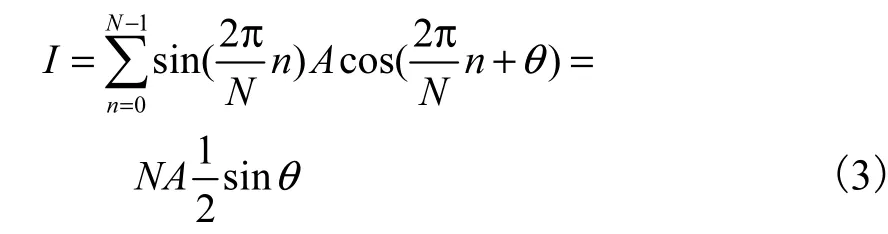
具体实现中,参考信号是预先计算好的正、余弦函数值,因此,解调即为被解调信号与参考信号的相乘和累加的过程.
对比 FFT运算,假设仅通过单周期的被测数据进行解调,即
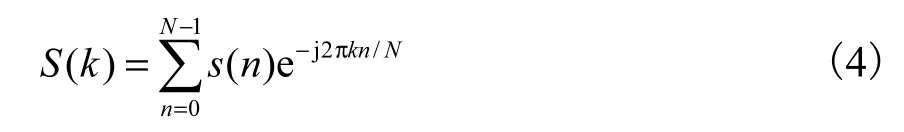
当k=1时,有
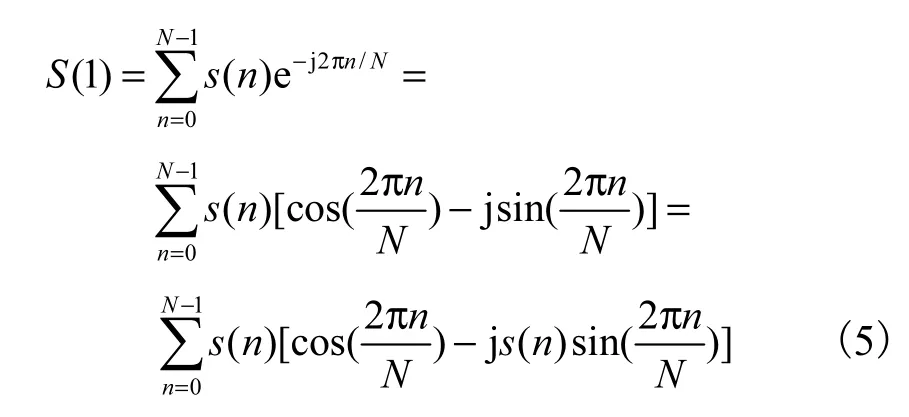
可见 (1)S 的实部、虚部分别为R和I,这与上述正交序列解调的结果相同.而与FFT解调相比,数字正交序列解调的计算量明显降低,对于整数周期内连续的N个采样点,正交解调仅需进行2N次实数乘法和2N次累加运算.
通常而言,采样周期越多,解调的精度越好,抗噪声能力越好,而测量的实时性会下降.周期的选择要根据系统的设计要求进行调整.
1.2 正交序列解调的频域解释
假设 s( t) = Asin(ω t+ϕ )为被解调信号,则根据乘法解调的公式
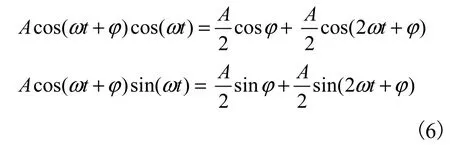
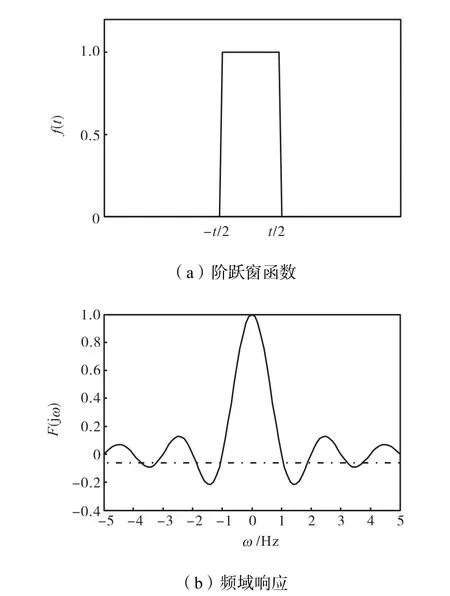
图1 阶跃窗函数和频域响应Fig.1 Step function and frequency response
不难看出,将 2倍频信号滤波去除之后,乘法器的输出即为解调需要的结果,即被解调信号的实部和虚部.
在数字正交解调中,对于相乘后信号的整周期进行叠加,等效于使之与阶跃窗函数进行卷积,而时域的卷积对应于频域内的相乘;阶跃窗函数在频域中存在许多零点,当阶跃窗函数的长度为整周期时,其中的一个零点正好在2倍频处,于是可将2倍频信号完全消除,因此信号数字正交解调后便获得原信号的实部和虚部.
由图1可见,如果采样信号的一个整周期进行解调,便利用了第 2个频率过零点;由此可以推论,利用第 1个频率过零点,便可实现采样半周期对信号解调,这样,信号解调速度至少可以提高 1倍,相应的图像采集数也增加1倍.图2为利用Matlab对半周期信号解调的结果,

图2 相位超前30°、幅值为3的半周期正弦信号Fig.2 Half-period sinusoidal signal with phase ahead 30 degree,amplitude equal to 3
利用一个周期的数据进行解调的公式为
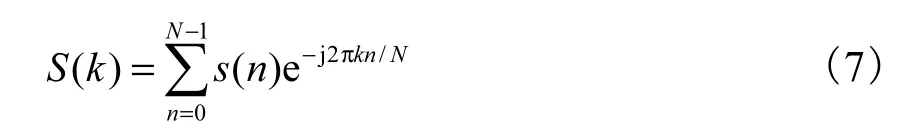
当k=1时,有
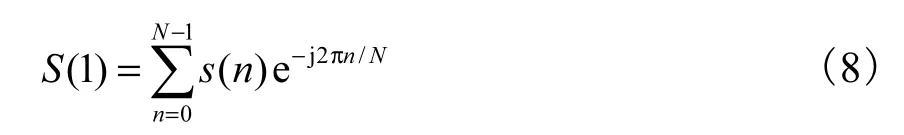
对于半周期采样解调,假设式(1)中的 N为单周期采样数,式(2)和式(3)可转化为可简化为
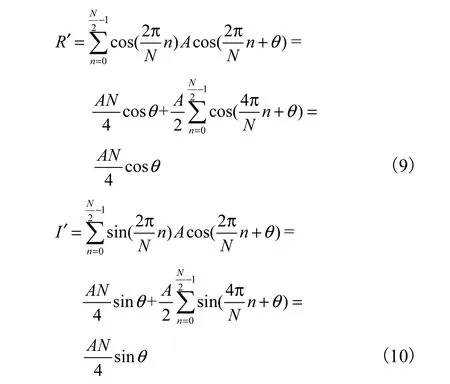
由式(9)和式(10)可得

利用半周期解调的技术,对于 8线圈系统,如果在100,kHz激励频率下,那么理论上每秒钟最大可采集3,572幅实时数据用于图像重建.
2 仿真与实验
2.1 正交序列解调Matlab仿真
由图 3和图 4可见,当采样的点数任意时,A、φ的值呈现震荡现象.值得注意的是,在Matlab仿真下,采用正交序列解调算法,采样半个周期同样可解调出输入信号的相位和幅值,分别为和 1(图中虚线所示),图中,当横轴取 2时,即采样半周期.可见Matlab仿真证实了第1.2节的理论分析.
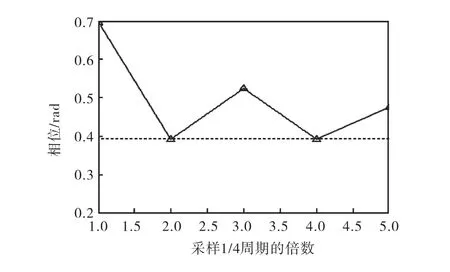
图3 相位解调结果Fig.3 Demodulation result of phase

图4 幅值解调结果Fig.4 Demodulation result of amplitude
2.2 正交序列解调仿真实验
本实验采用天津大学数字电磁层析成像系统,如图5和图6所示.由DDS模块产生频率10 kHz的正弦波,A/D 转换器的采样频率为 10,MHz,即每个周期采样1,000个点.通过半周期解调与整周期解调结果的比较,验证半周期采样解调方法的可行性.将FPGA中 IP核的参数分别设置为 500和 1,000,即MAC的累加个数为500和1,000.直接使用DDS产生的正弦和余弦参考序列对该正弦信号解调,这里共测量了 56次,正弦和余弦解调对比结果分别如图 7和图8所示,数据如表1和表2所示.
图7和图8中的数据1分别代表了采样半周期时,解调信号的实部和虚部值(16位的二进制数);数据2分别代表了采样整周期时,解调信号的实部和虚部值.比较被解调信号的实部和虚部等同于其幅值和相位.

图5 数字EMT系统Fig.5 Digital EMT system

图6 EMT系统传感器示意Fig.6 Sensor schemes of EMT system

图7 正弦参考信号解调对比Fig.7 Comparison of sinusoidal reference signal

图8 余弦参考信号解调对比Fig.8 Comparison of cosinusoidal reference signal

表1 采样半周期的实部与虚部解调结果Tab.1 Real and Imaginary part demodulation results of half-period sampling
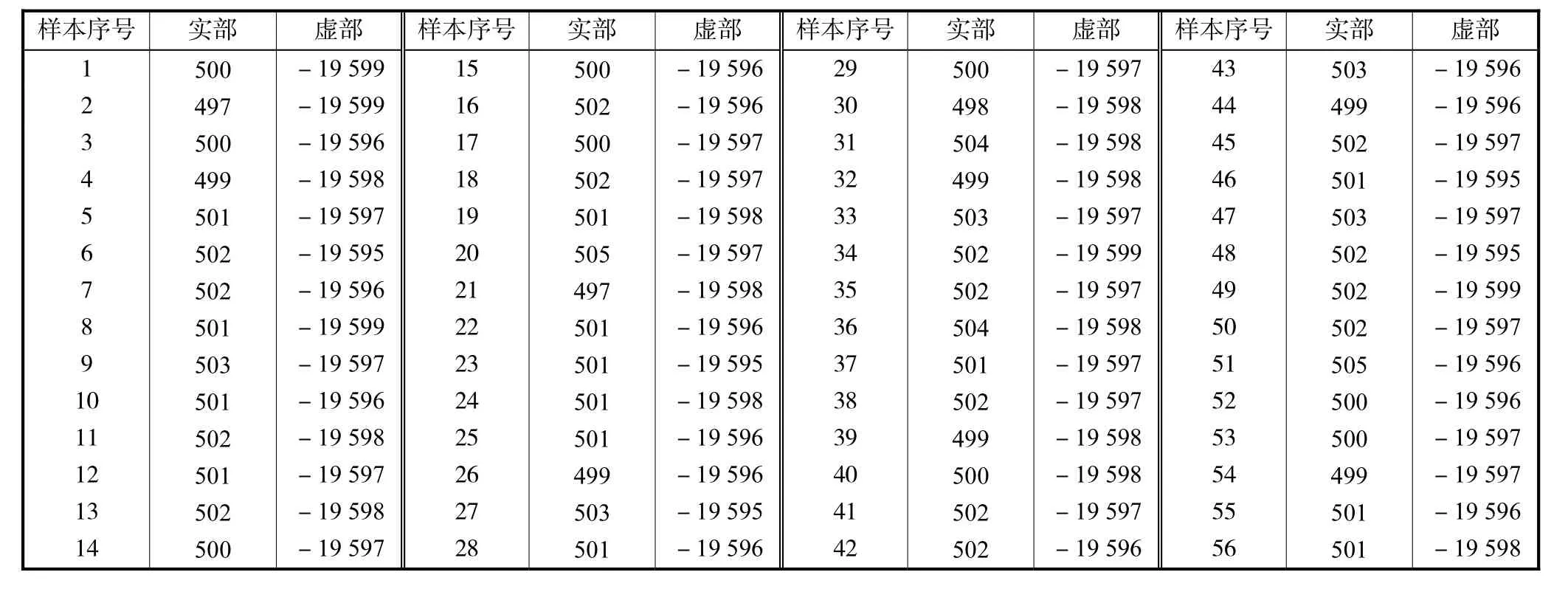
表2 采样整周期的实部和虚部解调结果Tab.2 Real and Imaginary part demodulation results of full-period sampling
分别对表 1、表 2的 56组测量数据进行比较,2组数据相似度高,实部变化在 1%以内,虚部变化在0.025%以内.这也直观地解释了采样半周期解调的可行性.从图中还可知采样整周期解调的振荡幅度比半周期解调的小,因为采样点数增加会引起抗噪声能力增强.但是在一些要求成像速度较高的应用(比如钢水流型检测、高速流体成像)中,半周期解调能提高解调的速度以及后续成像的速度,是一种有潜力的方法.
2.3 成像实验结果
基于第2.2节的数字EMT系统,在传感器(如图8所示)内放置铝棒和铜棒进行成像实验,其中铝的电导率为3 . 82× 107S/m,铜的电导率为5.80× 107S/m.本实验使用直径为 12.5,mm的铜棒和铝棒,采用灵敏度系数法进行图像重建.成像结果如表3所示.

表3 基于实际硬件系统的成像结果Tab.3 Imaging results based on real hardware system
基于半周期采样的正交序列解调方法通过减少采样点数量,提高采样速度,改进图像采集的实时性.由表 3清晰可见,这种方法成像与整周期采样成像没有显著差别,同样能得到较好的重建图像.这为半周期采样解调运用在一些要求成像速度较高的场合提供了依据.
3 结 语
针对数字正交序列解调,本文在进行频域分析的基础上,从理论上解释了正交序列解调.并且从实验、Matlab仿真以及理论上验证了采样半周期正交序列解调的可行性和有效性.半周期采样相比于通常的整周期倍数采样,解调速度至少可以提高1倍,单位时间相应重建图像幅数也可以增加1倍.它可应用于一些对速度要求较高的成像中(比如钢水流型检测、高速流体成像),半周期采样解调是一种有潜力的方法.
[1] Griffiths H. Magnetic induction tomography[J]. Meas Sci and Technol,2001,12(8):1126-1131.
[2] Binns R,Alyons A R,Peyton A J,et al. Imaging molten steel flow profiles[J]. Meas Sci Technol,2001,12(8):1132-1138.
[3] Ma X,Peyton A J,Higson S R,et al. Hardware and software design for an electromagnetic induction tomography(EMT)system for high contrast metal process applications[J]. Meas Sci Technol,2006,17(1):111-118.
[4] Peyton A J,Mackin R,Goss D,et al. Addressing the difficulties in using inductive methods to evaluating human body composition[J]. Biometrie Humaine at Anthropologie,2003,21:63-71.
[5] Yin W L,Peyton A J,Zysko G,et al. Limits of the weakly coupled field assumption for low conductivity electromagnetic induction tomography[J]. Bibliogr,2009,114(6):75-79.
[6] Griffiths H,Stewart W R,Gough W. Magnetic induction tomography:A measuring system for biological tissues[J]. Ann NY Acad Sci,1999,873(2):335-345.
[7] Oh Tong In,Lee Jeong Whan,Kim Kyu Sik,et al.Digital phase-sensitive demodulator for electrical impedance tomography[C]// Proceedings of the 25th Annual International Conference of the IEEE EMBS. Cancun,Mexico,2003:1070-1072.
[8] 张雪辉,王化祥. 电容层析成像中的相敏解调[J].微计算机信息,2008,7(2):300-302.Zhang Xuehui,Wang Huaxiang. Phase sensitive demodulation in ECT system[J]. Microcomputer Information,2008,7(2):300-302(in Chinese).
[9] Masciotti J M,Lasker J M,Hielscher A H. Digital lock-in detection for discriminating multiple modulation frequencies with high accuracy and computational efficiency[J]. IEEE Transactions on Instrumentation and Measurement,2007,57(1):182-189.
[10] Barone F,Calloni E,Difiore L,et al. Highperformance modular digital lock-in amplifier[J]. Rev Sci Instrum,1995,66(6):3697-3702.
[11] Smith R W M,Freeston I L,Brown B H,et al. Design of a phase-sensitive detector to maximize signal-to-noise ratio in the presence of Gaussian wideband noise[J].Meas Sci Technol,1992,3(11):1054-1062.
[12] Sonnaillon M O,Bonetto F J. A low cost,high performance,DSP-based lock-in amplifier capable of measuring multiple frequency sweeps simultaneously[J].Rev Sci Instrum,2005,76(4):24703-24710.
