水平管降膜蒸发器壳程流场和温度场数值研究
2011-08-01侯昊毕勤成张晓兰
侯昊,毕勤成,张晓兰
(西安交通大学 动力工程多相流国家重点实验室,陕西 西安,710049)
淡水资源匮乏已成为当今世界威胁人类生存的严重问题。在地球的水资源总量中海水占97.5 %,从某种意义上说,海水是取之不尽、用之不竭的主要水源。因而,发展海水淡化技术,向海洋要淡水是解决淡水资源供需矛盾的有效途径。海水淡化也就成为开发淡水资源的重要途径之一。目前,已商业化的海水淡化方法有多种[1-2],其中,低温多效蒸馏海水淡化技术不仅热能利用率高、产水率高,而且节能,近年来发展迅速,装置规模日益扩大。另外,由于采用廉价材料,成本也日益降低,使其成为较为理想的海水淡化方式。因此,这种海水淡化技术备受各国学者的关注,成为当前海水淡化领域的研究热点之一[3-5]。作为低温多效蒸馏海水淡化系统的重要装置,水平管降膜蒸发器受管内蒸汽和管外海水的热工参数影响,壳程流场处于复杂的三维流动状态,每一局部区域都经历变质量的流动、热力和传热过程,并且流动与换热相互耦合,因此整个热力过程错综复杂。另外,几何结构复杂,又封闭在壳体内部,无法观察和测量蒸发器内部所有位置的流场数据,一方面使研究者很难全面了解其内部工作过程,准确掌握整体以及局部区域真实流动和传热状况的细观信息;另一方面,又制约了试验数据对于蒸发器结构改进和运行参数优化的指导作用。随着多物理场耦合技术的发展,分布参数法因其能够描述实际物理过程,获得更加真实准确的参数分布,受到越来越多的重视。国内外一些学者已经将该方法应用于某些换热器的热力性能分析和优化设计[6-10],而将其用于水平管降膜蒸发器的研究却鲜有报道。为此,本文作者构建了水平管降膜蒸发器实体的三维分布参数模型,对蒸发器壳程区域的流场和温度场特性进行了数值研究,分析和总结了该区域内流体流动和传热的细观规律,直观地刻画了蒸发器内部的热力过程,为深入了解复杂流动与传热现象提供了理论指导。
1 物理模型
图1所示为水平管降膜蒸发器示意图,其中管束分2个管程布置,1管程布置在下部,2管程在上部。换热过程分为管内蒸汽冷凝和管外海水蒸发2部分:一方面,加热蒸汽首先进入1管程并大部分冷凝,剩余蒸汽经管箱折返后进入2管程直至完全冷凝;另一方面,海水通过喷头分布到管束上,自上而下降膜流动并逐渐吸收热量,由过冷变为饱和状态后开始蒸发。产生的二次蒸汽由管束周边逸出,然后穿过丝网除沫器;在去除蒸汽中夹带的海水液滴后,进入壳体两侧的蒸汽通道,并沿管束轴向流出。分管程布管在热力学上是合理的,可以减小冷热流体传热温差,减少熵增引起的热损失,另外,管内蒸汽压力高于管外二次蒸汽压力,即使传热管因腐蚀穿透也能保证产品水水质。

图1 水平管降膜蒸发器示意图Fig.1 Schematic of horizontal-tube falling-film evaporator
2 数学模型
2.1 基本假设
为了使模型推导方便,模型建立基于以下假设:(1) 忽略管排间液体的飞溅,即上排管底部落下的液量等于下排管顶部的初始液量;(2) 汽液界面处于热力学平衡状态,不考虑蒸汽的剪切力作用;(3) 不考虑传热管的污垢热阻。
2.2 计算单元划分
对于蒸发器内部不同区域的管束而言,管内蒸汽干度沿管子轴向逐渐减小,管外喷淋海水流量沿管排方向变化,从而造成蒸发器的换热性能沿管子轴向和管排方向均有变化。管束示意图如图2所示。将蒸发器内管束从i,j,k3个方向分别划分为Nx,Ny,Nz等份,其中i,j,k分别表示水平、垂直和轴向方向,这样整个管束划分为Nx×Ny×Nz个计算单元。这种方法的优点在于数学模型的尺度基于物理模型的实际拓扑结构,具有明确的物理意义,避免陷入CFD方法过于繁琐的计算,极大地提高计算速度和加快程序收敛。针对每一单元建立传热与流动控制方程,使该单元出口参数成为下一单元的入口参数,采用迭代法求解出所有单元进出口的温度、压力等热力参数。每一计算单元的热负荷为:

式中:hoveral,hi和ho分别为总传热系数、管内和管外传热系数;A为传热面积;λ为导热系数;Ti和To分别为管内、外工质热力学温度;di和do分别为管内、外直径。

图2 管束示意图Fig.2 Schematic of tube bundle
为了计算每一单元的热负荷和确定出口干度,需考虑蒸汽沿管子轴向和海水沿管排方向各热工参数的变化,将物性、传热、流动等条件实现局部化,从而统一管内外侧相变与非相变情况下的计算,分别获得管内、外传热系数分布。另外,管内蒸汽的压力、温度变化与两相压降有关,因而还需计算管内汽液两相压降。
2.3 管内、外传热系数
2.3.1 管内传热系数
蒸汽进入管束时为饱和状态,随着热交换的进行,经历汽液两相流和单相液体状态。当蒸汽处于汽液两相时,Chato[11]在Nusselt冷凝换热理论基础上进行解析,得到了水平圆管周向平均传热系数,Jaster等[12]又对其进行了修正,由此得到管内传热系数公式如下:
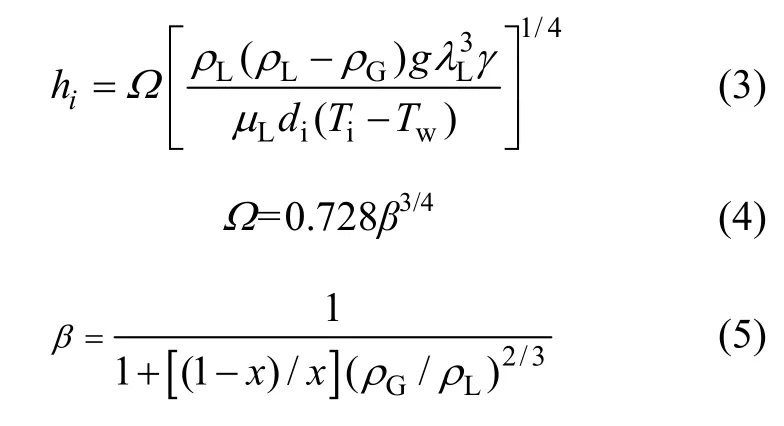
式中:ρL和ρG分别为工质液相和气相的密度;r为汽化潜热;μL为液相动力黏度;g为重力加速度;Tw为管子内壁面热力学温度;x为汽液两相流干度。
当管内蒸汽完全冷凝后,管内传热系数采用齐德-泰勒公式[13]进行计算:

式中:l为管子长度;μw的定性温度为管子内壁面热力学温度。
2.3.2 管外传热系数
海水进入蒸发器为过冷状态,沿管排降膜并逐渐吸热后达到饱和状态。对于管外液膜处于过冷状态,采用如下公式[14]进行计算:
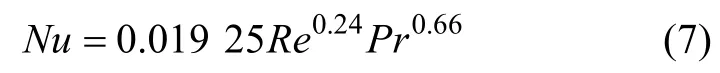
对于管外液膜处于饱和状态,采用如下公式[15]进行计算:
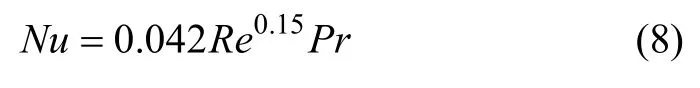
2.4 两相压降
水平管内汽液两相流动压降由重位压降 Δpstatic、加速压降Δpmom和摩擦压降Δpfrict组成,即:
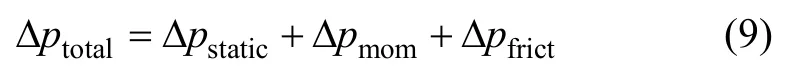
由于是水平管,重位压降Δpstatic=0,加速压降为:
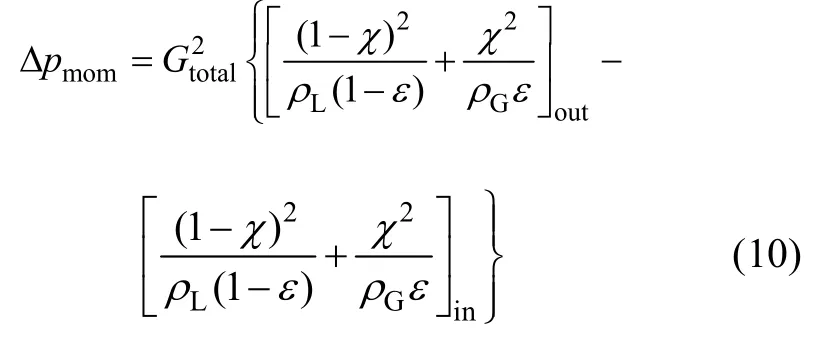
式中:Gtotal为液汽两相流总质量流速;ε为空泡份额;下标in和out表示计算单元的进口和出口。
摩擦压降采用Friedel公式[16]进行计算:

式中:ΔpL为液相摩擦压降;φ2为两相摩擦倍率。
3 程序计算方法
根据上述计算模型,再加上对热力过程其他一些现象的数学描述及求解,开发了水平管降膜蒸发器三维稳态过程的数值计算程序,能够模拟不同几何结构和流体物性参数条件下蒸发器内部流动与传热过程,具体计算步骤如下。
步骤 1 输入已知条件:包括蒸发器几何结构参数(传热管规格以及管排布置结构)、加热蒸汽和供入海水各热工参数和相关物性参数;
步骤2 对蒸发器管束划分计算单元;
步骤3 预估管外饱和压力、2管程蒸汽进口压力和流量;
步骤4 依次求解2管程和1管程各排管的热工参数,针对任一排管,先按照轴向顺序分别计算各个单元,然后沿管排方向转至下一排管进行计算,直到蒸发器的底排管;
步骤5 根据算得的管外饱和压力、2管程蒸汽进口压力和流量代替旧值,重新迭代计算直至收敛。
4 计算结果及分析
4.1 模型验证
为了验证模型及程序的正确性与可靠性,本文对某低温多效海水淡化系统的水平管降膜蒸发器进行了模拟,计算中一共划分单元26 970个,满足网格独立性要求,并将计算结果与该蒸发器的实际运行工况进行比较。图3所示为计算值与实际值的对比。由图3可见:在加热蒸汽和海水参数相同的条件下,本文计算所得二次蒸汽参数与实际工况吻合良好,两者之间的相对误差在-4.2%~1.6 %范围内,证明了本文所用模型具有很高的准确度。
4.2 海水流场及喷头布置的影响
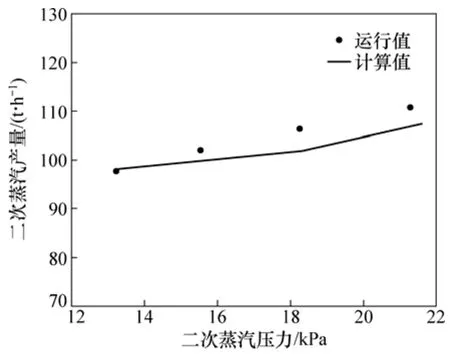
图3 计算值与实际值的对比Fig.3 Comparison between calculated and actual results
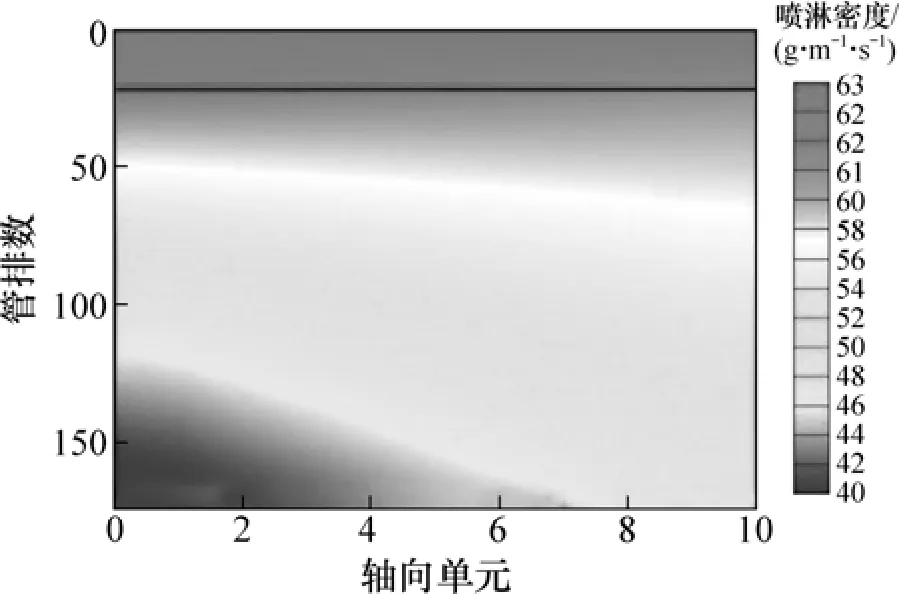
图4 海水流场分布Fig.4 Distribution of seawater flow field
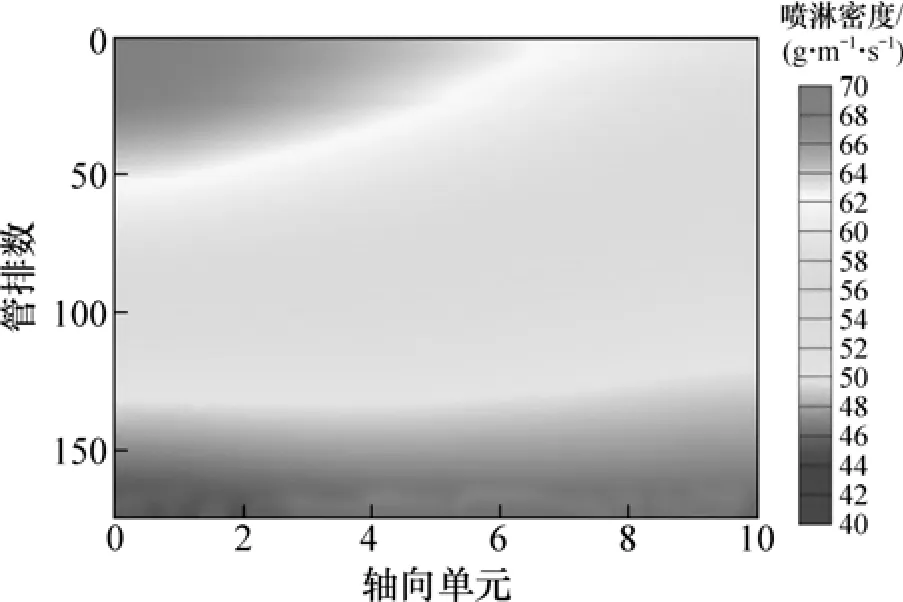
图5 改进喷头布置后海水流场分布Fig.5 Distribution of seawater flow field for changing placement of spray nozzles
图4和图5所示为不同喷头布置方式下蒸发器内海水流场云图,直观地给出了海水喷淋密度沿管排方向分布的完整数据。由图4和5可知:蒸发器内喷头布液效果良好,降膜传热过程顺畅进行。由图4可知:蒸发器采用均匀喷头布置方式时,海水喷淋密度由上部的63 g/(ms)减小到下部的 40 g/(ms),呈现出“上高下低”的分布规律,其原因在于过冷的海水需要2管程蒸汽加热后才能达到饱和状态,而且由于2管程蒸汽量较少,其换热量也较少,即使海水已经饱和,产汽量也非常小,因此海水喷淋密度在2管程时大体上保持不变。到达1管程后,海水开始蒸发,产生二次蒸汽。在1管程中部海水喷淋密度由60 g/(ms)逐渐降低到46 g/(ms),而且整体变化较为平稳,说明此区域换热效果良好,产汽量保持稳定;而在1管程进口的下半区海水喷淋密度已经很小,其最小值为40 g/(ms),但仍能够保证传热管束周向完全润湿,不会引起液膜破裂。同时,在该区域海水喷淋密度沿管长方向由40 g/(ms)逐渐增大到50 g/(ms),表现出分布不均匀的特点,不利于避免“干斑”现象发生。因此,可以采用“前密后疏”的喷头布置方式来改善这一区域的海水流动情况。如图5所示,2管程上部区域海水分布不均,喷淋密度对应地由 70 g/(ms)逐渐减小到 60 g/(ms),而1管程下部区域海水分布则更加均匀,喷淋密度大体上保持不变,约为48 g/(ms)。
4.3 海水温度场
图6所示为蒸发器内海水温度场云图,过冷的海水由50 ℃逐渐达到饱和温度57 ℃,说明2管程已经达到了对海水的预热作用。在2管程出口的上半区海水温度始终保持在50 ℃,这是因为管内蒸汽已经完全冷凝,两相换热变为单相换热,过冷海水无法得到足够热量使其温度明显上升,还要继续吸热才能达到饱和状态。根据能量守恒原理,加热蒸汽带入的热量等于进出口海水变化的热量与二次蒸汽带走的热量之和,因此,可以通过对海水进行预热提高海水的初始温度来有效减小其过冷度,进而增大二次蒸汽所占的热量份额,提高加热蒸汽的热利用率,从而增加单效蒸发器的二次蒸汽产量。
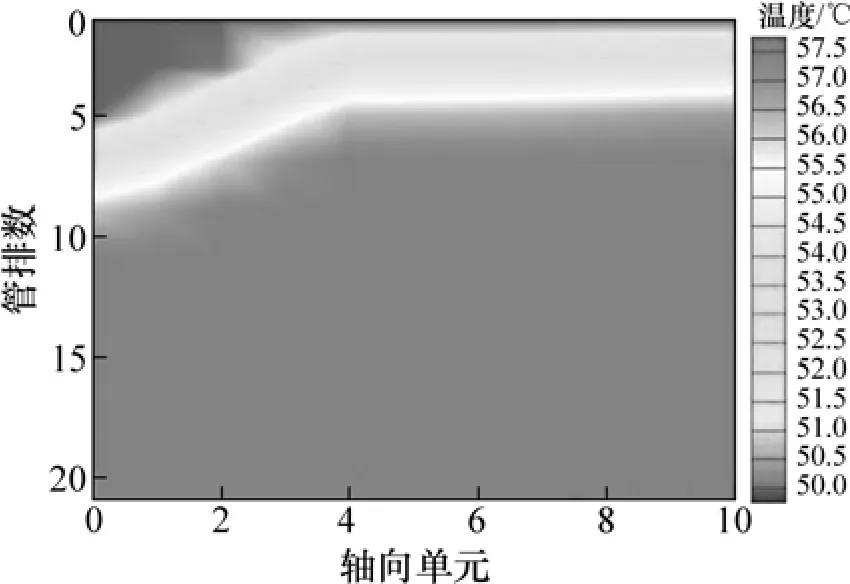
图6 海水温度场分布Fig.6 Distribution of seawater temperature field
4.4 传热特征
蒸发器内部的传热特征如图7~9所示。由图7可知:蒸汽进入管束后沿管长方向逐渐冷凝,通过释放潜热将热量传给管外海水,干度也逐渐降低且变化较为平稳,说明蒸汽沿管长流动过程中并未出现急剧冷凝现象,整体传热状况良好。在1管程出口处平均干度约为0.15,剩余蒸汽经管箱折返后进入2管程直至完全冷凝。另外,总传热系数也可以表征各个计算单元的换热效果,与管内、外传热系数密切相关,特别受蒸汽质量流速、干度以及海水喷淋密度影响较大。由图8和图9可知:在1管程和2管程蒸汽进口处总传热系数最大,约为3.3 kW/(m2K),而后沿管长方向逐渐减小,说明进口区换热较强,特别是2管程表现得更加明显,因为该区域蒸汽干度大,管内扰动强烈,使得管内传热系数较大;而后沿管长方向冷凝换热逐渐减弱,总传热系数也发生较大变化,管内单相流动时总传热系数很小,仅相当于管内蒸汽冷凝情况下总传热系数的7%左右。在1管程进口的下半区总传热系数略有减小,原因在于上半区海水已经达到饱和状态,开始蒸发汽化,喷淋密度沿管排方向逐渐减小,管外液膜波动减缓,削弱了管外换热,进而影响了总体传热。此外,整个蒸发器总传热系数的平均值为2.8 kW/(m2K),已经达到了设计参数要求。
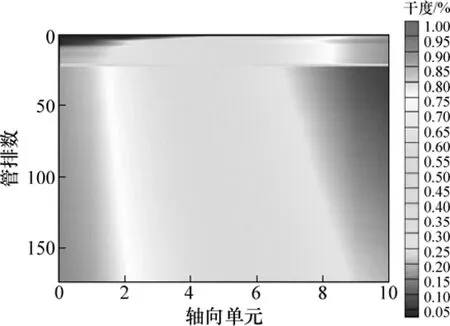
图7 蒸汽干度分布Fig.7 Distributions of steam quality

图8 2管程总传热系数分布Fig.8 Distributions of overall heat transfer coefficient for second tube pass
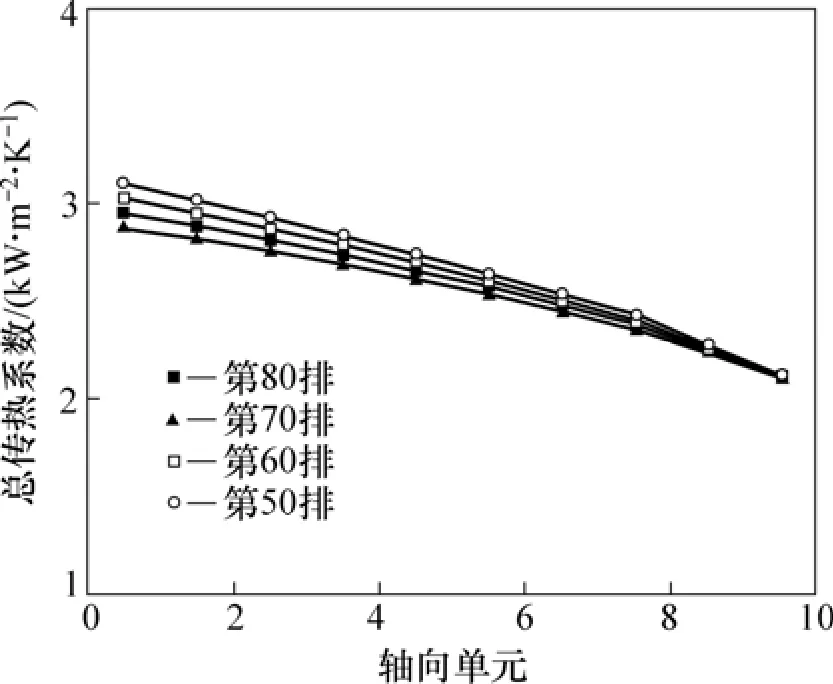
图9 1管程总传热系数分布Fig.9 Distributions of overall heat transfer coefficient for first tube pass
4.5 海水盐度分布
蒸发器内海水盐度的变化情况如图10所示。与图4所表述的流场分布一一对应,表现出“上小下大”的趋势。由于2管程海水的喷淋密度基本保持不变,其盐度也维持在36 g/kg。当海水到达1管程后开始蒸发,产生二次蒸汽,喷淋密度逐渐减小,盐度则随之升高。在1管程中部海水盐度整体变化较为平稳,从36 g/kg逐渐增加到48 g/kg。在1管程进口的下半区海水盐度明显升高,最大值达到56 g/kg,再次说明此区域换热强烈,生成较多的二次蒸汽。但是海水盐度过高,会促使其在蒸发过程中所含盐分受热分解并转化成不同形态物质沉淀在传热管表面形成结垢,因此在工程设计中应当格外引起注意,控制海水浓缩比不超过2.5,最高温度低于70 ℃可以避免发生上述现象。

图10 海水盐度分布Fig.10 Distributions of seawater salinity
5 结论
(1) 建立了水平管降膜蒸发器实体的三维分布参数模型,数值解与实际值的相对误差在-4.2%~1.6%范围内,验证了该模型的可靠性,该模型适用于单元复叠循环计算且成本低廉。
(2) 通过模拟蒸发器内部的热力过程,获得了大量流场、温度场和传热参数分布信息,真实地反映了蒸发器内部复杂的流动与传热特性,以细观角度揭示出局部区域流体流动和传热的深层次问题。
(3) 三维分布参数模型是进行水平管降膜蒸发器数值研究的一种合理且实用的模型,对蒸发器的机理研究及整体的优化设计具有指导意义。
[1]周赤忠,李焱. 当前海水淡化主流技术的分析与比较[J]. 电站辅机,2008,29(4) : 1-5.ZHOU Chi-zhong,LI Yan. Analysis and comparison between current major technologies of seawater desalination[J]. Power Station Auxiliary Equipment,2008,29(4): 1-5.
[2]宿翠霞,倪华秋,李凌霄,等. 海水淡化技术及其应用现状[J].中国资源综合利用,2009,27(7) : 31-32.SU Cui-xia,NI Hua-qiu,LI Ling-xiao,et al. Seawater desalination technology and its application[J]. China Resources Comprehensive Utilization,2009,27(7): 31-32.
[3]Alasfour F N,Darwish M A,Bin Amer A O. Thermal analysis of ME-TVC+MEE desalination systems[J]. Desalination,2005,174(1): 39-61.
[4]Darwish M A,El-Dessouky H. The heat recovery thermal vapor-compression desalting system: A comparison with other thermal desalination processes[J]. Applied Thermal Engineering,1996,16(6): 523-537.
[5]Dey P K,Hawlader M N A,Chou S K,et al. Performance of a single-effect desalination system operating with different tube profiles and materials[J]. Desalination,2004,166(15): 69-78.
[6]Zhang L N,Yang C X,Zhou J H. A distributed parameter model and its application in optimizing the plate-fin heat exchanger based on the minimum entropy generation[J]. International Journal of Thermal Sciences,2010,49(8): 1427-1436.
[7]Rodriguez M,Diaz M S. Dynamic modeling and optimisation of cryogenic systems[J]. Applied Thermal Engineering,2007,27(7):1182-1190.
[8]Wang F Q,Maidment J F,Missenden J F,et al. A novel special distributed method for dynamic refrigeration system simulation[J]. International Journal of Refrigeration,2007,30(5):887-903.
[9]Sultana P,Wijeysundera N E,Ho J C,et al. Modeling of horizontal tube-bundle absorbers of absorption cooling system[J].International Journal of Refrigeration,2007,30(4): 709-723.
[10]Zavala-Rio A,Santiesteban-Cos R. Reliable compartmental models for double-pipe heat exchangers: An analytical study[J].Applied Mathematical Modelling,2007,31(9): 1739-1752.
[11]Chato J C. Laminar condensation inside horizontal and inclined tubes[J]. American Society of Heating Refrigerating and Airconditioning Engineers Journal,1962,4: 52-60.
[12]Jaster H,Kosky P G. Condensation heat transfer in a mixed flow regime[J]. International Journal of Heat and Mass Transfer,1976,19(1): 95-99.
[13]杨世铭,陶文铨. 传热学[M]. 北京: 高等教育出版社,1998:168-169.YANG Shi-ming,TAO Wen-quan. Heat transfer[M]. Beijing:Higher Education Press,1998: 168-169.
[14]Sernas V. Heat transfer correlation for subcooled water films on horizontal tubes[J]. Transactions of the ASME,1979,101(1):176-178.
[15]Parken W H,Fletcher L S,Sernas V,et al. Heat transfer through falling-film evaporation and boiling on horizontal tubes[J].Journal of Heat Transfer,1990,112(3): 744-750.
[16]Ould Didi M B,Kattan N,Thome J R. Prediction of two-phase pressure gradients of refrigerants in horizontal tubes[J].International Journal of Refrigeration,2002,25(7): 935-947.
