非结构化环境下自主车辆轨迹规划方法

陈清阳，张小波，孙振平，贺汉根

(国防科学技术大学 机电工程与自动化学院，湖南 长沙，410073)

在当今信息化社会，作为一个国家自动化和智能化水平高低的典型代表，自主驾驶车辆的研究受到了前所未有的关注，许多发达国家如美国和德国等，都投入了大量的人力物力进行研究[1-3]，但是到目前为止相关的研究仍不能很好地解决非结构化环境下车辆的自主导航。而轨迹规划作为其中的关键部分，更是存在着许多问题有待解决[4-6]。面向非结构化环境，最主要的特点便是环境的复杂性及广泛存在的不确定性。无论是感知系统，还是定位系统，都无法为轨迹规划提供准确的信息。可能存在的动态障碍物，对轨迹规划也提出了巨大的挑战。另一方面，面向实际车辆自主驾驶的轨迹规划方法，运动动力学约束与实时性之间的矛盾更是制约着车辆智能驾驶系统的发展。尽管目前人们对这一难题进行了很多研究，提出了许多有创意的想法，如在加速度空间对机器人运动进行避障与目标跟踪规划[7]，Qu等[8-11]所提出的多项式等数值解析方法，改进的 A*搜索算法[12]及 Bottasso等[13-14]所提出的轨迹原子方法，Flores等[15]所提出的微分平坦等，这些方法都对移动机器人的运动规划研究起了巨大的推动作用，但是面对实际车辆运动过程，实时性仍是一个难以解决的问题。本文作者对非结构化环境下的自主驾驶车辆轨迹规划问题提出了一种融合车辆运动特性的轨迹规划方法。本文将实现一种两点约束下的可行轨迹生成方法，仿真结果显示该方法得到的轨迹具有光滑的曲率特性，符合车辆实际运动特性；在此基础上，本文作者将基于实际车辆自主驾驶中初始状态、目标状态及障碍物约束，实现基本可行的初始轨迹系列；最后，基于本文所提出的优化指标对轨迹系列进行评价，得到一条适合车辆运动的期望轨迹。

1 两点约束下可行轨迹生成方法

首先介绍本文主要采用的两点约束下可行轨迹生成方法。对问题进行建模，如图1所示，在参考坐标系XOY中，为简化问题表示，假设初始状态即位于O点，目标状态位于O′(否则可通过一定的平移与旋转操作实现)。针对本文要研究的自主车辆轨迹规划问题，O点的状态表示为O(0,0,90)，其中，90代表此参考坐标系下车辆航向与横轴的夹角，O′点的状态表示为O′ (x,y,α)，α代表此坐标系下目标点方向与横轴的夹角，算法将解决初始状态O与目标状态O′约束下可行轨迹的实现。

图1 两点约束建模表示Fig.1 Model of two-point constraints

基本思想：由几何知识可知，基于一段固定曲率的圆弧同时满足初始状态与目标状态约束，在大部分情况下是不可能实现的。因此，本文采用一种渐近逼近的算法，实现基本满足这两点约束的可行解。首先，本文将目标状态的约束弱化为O″(x,y)，由几何知识可知，由一段光滑的圆弧可同时满足初始状态与弱化目标状态的约束条件，具体见式(1)～(3)(在这里只列举目标点位于第一象限的情况，其他状态可类比得到)。

式中：β为OO′连线与横轴的夹角；lOO′为OO′连线的距离；(xc,yc)为圆弧上的一个采样点c的坐标；θc为采样点与横轴的夹角。

同样的，在目标状态与弱化的初始状态约束下，依据上述方法可得到一段固定曲率的圆弧。在2段圆弧上均匀采样，可得到相应的点对(xc,yc)与(xc′,yc′)，基于式(4)可实现2段圆弧的渐近过渡。

实验中取ε= 1-i/M，η=i/M，i为圆弧上的采样点序号，M为采样点个数，算法得到的仿真结果如图2所示。图2(a)中轨迹1为基于初始状态与弱化目标状态所得到的可行轨迹，轨迹2为基于目标状态与弱化初始状态所得到的可行轨迹，而图中的合成轨迹则是基于式(4)所得到的渐近过渡轨迹。由图2(b)中相应的合成轨迹曲率可以看到，得到的合成轨迹具有光滑的曲率特性，符合实际车辆的运动特性。

2 初始轨迹系列生成方法

在前一部分讨论了两点约束下车辆可行轨迹的生成方法。在此基础上，将面向实际非结构化环境下车辆自主导航的需求，提出满足实时性要求的轨迹规划方法。首先本文作者将在前述算法的基础上，在初始状态与目标状态及障碍物约束下实现基本可行的初始轨迹系列。

2.1 初始状态与目标状态约束

基于初始状态与目标状态对轨迹进行约束，首先要实现的是规划坐标系的建立及车辆状态与目标状态在规划坐标系中的投影。为了实现对障碍物的准确表示，本文将建立图3所示的规划参考坐标系XVY，图3中车辆位于坐标系原点V，而目标状态经过一定的平移与旋转操作位于Y轴上的某一点。如此的坐标系表示方法，可更准确地实现障碍物的膨胀表示与车辆在规划坐标下的质点表示。在图3中，规划坐标系下的车辆方位角如图中V点处箭头所示方向，目标方向则为T点处箭头所示方向，图3中黑色块状区域表示的是车上所装传感器实际感知到的不可通行区域。下面将讨论本文所介绍的方法在实际车辆导航中的应用。在图3(a)中，由车辆所在位置V及车辆方向角(即为图3中V处箭头所指方向)，结合弱化的目标状态约束T，即目标点T的位置，可得到固定曲率的圆弧轨迹1，即；类似地，由完整的目标状态T及弱化初始状态约束，即V的位置，可得到固定曲率的圆弧轨迹2，即。在此基础上，基于前面所介绍的两段圆弧渐近过渡的方法，可实现可行的初始轨迹，即为图3中合成轨迹所代表的曲线。由图3中合成轨迹的曲率图可以看到，合成轨迹的曲率光滑过渡，适合于实际的车辆控制。

图2 两点约束下轨迹生成算法仿真结果Fig.2 Simulation results of proposed algorithm under two-point constraints

2.2 障碍物约束

由前面所提到的方法获得的基于初始状态及目标状态约束的基本可行轨迹，在某些情况下并非是安全可行的。图4所示为实车实验过程中遇到的一帧规划。此时图中可行的合成轨迹明显与黑色不可通行区域发生重叠，因此，所得到的合成轨迹实际上是不可行的。如何在前述方法的基础上满足障碍约束，这便是本节要解决的问题。

借鉴前面所介绍的两点约束下可行轨迹生成算法，本文将采用一种多分辨率细分的方法来解决轨迹的避障问题。沿用图4所示的场景，假设在当前实现的基本可行轨迹上第k个路径点与障碍物发生碰撞，则在第k点的基础上按式(5)进行相应的平移变换操作，可获得一系列不与障碍相碰的候选局部目标点k1,k2,k3,…,kn。

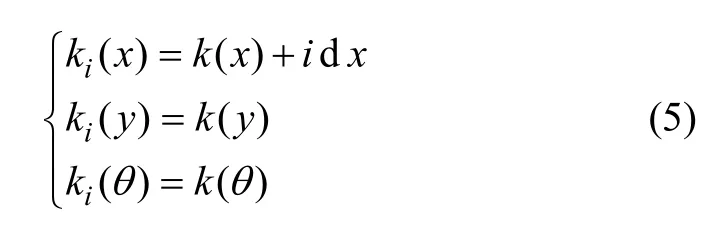
在一系列候选目标点的基础上，同样地，依据两点约束下可行轨迹生成方法，可分别获得由初始状态及候选局部目标状态约束的可行轨迹及候选目标状态与目标状态约束的可行轨迹。由于在候选局部目标点处同时考虑了该点的方向属性，因此，由与连接而成的曲线也是一条可行的规划轨迹，具体实验结果如图5(a)中的点所代表的系列曲线。由图5(b)可以看到：得到的合成轨迹曲率与图4中合成轨迹曲率相比，尽管具有较大的跳变，但是仍是平滑过渡的，对于实际车辆的控制意味着以较低的速度行驶，这与原始障碍图中的场景是相一致的。

可得到不与障碍物发生重叠的轨迹系列，因此，轨迹仍保持相对平滑的过渡特性。在得到的一系列基本可行轨迹的基础上，基于一定的优化目标对轨迹系列进行评价，得到此优化指标下的最优可行轨迹。

图3 本文所建立的规划坐标系及初始状态与目标状态约束下得到的结果Fig.3 Representation of proposed planning frame and results under constraint of initial-final state

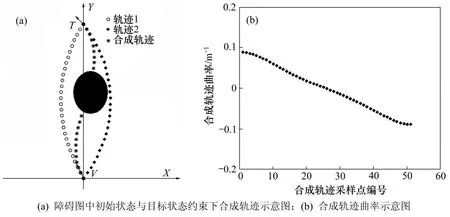
图4 实车实验中遇到的一帧规划曲线Fig.4 Example in real vehicle experiments

图5 障碍约束下系列轨迹生成结果Fig.5 Series of trajectories generation with obstacle constraints

3 最优可行轨迹

在前文中详细讨论了基本可行轨迹系列的实现，在此轨迹系列的基础上，将基于一定的优化指标对轨迹系列进行评价，得到最优的可行轨迹，保证车辆以较高的速度安全行驶。

首先，对于自主车辆的运动，安全性是第一位的。对于轨迹规划来说，这要求规划的轨迹在保证可行性的基础上必须离障碍物足够远，以避免由于感知、规划及控制等环节所存在的误差带来的潜在危险性。在前面介绍的轨迹系列的基础上，对于某一轨迹上的采样点p(x,y)，在感知地图内对其邻近区域Q(p(x,y),D)(以p(x,y)为圆心，以D为半径的圆区域)进行障碍相关性判断。若是在Q(p(x,y),D)区域内与障碍在距离d处相交，则可得到该点的安全距离d(x,y)，否则，其安全距离便为D。在此基础上，定义轨迹的安全指标为：

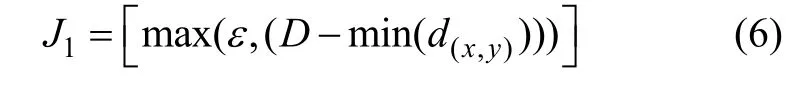
需要指出的是：式(6)中的D为由于感知、规划、控制等各方面的误差所期望的最小安全距离，min(d(x,y))为某一规划轨迹上所有采样点的最小安全距离，ε为大于0的较小实数，代表在期望安全距离之外的规划轨迹，行车安全代价为可以接受的较小值。对于该安全指标，最优轨迹为轨迹系列中对应于minJ1的可行轨迹。

在保证安全可行的基础上，基于规划轨迹实现车辆控制自然是期望车辆能以较高的速度行驶。对于实际车辆来说，由于受到各种极限物理条件的限制，制约了车辆沿着规划轨迹行驶所允许的最高速度。由式(7)可知：在固定的转弯半径，即曲线曲率的基础上，车辆的行驶速度必须满足最大侧向加速度约束，否则车辆的侧向摩擦力不足以提供车辆转弯所必需的向心力，可能产生打滑等现象，这对于车辆的运动控制来说是非常不利的。

式中：v为车辆速度；r为轨迹的相应曲率；amax为实际车辆运动允许的最大侧向加速度；rmin为由于车辆的物理条件所允许的最小转弯半径。

因此，为了提高车辆的行驶速度，本文定义轨迹的效能指标为：

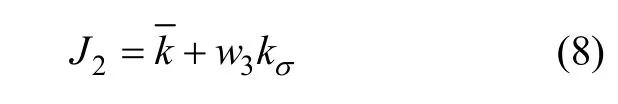
式中：为某一规划轨迹上的曲率均值；kσ为规划轨迹的曲率方差；w3为协调两者之间关系的权值。该指标在考虑规划轨迹的平均曲率的基础上，同时对曲率方差进行约束，保证完整轨迹的光滑特性，较好地体现了车辆行驶快速性对规划轨迹的约束。基于该指标的最优轨迹即为轨迹系列中实现 m inJ2的相应轨迹。在该指标的基础上，为了满足实际车辆的物理限制，必须满足式(9)中的条件。

式中：φ为车辆前轮摆角；φ为前轮摆角转速。

结合前面的讨论，面向实际自主车辆的运动，本文给出了如下的优化指标：

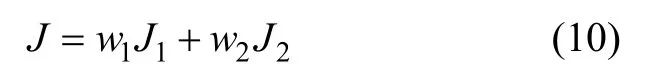
其中：w1和w2为对应安全性与效能指标的权值系数，实现两者之间较好地折中，保证在各种情况下都能得到最优的轨迹。

4 实验结果

基于本文所提出的融合车辆运动特性的轨迹规划方法，作者进行了大量的实车实验，实验面向的主要是复杂非结构化环境，部分实验场地与实验结果如图6所示。在实验结果中白色的块状区域表示检测到的障碍物，白色点所代表的曲线则为实际规划的轨迹。在该规划结果的指引下，实验车辆可较好地完成轨迹跟踪与安全避障任务，峰值速度可接近 30 km/h。更主要的是，在实际测试过程中，轨迹规划周期在 100 ms以内，满足实际车辆自主驾驶的需求，对于智能驾驶技术的实际应用具有巨大的推动作用。

图6 实车实验环境与实验结果Fig.6 Experimental environments and results

5 结论

(1) 针对非结构化环境下自主车辆轨迹规划问题，首先提出一种两点约束下可行轨迹生成算法。该算法得到的轨迹具有光滑的曲率特性，符合车辆实际运动特性。在此基础上，综合考虑车辆初始状态、目标状态及障碍物约束，实现基本可行的初始轨迹系列。最后为了保证自主车辆安全与快速地运动，提出合理的优化指标，对轨迹系列进行评价，从而得到期望的理想轨迹用于车辆控制。

(2) 实验表明，该方法满足车辆自主导航的实时性需求，同时考虑了车辆运动特性，在非结构化环境下能较好地实现轨迹跟踪与避障等功能，适合复杂环境下智能车辆自主导航应用。

[1]Montemerlo M,Becker J,Shat S,et al. Junior: The stanford entry in the urban challenge[J]. Journal of Field Robotics,2008,25(9): 569-597.

[2]Kammel S,Ziegler J,Pitzer B,et al. Team AnnieWAY’s autonomous system for the 2007 DARPA Urban Challenge[J].Journal of Field Robotics,2008,25(9): 615-639.

[3]Bacha A,Bauman C,Faruque R,et al. Odin: Team VictorTango’s entry in the DARPA Urban Challenge[J]. Journal of Field Robotics,2008,25(8): 467-492.

[4]蔡自兴,贺汉根,陈虹. 未知环境中移动机器人导航控制研究的若干问题[J]. 控制与决策,2002,17(4): 385-390.CAI Zi-xing,HE Han-gen,CHEN Hong. Some issues for mobile robots navigation under unknown environments[J]. Control and Decision,2002,17(4): 385-390.

[5]John J L. Challenges for autonomous mobile robots[C]//Proceedings of International Machine Vision and Image Processing Conference. Maynooth: Inst of Elec and Elec Eng Computer Society,2007: 4.

[6]蔡自兴,贺汉根,陈虹. 未知环境中移动机器人导航控制理论与方法[M]. 北京: 科学出版社,2009: 1-7.CAI Zi-xing,HE Han-gen,CHEN Hong. Theory and methods for mobile robots navigation under unknown environments[M].Beijing: Science Press,2009: 1-7.

[7]ZU Di,HAN Jian-da,TAN Da-long. Acceleration space LP for the path planning of dynamic target pursuit and obstacle avoidance[C]//Proceedings of the World Congress on Intelligent Control and Automation (WCICA). Dalian: Institute of Electrical and Electronics Engineers Inc,2006: 9084-9088.

[8]QU Zhi-hua,WANG Jing,Plaisted C E. A new analytical solution to mobile robot trajectory generation in the presence of moving obstacles[J]. IEEE Transactions on Robotics,2004,20(6): 978-993.

[9]Park S H,Lee B H. A new analytical representation to robot path generation with collision avoidance through the use of the collision map[J]. International Journal of Control,Automation and Systems,2006,4(1): 77-86.

[10]Nagy B,Kelly A. Trajectory Generation for Car-like Robots using Cubic Curvature Polynomials[C]//Proceedings of International Conference on Field and Service Robotics. Helsinki,2001: 731-736.

[11]Thompson S,Kagami S. Continuous curvature trajectory generation with obstacle avoidance for car-like robots[C]//Proceedings of International Conference on Computational Intelligence for Modelling,Control and Automation,and International Conference on Intelligent Agents,Web Technologies and Internet. Vienna: Inst of Elec and Elec Eng Computer Society,2005: 863-870.

[12]Likhachev M,Ferguson D. Planning long dynamically feasible maneuvers for autonomous vehicles[J]. International Journal of Robotics Research,2009,28(8): 933-945.

[13]Bottasso C L,Leonello D,Savini B. Path planning for autonomous vehicles by trajectory smoothing using motion primitives[J]. IEEE Transactions on Control Systems Technology,2008,16(6): 1152-1168.

[14]陈杨. 基于轨迹片段的运动规划方法及其在自主车辆中的应用[D]. 长沙: 国防科学技术大学研究生院,2006: 11-24.CHEN Yang. Motion planning method based on trajectory primitives and its applications in autonomous land vehicles[D]. Changsha: National University of Defense Technology. Graduate School,2006: 11-24.

[15]Flores M E,Milam M B. Trajectory generation for differentially flat systems via NURBS basis functions with obstacle avoidance[C]//Proceedings of the American Control Conference.Minneapolis: Institute of Electrical and Electronics Engineers Inc,2006: 5769-5775.