基于多模型集成的铁矿粉库存量预测方法

蔡雁，吴敏，王绍丽，王春生

(中南大学 信息科学与工程学院，湖南 长沙，410083)

钢铁企业的采购物流成本占企业总成本的60%～70%，并且随着世界经济发展，各个钢铁企业对于原材料的需求日益增加，企业出现原料存放场地不足、资金紧张等问题[1]。这时，通过准确预测原材料库存量，制定合理的采购计划是节约企业成本的关键。通过对钢铁企业铁矿粉库存量的准确预测，根据预测结果制定合理的采购计划，可以防止因采购量过大导致库存积压引起的成本制约和采购量过小引起的异常生产。目前国内外钢铁企业主要采用扩大料场规模及合理安排料场原料存放位置等方法来增加原材料库存储量[2-4]，而一些矿产公司则采用全流程跟踪矿粉供应链的方法实现企业库存量的实时监控[5]。钢铁企业为满足生产需求，通过扩大原料存储场地面积，从新布局堆位的方法来实现，但这种方式耗费较大资金，不能从根本上优化企业采购成本。通过对库存量进行准确预测，然后制定合理采购计划，这是解决原料供应优化问题的重要途径。从理论上说，钢铁企业铁矿粉的库存量主要由每天或每批次的生产计划和采购计划决定，但是在实际生产中，铁矿粉库存量受到采购瓶颈，季节型订单或订单波动，物料损失等外在因素的影响，存在较多的不确定性因素。这些不确定因素较难预测，而且其对库存量的影响也较难定量描述。本文作者考虑到不确定因素对库存量的影响实际上反映在库存量的时间序列数据中，通过对时间序列数据的有效分析与建模，可以真实反映库存量影响的主要因素及影响因子较小的不确定性因素。根据以上库存量预测特点，本文作者提出一种基于灰色系统模型与时间序列模型集成的预测方法来预测铁矿粉库存量。首先利用灰色系统可以反映数据序列整体发展趋势的优点，通过对库存量历史数据的滤波、统计、累加或累减生成，建立库存量灰色预测模型，然后利用时间序列模型可以反映数据序列细节波动的优点，通过数据序列进行时序分析，建立时间序列自回归积分移动平均模型；最后，建立基于信息熵的铁矿粉库存量集成预测模型，集成可以充分集合不同类型模型的优点，准确预测铁矿粉库存量。

1 原料场工艺及其特性分析

钢铁企业原料场工艺流程如图1所示。

原料场铁矿粉原料分为火车来料和汽车来料，也可分为国内矿粉与国外矿粉。影响各种矿粉库存量的首要因素为来料量。原料到达原料场后经由传送带进行大块筛分，筛分后用堆料机将铁矿粉堆至一次料场，形成实际的铁矿粉料堆，铁矿粉料堆经过堆取料机与相关皮带放置原料场的多个预配料仓中称为上料，上料过程是预配料的前提。原料场存放的铁矿粉原料一部分经过堆取料机与传送带直接送至高炉称为高炉用料。经过预配料过程形成中和粉，将混合后的中和粉经传送带与堆取料机根据一定的规则放置二次料场称为混匀堆料，混匀堆料环节完成后会在二次料场形成实际的中和粉料堆。在原料场物料被不断传送的过程中，有多种因素会引起物料库存量的变化。

(1) 在大块筛分环节汽车运走的大块料不计量导致少量物料流失，使个别矿粉的实际库存量偏低。在物料堆放至一次料场过程中由于洒料等因素会有少量的物料流失。

(2) 上料过程因天气影响，存在传送带或预配料仓粘料而导致物料流失的情况。

图1 原料场工艺流程Fig.1 Process of raw material plant

(3) 混匀堆料过程物料计算精度较高，物料流失可忽略。

(4) 物料在一次料场存放过程中消耗时间长短不同，某些物料会因堆放时间过长而导致料堆下限，使实际的库存量偏高。

从原料场工艺可以看出：铁矿粉库存量受到设备、天气等因素的干扰，且干扰因素影响库存量的具体值较难统计，而这些干扰因素可以间接体现在库存量的统计结果中。因此，本文采用针对结果建模的方法对库存量进行预测，以克服众多干扰因素对库存量影响难于估计的局限性。

2 基于残差修正的等维新息GM(1,1)库存量预测模型

铁矿粉库存量不仅受到企业采购计划及生产计划的影响，且受到各种外在因素，如订单的突然增加或减小、采购瓶颈、季节性的交通瓶颈等问题的影响，不仅具有白信息覆盖，同时具有较大的灰信息覆盖。

2.1 灰色系统建模思想

灰色系统的基本思想是：使系统从结构上、模型上、关系上由灰变白或增加白度，从对灰色信息的认知不多到知之较多，从而认知其中隐藏的变化规律[6]。灰色系统的思想适用于铁矿粉库存量预测，并且由于灰色模型对变化缓慢的序列及波动范围有限的时间序列有良好的预测效果。由于钢铁企业原料场生产要求原料供应充分且准时化，外在影响因素不允许导致库存量大范围波动，故采用灰色模型进行预测是合适的。

2.2 库存量预测GM(1,1)模型

取库存量最新的6个历史数据构成原始序列X(0)：

式中：n=6。

首先，对库存量原始序列(0)X进行一次累加生成，得到：

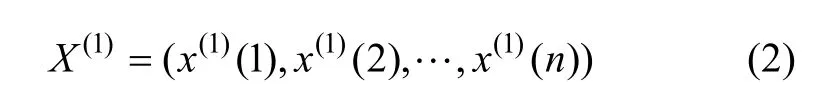
然后，构造背景值序列：

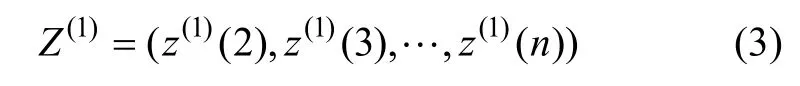
采用一次累加后序列，建立灰色GM(1,1)模型的白化微分方程，即：

式中：a为发展系数，反映序列库存量数据序列的增长速度；b为灰色作用量。

利用最小二乘估计求得估计参数列[a,b]T：

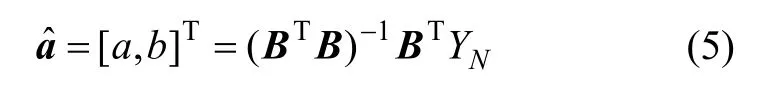
式中：

根据式(5)即可求出参数a和b值。

根据选取的库存量原始数据序列，得到库存量预测值为：

残差修正灰色预测模型是将残差预测值加到原预测值上，以补偿原预测值，达到提高精度的目的[7]。原数据序列与预测数据序列之差为残差序列：

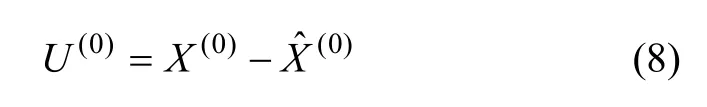
对残差序列建立GM(1,1)模型，解为：

式中：a′为发展系数，反映库存量预测残差序列的增长速度；b′为残差预测模型灰色作用量。

将式(6)与式(10)相加得残差修正预测模型的预测结果为：

随着时间的推移，一些干扰因素不断的进入系统并产生影响。为了将库存量新的影响因素考虑进去，GM(1,1)模型将每一个新的库存量数据送入到原始序列中，重新建立模型，即形成库存量预测等维新息GM(1,1)模型。在加入新数据并去掉老数据后，再重复GM(1,1)的建模步骤，得到的预测公式会随着新数据序列而发生改变，使模型更好的适应当前状态[8]。由于GM(1,1)模型描述的是系统的一阶特性，因此，对变化缓慢的序列具有较高的预测精度，适用于长期静态预测。然而，外在影响变化较大时，或系统的高阶信息对输出的影响不能忽略时，其预测精度下降，因此，本文引入自回归积分移动平均ARIMA模型，以描述系统的动态特性与高阶特性。

3 库存量预测ARMA模型

铁矿粉库存量观测值之间有一定的依赖性和相关性，时间序列预测认为：通过分析历史时间序列，根据时间序列所反映出来的发展过程、方向和趋势，进行类推或延伸，可以预测下一段时间达到的水平。预测模型属于动态模型，适合于具有动态变化规律的数据，适合做短期预测，与灰色系统理论能够预测缓慢变化数据的特点能够互相补充。因此，本文采用灰色预测与时间序列预测结合的方式能够全面反映库存量变化特点。

3.1 ARMA模型选择

自回归移动平均 ARMA模型是一种精度较高的时间序列短期预测模型，广泛应用于各种类型时间序列数据的预测与分析[9]。基本思想是：某些时间序列是依赖时间t的一族随机变量，构成该时间序列的单个序列虽然具有不确定性，但整个序列的变化却有一定的规律性，可以用相应的数学模型加以描述。通过对该数学模型的分析研究，能够更本质的认识时间序列的结构与特征，达到最小方差意义下的预测[10]。

在本文对于铁矿粉库存量数据进行时序分析过程中，根据原料场物料系统特点，可以从不同类型的ARMA时序模型中选择合适的模型类型，比较典型的ARMA模型有自回归模型AR(p)，将当前值描述为自身过去p个观测值的线性组合；移动平均模型MA(q)，将当前值描述为过去q个时期预测误差的线性组合；ARMA(p,q)是由AR(p)与MA(q)组合构成，以上几类模型适合于描述平稳时间序列，而对于非平稳时间序列，只要通过适当阶的差分运算就可以实现平稳[11]。差分后的模型称为ARIMA(p,d,q)模型，其中d为差分的阶数，所以，在构建库存量预测模型时，根据库存量数据原始序列特点，在数据分析基础上，本文选择ARIMA(p,d,q)类型的时序模型进行库存量预测模型的构建。

3.2 库存量预测ARIMA(p,d,q)模型

ARIMA(p,d,q)模型的构建首先要进行模型结构和阶次的辨识。本文将铁矿粉库存量历史数据作为时间序列数据，统计数据以天计算，以某钢铁厂单种高品位铁矿粉库存量预测为例进行模型的构建，取2009年10月～2010年1月的100个原始动态库存量数据构成原始序列{xt}，首先进行 Augmented Dickey-Fuller test (ADF test,也称ADF单位根检验)，判断原始序列是否为平稳序列，否则进行差分处理，直至通过ADF单位根检验，此时差分阶数即为ARIMA(p,d,q)模型阶数，即d。验证过程利用Eviews 5.0[12]仿真软件包实现，具体结果如表1和表2所示。

表1和表2中，|t统计值|＜|τ临界值|，即|t统计值|=2.80＜|τ0.05|＜|τ0.01|，很明显原始序列没有通过单位根检验；在线性回归方程显著性检验中，在一定显著性水平下，若检验统计值大于临界值，则回归方程显著。但是，有可能出现原假设是对的却被拒绝的情况，即“弃真”的错误，在模型检验中，允许犯这类错误的概率，称为相伴概率P。在仿真分析时，Eviews求解出“弃真”的概率P，若P小于置信度，即认为方程显著性明显，否则说明方程显著性不明显，本文将置信度设为0.05，从表1可以看出，P=0.061 5，说明方程显著性不明显。

通过t统计值与P值检验，表明数据序列{xt}为非平稳序列，要进行差分处理。

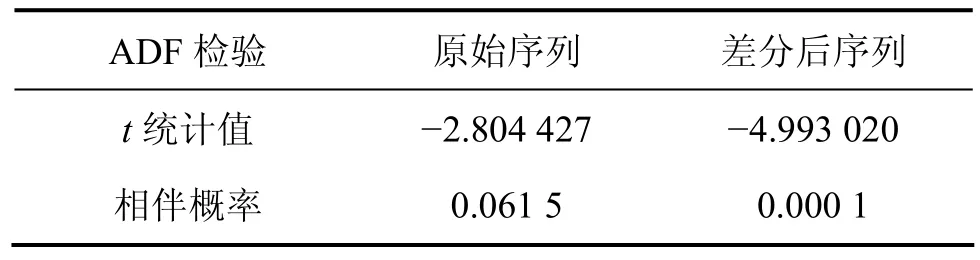
表1 ADF单位根检验Table 1 ADF unit root test

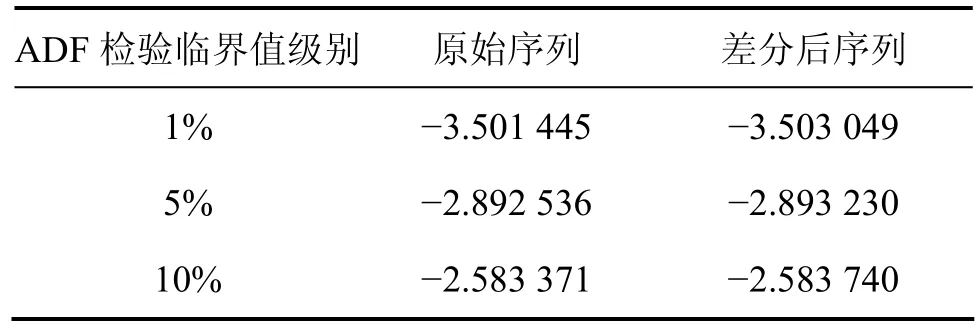
表2 检验临界值Table 2 Check critical value

差分处理将原始序列变换为平稳序列后，要进行模型的识别和定阶，即确定模型中p与q，模型的定阶要通过计算样本序列{zt}的自相关函数Autocorrelation Function (简称 ACF)与偏自相关函数Partial Autocorrelation Function(简称PACF)，自相关函数是描述随机信号zt在任意2个不同时刻取值之间的相关程度，偏自相关函数为消除噪声影响下，随机信号zt是2个不同时刻取值之间的相关程度。{zt}的ACF值ρk的求解式为：

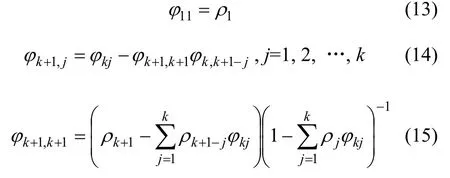
采用Eviews工具，计算结果见图2。

图2 差分后序列的自相关-偏自相关函数Fig.2 ACF-PACF functions of differential time series

在图2中，Autocorrelation为自相关函数ACF，Partial Correlation为偏自相关函数PACF。根据模型差分阶次及图2中模型的ACF和PACF的滞后阶数，模型可能存在多种结构，此时需要使用赤池信息量准则(Akaike Infromation criterion，简称AIC)和西沃兹信息准则(Schwarz Criterion，简称 SC)准则对模型进行比较，在统计学中，建立的多个时间序列模型中，使AIC和SC函数值达到最小的模型为相对最优模型[13]，比较结果如表3所示。

模型结构的判定准则见表 4，根据模型的判定准则与ACF和PACF的计算结果可以看出：自相关系数ACF在滞后阶数为4时显著不为0，即p=4，偏自相关函数PACF在滞后阶数为1时显著不为0，即q=1。

由表3可以看出：当p=4，d=1，q=1时，模型结果 AIC与 SC值达到最小，模型最优，根据分析结果可得出针对该种铁矿粉库存量数据序列可建立ARIMA(4,1,1)模型。模型结构确定后判断模型是否适用需要进行模型的检验，对于ARIMA(p,d,q)模型结果的检验采用诊断残差序列{εt}是否服从白噪声分布的方法，残差样本序列n为100，最大滞后期可取n/10或，通过 Eviews计算样本残差序列的 ACF与PACF。具体结果如图3所示。

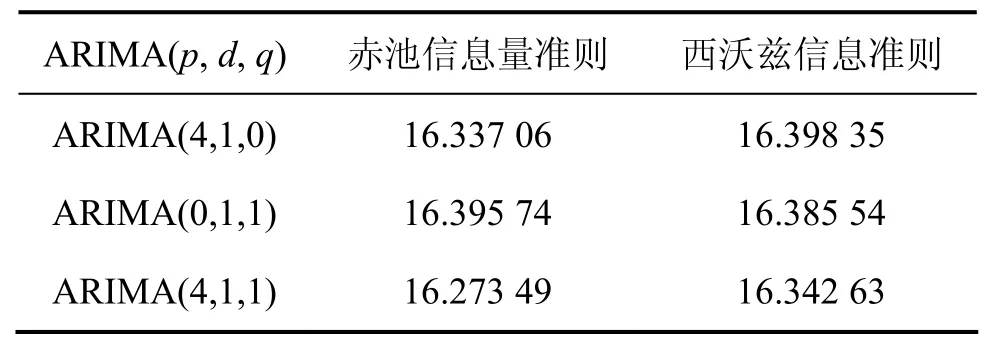
表3 多个ARIMA模型AIC与SC比较Table 3 Comparison of AIC and SC for more ARIMA models

表4 ARMA(p,q)模型结构识别准则[14]Table 4 ARMA(p,q) model structure identification principle[14]

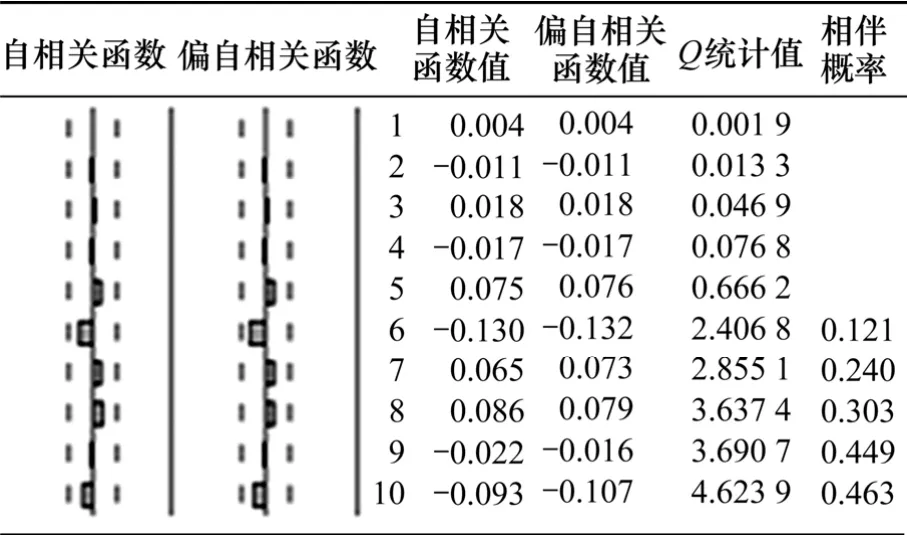
图3 残差的自相关-偏自相关函数Fig.3 ACF-PACF functions of residuals

从图3可以看出：当滞后期小于10时，残差序列的自相关系数都落入随机区间，表明残差序列是纯随机的，即残差序列通过白噪声检验。因而，对该种铁矿粉序列建立ARIMA(4,1,1)模型是合理的，序列{zt}的最终ARIMA(4,1,1)模型为：

其中：B为时间滞后算子；εt为t时刻预测模型残差，

式(16)经过微分转化后，得到时间序列预测模型：

对{zt}进行一阶反差分可得原始序列{xt}的时间序列模型为：

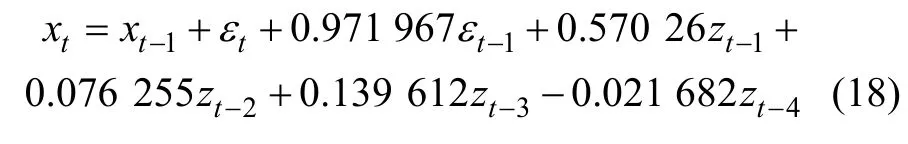
ARIMA(4,1,1)辨识出系统模型可以充分反映系统高阶动态特性。但由于高阶系统对于噪声敏感，降低了模型预测精度，增加了预测模型的风险。因此，需要集成GM(1,1)模型的静态特性和ARIMA(4,1,1)模型的动态特性，给出库存量的最佳估计值。

4 基于信息熵的库存量集成预测模型

集成预测的基本出发点是：承认构造真实模型的困难，将单种模型预测看作代表或包括不同的信息判断，通过信息的集成，分散单项预测模型的特有的不确定性和减少总体的不确定性，从而提高预测模型精度。利用熵值法确定集成预测模型加权系数的基本思想是：某单一预测模型预测误差序列的变异程度越大，其在组合预测中对应的权系数就越小[15]。

在建立库存量预测灰色 GM(1,1)模型和ARIMA(4,1,1)模型后，采用信息熵方法实现子模型的集成，以准确预测库存量。

基于信息熵加权的计算步骤如下：

首先，计算第i个单一预测模型在t时刻的预测相对误差的比重pit。

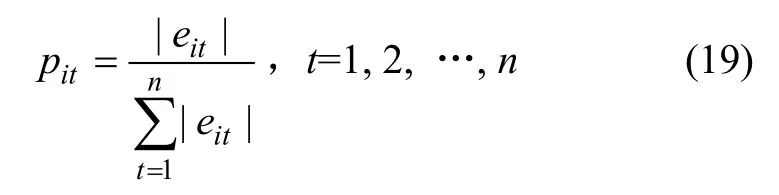
其中：eit为第i个预测模型在第t时刻的预测相对误差；n为预测样本个数为单一模型个数，本文中m=2。

其次，计算第i个单一预测模型预测相对误差的熵值Ei。

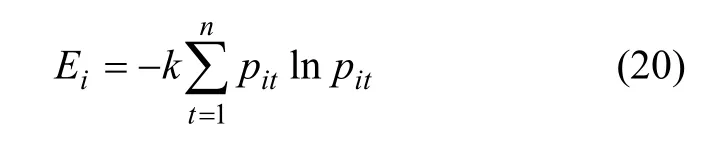
其中：k＞0为常数，ln为自然对数。对第i个预测模型而言，如果各个时刻所占比重相等，即2,…,n，那么，Ei取最大值，即Ei=klnn，本文取

然后，计算第i个单一预测模型预测相对误差序列的变异程度系数di。

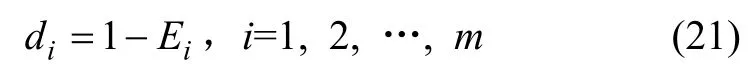
最后，计算各单一预测模型加权系数wi：

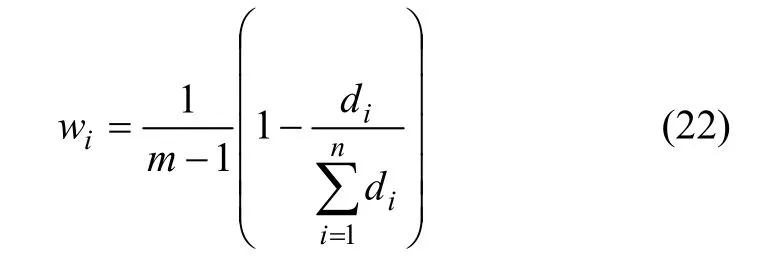
根据wi，集成预测模型的预测式为：

利用上述步骤，可以得到 GM(1,1)预测模型与ARIMA预测模型相对误差的熵值为：

由式(21)与E1和E2可求得2个单一预测模型预测相对误差序列的变异程度系数：

从而得到GM(1,1)模型与ARIMA模型的加权系数分别为：

则库存量集成预测模型为：

5 仿真验证及结果分析

以国内某钢铁企业某单种铁矿粉2010年4月至2010年7月的库存量历史数据进行分析及建模，数据样本个数为 100，分别根据上述步骤建立基于残差的等维信息GM(1,1)模型与ARIMA模型，并根据信息熵确定模型加权系数。

本文采用曲线及指标列表的方式对预测模型结果进行验证，评价指标分别采用：

(1) 最大误差Emax：

(2) 均方根误差(RMSE)：

均方根误差放大了误差，可以衡量不同模型之间的细微差别。

(3) 平均绝对相对误差(MAPE)：

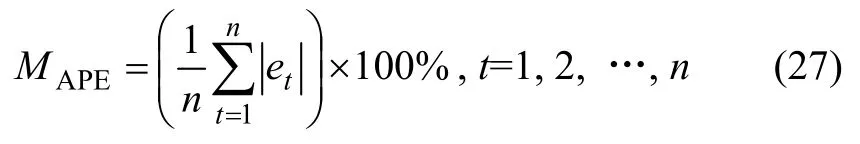
平均绝对相对误差能够反映预测的精度。

(4) 模型残差平均值：

式中：et为预测模型在第t时刻的预测相对误差；xt为第t时刻实际值；xˆt为预测模型在第t时刻的预测值。

根据上述4种评价指标，分别对GM(1,1)模型，ARIMA模型，集成预测模型进行结果分析，具体结果如表 5，预测模型预测曲线与误差曲线分别如图4与5所示。

根据仿真结果可知：本文所提出的基于信息熵融合的铁矿粉库存量质量预测模型依据子模型误差对各子模型输出进行合理加权，充分融合了GM(1,1)模型的静态特性和ARIMA(4,1,1)模型的动态特性，从而获得了较单一模型更高的预测精度，适用于钢铁企业铁矿粉原料的库存量的精确预测。

表5 库存量预测模型参数指标对比Table 5 Comparison of iron mine powders inventories prediction model indices

图4 3种预测模型预测曲线Fig.4 Predicting curves of three adopted models

图5 库存量预测误差曲线Fig.5 Inventories prediction error curves of three adopted models

6 结论

(1) 针对钢铁企业原料场库存量预测问题，提出一种基于灰色系统理论与时间序列的集成预测方法，构建了基于信息熵的集成预测模型。

(2) 对结果数据进行建模，降低建模的复杂度。

(3) 分别利用灰色预测模型适用于长期静态预测与ARIMA模型适用于短期动态预测的特点，结合二者优点进行集成预测。

(4) 利用信息熵方法以统计的形式确定集成模型的加权系数在理论上较为合理，并且模型仿真结果比较客观，证明该方法的有效性。

(5) 仿真所得到的预测精度已经满足企业对于库存量预测精度的要求，对于能够更加精确地预测库存量，以制定更为合理精确的采购计划，节约企业成本具有重大意义。

[1]刘国莉,唐立新,张明. 钢铁原料库存问题研究[J]. 东北大学学报: 自然科学版,2007,28(2): 172-175.LIU Guo-li,TANG Li-xin,ZHANG Ming. A study on raw material inventory in iron and steel industry[J]. Journal of Northeastern University: Natural Science,2007,28(2): 172-175.

[2]LI Shao-hua,TANG Li-xin. Improved tabu search algorithms for storage space allocation in integrated iron and steel plant[C]//2005 ICSC Congress on Computational Intelligence Methods and Applications. Piscataway: IEEE,2005: 1-6.

[3]Park C,Kim H,Kim J. Steel stock management on the stockyard operations in shipbuilding: A case of hyundai heavy industries[J].Production Planning and Control,2006,17(1): 1-12.

[4]Media A,Teddy A M. Analyzing and managing the disturbance in a mining port stockyard system[J]. Industrial Electronics &Applications,2010,3: 323-328.

[5]XU Jia,LIU Xiao-bin,WANG Ji-yan,et al. Raw materials collaborative inventory control model in iron & steel group[J].Computer Integrated Manufacturing Systems,2009,15(2):292-298.

[6]刘思峰,党耀国,方志耕. 灰色系统理论及其应用[M]. 3版[M]. 北京: 科学出版社,2004: 1-376 LIU Si-feng,DANG Yao-guo,FANG Zhi-geng. Grey system theory and application[M]. 3rd ed. Beijing: Science Press,2004:1-376.

[7]孙永荣,胡应东,陈武,等. 基于GM(1,1)改进模型的建筑物沉降预测[J]. 南京航空航天大学学报,2009,41(1): 107-120.SUN Yong-rong,HU Ying-dong,CHEN Wu,et al. Accurate estimation of building deformation based on improved grey GM(1,1) model[J]. Journal of Nanjing University of Aeronautics& Astronautics,2009,41(1): 107-120.

[8]崔杰,党耀国,刘思峰. 一种新的灰色预测模型及其建模机理[J]. 控制与决策,2009,24(11): 1702-1706.CUI Jie,DANG Yao-guo,LIU Si-feng. Novel grey forecasting model and its modeling mechanism[J]. Control and Decision,2009,24(11): 1702-1706.

[9]蒋大军. 运用 ARIMA预测烧结矿化学成分[J]. 烧结球团,2007,32(4): 24-30.JIANG Da-jun. Forecasting sinter component with ARIMA model[J]. Sintering and Pelletizing,2007,32(4): 24-30.

[10]LI Wei,ZHANG Zhen-gang. Based on time sequence of ARIMA model in the application of short-term electricity load forecasting[C]//Proceedings of 2009 International Conference on Research Challenges in Computer Science. Piscataway: IEEE,2009: 11-14.

[11]刘峰,王儒敬,李传席. ARIMA模型在农产品价格预测中的应用[J]. 计算机工程与应用,2009,45(25): 238-239.LIU Feng,WANG Ru-jing,LI Chuan-xi. Application of ARIMA model in forcasting agricultural product price[J]. Computer Engineering and Applications,2009,45(25): 238-239.

[12]易丹辉. 数据分析与EVIEWS应用[M]. 北京: 中国统计出版社,2002: 1-399.YI Dan-hui. Data analysis and EVIEWS application[M]. Beijing:China Statistics Press,2002: 1-399.

[13]WANG Xiao-guo,LIU Yue-jing. ARIMA time series application to employment forecasting[C]//Proceedings of 2009 4th International Conference on Computer Science and Education.Piscataway: IEEE,2009: 1124-1127.

[14]蒋金良,林广明. 基于ARIMA模型的自动站风速预测[J]. 控制理论与应用,2008,25(2): 374-376.JIANG Jin-liang,LIN Guang-ming. Automatic station wind speed forecasting based on ARIMA model[J]. Control Theory &Applications,2008,25(2): 374-376.

[15]韩超,宋苏,王成红. 基于ARIMA模型的短时交通实时自适应预测[J]. 系统仿真学报,2004,16(7): 1530-1535.HAN Chao,SONG Su,WANG Cheng-hong. A real-time short-term traffic flow adaptive forecasting method based on ARIMA model[J]. Journal of System Simulation,2004,16(7):1530-1535.