局部区域地形地貌生成方法
2011-07-07赵敏荣张曦文
赵敏荣, 张曦文
(空军工程大学理学院,陕西 西安 710051)
随着侦察手段的发展和侦察技术的提高,原有基于单一机动目标、实现更改颜色和简单的几何外形的伪装防护方法极易被精确制导武器所识别和定位。近年来,复杂背景中的目标检测与识别技术发展到了一个新的阶段,与之相适应,人们已经开始着手研究基于地貌环境特征的伪装方法研究,其实质是研究局部地形地貌的快速重建。
1 基于分形的目标识别与伪装方法
复杂背景下的图像检测与识别技术在军事目标识别、人脸与指纹识别、遥感图像处理等方面有着大量的应用。几十年来,国内外众多的学者和研究人员对复杂背景中的目标检测与识别进行了深入的研究,使复杂背景中的目标检测与识别技术发展到了一个新的阶段。但是,随着应用需求的提高,现有的技术和方法还有不足之处。因此,引入新的理论,发展新的技术和方法,成为这方面研究者重要的工作。分形为人们提供了一条新的途径,以自相似性为着眼点,强调了图像的自相似性,从而可以获得一个稳定的分维值或者分维变化值,而且克服了某些传统方法的缺点。国内外的学者都进行了一定的工作,取得了一定的成果,分形在目标识别众多方法中有着自己明显的优势。
1.1 分形维数[1]
由分形理论可以知道,越复杂的外形其表面就越粗糙,其分形维数也就越高;而被隐藏的目标则拥有比较简单的几何外形且表面光滑,其分形维数较低。分形理论中的分形维数恰好可以反映这种不同,因此准确地计算图像中目标的分形维数作为图像的分形特征数据就可以较好地对图像中的目标进行识别和判读。
因此,选用分形维数作为一个分形参数指标。将分形模型用于目标的伪装,使目标过高或过低的分维值隐藏在伪装模型之内,对外呈现出伪装模型的分维值。只要能够保证生成的伪装模型分维值与原始地形地貌环境的分维值相同,就可以被对基于分形技术的目标识别和判读认为两者的复杂程度、表面粗糙度和不规则程度是相同的,也就达到了实现地貌较好融合和良好伪装的目的。
1.2 分形模型吻合误差[2]
以分形模型拟合误差为基准进行目标检测的基本依据是:由于分形模型在一定尺度范围内可以很好的与自然背景相吻合,而人造物体却不能实现较好吻合。确定出一定的拟合误差数值上限,就可以保证生成的新模型与原模型的吻合程度较高,干扰敌方的情报分析人员利用基于分形模型的目标检测方法来发现军事目标,从而提高伪装效果,达到良好伪装的要求。现阶段研究数据表明,误差保证在 5%以内,就可以保证分形模型的吻合程度。
2 局部地形生成与实现的过程
分形技术已广泛的应用于地形模拟,但没与三维曲面重构相结合。由于分形地形模拟方法追求的是FBM的增量平稳性和自相似性,这样产生的地形其统计性是一致的。需要对生成伪装模型的形状进行控制干预,目前对其算法的生成结果控制有一定的研究,本文通过把利用一定的权值将缩放后的地貌模型曲面与分形曲面进行曲面融合,来控制生成图形的基本形状和轮廓,将分形几何模型与随机点生成技术及回归技术相结合,以生成与周围地貌环境相融合的局部区域模型来满足良好伪装的需要。
2.1 常用的分形算法[3]
地形建模是自然景物建模的一个很重要的分支。目前,许多分形地形建模方法都与分数维布朗运动(fBm)这一数学模型有关。随机中点位移程序用于正方形地平面生成地面特征,是一种较为常用的中点随机位移算法。其中的“菱形一正方形”细分法,是一种较为常用的中点随机位移算法。这种插值方法构成了一个双二次曲面的效果,它的一个重要优点是地形表面的法线是连续的,所以消除了三角形细分法中的折痕现象,而且该算法构造的地形轮廓比较柔和。并且可以通过调整系数值来决定表面粗糙度和山峰的陡缓,从而使三维地形地貌更加逼真,菱形—方形网算法生成随机分形地形的构网方式及实现:
第一经过菱形步时,以四个角的值为基准,如图1(a)中黑点所示。平均四个角的值,并加上符合一定分布规律的随机值。在图1(b)中,新值对应位置标志成黑点,原先已经存在的点显示为灰色。对于方形步,在相同的范围内生成随机值,这一步得到四个棱锥,它们在数组中心相交,计算四个菱形的中心,将小菱形的4个角平均之后作为新值的基数。图1(c)用黑点表示新值对应顶点,现有值为灰色。
接着进行第二遍迭代。先执行菱形步,这一步计算得到的4个四边形中心值标识为黑点,如图 1(d)所示;接着进行方形步,这时有 12个棱锥中心,如图1(e)中黑点所示,至此数组中全部25个元素都己经生成。如果分配更大的数组,则需要进行更多遍迭代,每一遍将加入更多细节。
这样对给定的正方形作一次细分迭代将得到4个四边形,第二次迭代将得到16个四边形,第三次迭代将得到 64个四边形。四边形数目等于22+i,其中i为递归经过细分过程的次数。
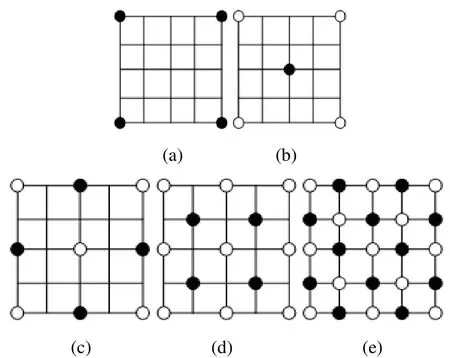
图1 菱形―方形网算法
设定随机分形菱形—方形网算法的四个初始点坐标为:(84,-143,1805)、(7800,7750,1880)、(457,-420,1805)、(8300,-7950,1880)。设定粗糙度为0.8,随机种子为20,权因子为0.8。从第一次迭代开始,就开始计算融合模型的分形维数,当其值与原始地形地貌的分形维数值的误差保持在 5%以内停止迭代。若多次迭代的误差仍不能控制在误差允许的范围之内,可适当调整随机种子数值。当迭代次数为6时,符合要求,停止迭代。其分形维数参数控制和分形地形显示如图2所示。

图2 随机分形曲面显示
随机分形地形的结果由其算法本身和迭代过程决定,与需要模拟的地形地貌和地貌模型无关。有可能会发生不一样的山体、地貌因其整体分形维数一致而生成一样的分形地形来,或者发生其维数虽与整体分形维数一致,但其分形图形明显与周围山体不相融合的情况。随机分形生成的地形虽然具有分形的特性,但在很大程度上是不能预测其生成结果的形状,作者既需要生成具有可控形状的模型,也需要其外形具有随机变化,以增强伪装效果。
2.2 局部区域源型选择[4]
把通过立体视觉技术测量得到的点云数据(3Dmodel1.txt),在Pro-E软件中读取,实现地形地貌的多角度显示,利用人机交互的方式在阵地地貌模型上直接选取。首先选取观察阵地地貌的最佳视觉角度,以便于全面、综合的观察地形地貌信息,其模型最佳视觉角度,选取出伪装区域模型的模拟原型,再对得到的模拟原型进行伪装需求分析和伪装支撑装置性能约束,综合考虑伪装区域利用率之后,确定适当的缩放系数,截取平面及原山包模型,截取后的山包模型显示如图3所示,作为伪装发育模型模拟的源型。

图3 局部区域模型模拟的源型
2.3 局部区域源型与随机分形模型融合[5]
伪装模型生成的主要目的是为了隐藏目标的需要,最重要的是要保证其基本外形与周围山体一致,保证其伪装模型在较大程度上显示预定目标模型的外形,另外加入的随机分形模型,也可以增强其外部形状的随机性,从而提高伪装模型的伪装效果。因此,需对预定目标模型和随机分形模型在最后伪装模型中占的比例进行设置。
在生成的随机分形地形中,设数据网格中点(x, y)的高程值为Z(x, y),即
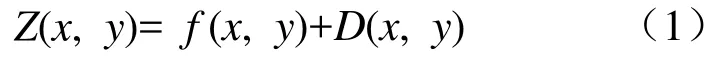
其中 D(x, y)是点(x, y)处的随机偏移量,在本文中选用的是一个均值为0,方差为σ2的高斯随机分布函数,而f (x, y)是点(x, y)周围四邻点的均值
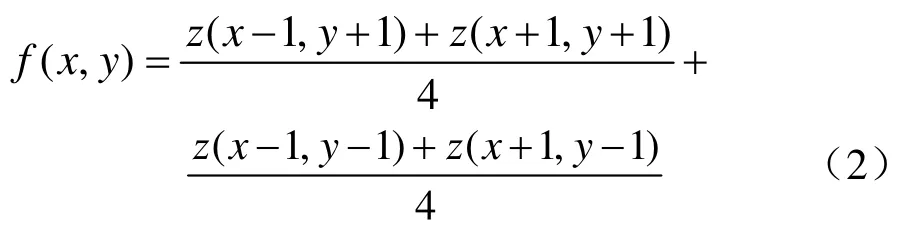
设控制源曲面上的点(x, y)处的高度值为Y (x,y),则Y (x, y)与随机量Z (x, y)之间存在一定的差值,设这个差值为offset,即
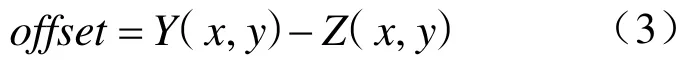
本文将利用这个差值来融合预定目标曲面与随机分形曲面,具体公式为
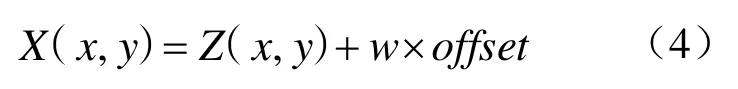
X (x, y)是最终点的高度值,w是设置的权因子。显然当w =0时, X( x, y )= Z( x , y);当w =1时, X ( x, y )= Y( x , y)。而当w在0和1之间变化时,如果w→0,则 X( x, y)会更趋近于Z( x, y),也就是说融合后生成的曲面更接近于随机分形曲面;如果w→1,则X( x, y)会更趋近于Y( x, y),也就是说融合后生成的曲面更接近于控制源曲面。
3 实 例
局部地形地貌的快速生成,最重要的是要保证其基本外形与周围地貌一致,保证其作为伪装模型时在较大程度上显示预定目标模型的外形,另外加入的随机分形模型,也可以增强其外部形状的随机性,从而提高伪装模型的伪装效果。
利用Pro-E软件对目标控制区域地貌模型和随机分形地貌模型的点云数据进行读取。为了区分方便,将目标控制区域地貌模型的三维点云数据进行网格划分,如图3中网格部分所示;对随机分形地形点云数据进行直接显示,如图3中小黑点部分所示。把利用菱形―方形网算法生成随机分形地形,得到随机分形曲面图1,与图2所示的局部区域源曲面,结合设计的权因子,利用Pro-E软件进行曲面融合得到符合要求的局部区域图3,对生成的局部区域模型进行拟合后显示如图4所示。在外形上能够实现与周围地貌环境的较好融合。
图4 局部区域地形地貌显示
4 结束语
本文针对分形在目标检测和识别技术中的应用,研究了分形几何在分形地形模拟地貌而生成的方法,并提出了局部区域生成算法,它以比较小的代价,实现了快速表达三维地理信息,以生成与地形相似的目标隐形外形。
[1]英振华. 基于分形理论的地形场景实时真实感绘制[D]. 重庆: 重庆大学, 2005.
[2]Pentland A P. Fractal description of natural exenes [J].IEEE, 1984, 6: 661-674.
[3]忠 宝, 房亚冬, 赵 锋, 等. 用 FBM 方法生成山脉地形的真实感图形方法[J]. 计算机工程与应用,2004, 32: 33-35.
[4]康晓清, 曲仕茹. 基于融合曲面造型方法的预定形状山脉地形生成[J]. 西北工业大学学报, 2004, 22(5):626-629.
[5]Falconer K. Fractal geometry-mathematical foundations and applications [M]. New York: John Wiley &Sons,1990: 119-139.
