基于AR双谱的超声波电机故障诊断

陈智博，黄宜坚

(华侨大学 机电及自动化学院，福建 厦门，361021)

超声波电机(Ultrasonic motor，USM)是伺服系统中一种新型的直接驱动微特电机，它利用在超声波频率范围内的机械振动作为驱动源的驱动器[1]。与传统电磁电机相比，超声波电机不依靠电磁相互作用来传递能量，具有无电磁干扰、动作响应快等优点，在精密控制领域要比传统电磁电机性能优越[2]。因此，如何判断超声波电机工作正常以及准确发现故障问题，具有重要的意义。当前，常用的故障征兆提取方法多是假设振动信号具有平稳和高斯分布的特性，并基于这种数学特性进行故障诊断，如功率谱估计和时频分析方法[3-4]。而在实际工程中，信号或噪声不一定服从高斯分布，或待分析的系统不是线性最小相位系统等，此时，基于自相关函数的功率谱估计难以满足实际的要求。高阶谱分析方法是近年来信号处理领域中涌现出来的一种新的数学工具，与传统的信号处理方法不同，它可进行非高斯信号处理[5-6]。双谱是三阶累积量的二次Fourier变换，它保留了信号的相位信息，可以定量地描述信号中与故障密切联系的非线性相位耦合，还可以抑制噪声的影响，消除高斯噪声的干扰[7-9]。目前，利用高阶谱累积量的参数化模型研究超声波电机系统机械故障的资料很少。本文作者根据超声波电机工作时的非进给方向微小振动的变化特点，用三阶累积量对其平稳振动信号建立AR模型(Autoregressive model)，计算 AR双谱，提取双谱的特征，进而得出一种有效的超声波电机故障诊断方法。

1 超声波电机测试装置

1.1 测试对象

超声波直线电机由超声波电机和高精度直线电机组成，如图1所示。该装置安装于三轴转台上，超声波电机具有1自由度并作直线运动，下端高精度直线电机同样作1自由度直线运动，方向互为90°。

图1 超声波直线电机Fig.1 Ultrasonic motor and linear motor

超声波电机产生故障的主要原因，一是定子与转子摩擦时，由于微凸体的存在, 产生跳跃、滞后等现象，造成接触非线性；二是当外部电压出现瞬间的阶跃式掉电现象。当发生以上故障时，振动信号包含系统的各种噪声干扰和信息直接由传感器检测出来。因此，在实际工作中，分析有色噪声信号就可以判断出超声波电机是否出现了故障。

1.2 实验测试装置

测试系统的硬件有工控机、以色列 Nanomotion公司的直线超声波电机，Advatech公司的2路12位D/A卡、三轴正交编码计数器以及 Renishaw公司的RGH24H30D30A型光栅尺(分辨率50 nm等)。采集程序为Borland C编写。整个系统的总体方案如图2所示。该系统的控制器通过PC机软件实现。USM产生的振动信号用下端的互相垂直的光栅尺进行检测。

图2 测量系统原理图Fig.2 Block diagram of measuring system

2 累积量的时序模型与参数化AR双谱分析模型

2.1 累积量的时序模型

用滞后量m和n表示变量x(t)的3阶累积量函数c(m，n)为：

对于稳定的物理过程，可用 x(t)的 3阶累积量表示，可以写为：

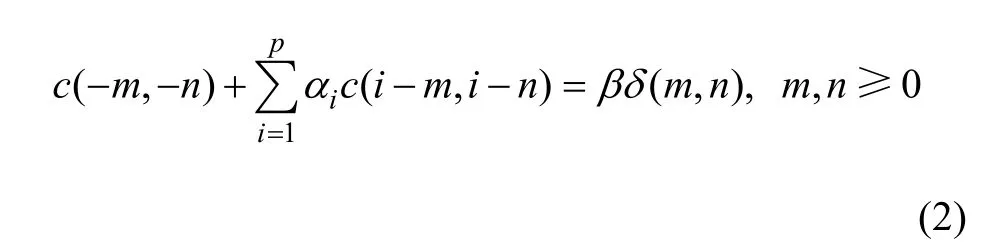
式中：δ(m，n)为二维单位冲激函数。

在式(2)中令m=n，可得{x(k)}的3阶自相关c(m，n)的对角切片值，令m，n=1，2，…，p，可得：

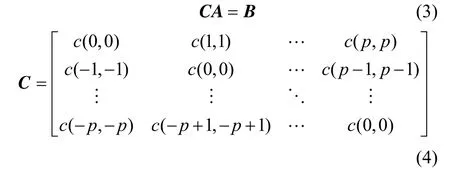
2.2 AR模型与双谱

超声波电机的输出振动所含的随机信号是其在振动过程中受到均值为0的非高斯白噪声a(t)的干扰，x(t)为零均值的有色非高斯噪声。所以，输出的随机信号中含有系统的丰富动态信息，可以建立AR模型：

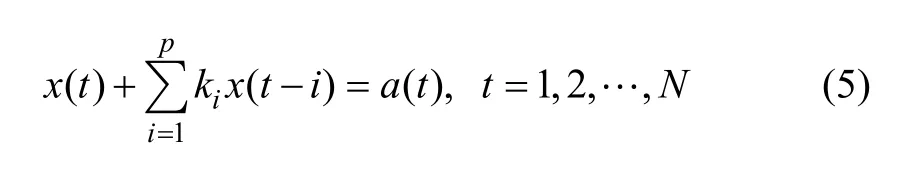
式中：ki(i=1，2，…，p)为自回归系数；p为自回归模型的阶数。

根据定义，随机量 x(t)的双谱为 3阶矩的二维Fourier变换，即

从而，双谱可以写成：

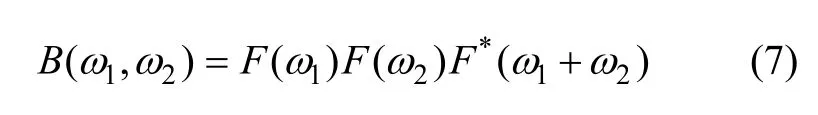
式中：F(ω)是 x(t)的 Fourier 变换；F*(ω)是 F(ω)的共轭复数；双谱B(ω1，ω2)是复函数。

参数法表示振动信号的双谱 B(ω1，ω2)可以表示为：

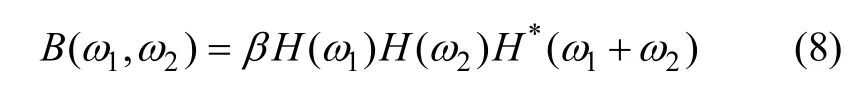
式中：H(ω)为 X(n)在 3阶统计意义下的 AR模型；H*(ω1，ω2)为 H(ω1，ω2)的共轭复数。

2.3 AR模型阶次

参数化双谱估计面临确定模型阶次的问题，基于信息论的一些准则(如AIC等)，在估计AR模型阶次时，以二阶统计为基础，而且应用了高斯过程的似然函数，所以，这些准则对于有色高斯测量噪声的感染不能胜任。而累积量含有相位信息，具有抗有色噪声的能力，所以，利用高阶累积量的方法确定模型阶次可信更高。定义振动信号的双谱互相关系数：

式中：D(ω1，ω2)表示序列的直接法双谱估计；B(ω1，ω2)表示序列的参数化双谱估计；rc(p)描述了2种估计结果的相关程度。因此，模型的最佳阶次为：

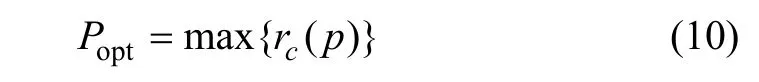
可见，阶次p预测过程中包含的样本相关。过高或过低的阶次会导致频谱出现“假峰”或“失真”现象。SVD Frobenius法确定的阶数p效果较好[10]，一般p取 8～10。

3 实验数据处理与分析

3.1 参数化双谱分析

基于AR模型的双谱估计方法用于估计非高斯包噪声通过p阶AR模型产生的输出序列的双谱。将长度为N的观测数据{x(i)}分成K段长度为M的数据，并且段与段之间有一半的数据重叠，则2N=KM。

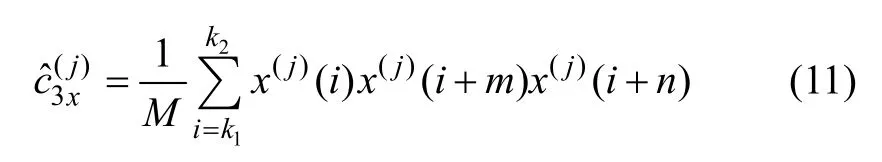
3.2 数据预处理

光栅尺所记录到的超声波电机微弱振动信号，由于现场各种噪声干扰存在，可能会使测量数据发生某种缓慢的位移趋势，导致频谱的误差加大并使频谱的低频段发生变形，因此，必须对此进行滤波，消除趋势项，减少或消除采样数据的干扰成分。中数法是一种很好的滤波算法，通过3次均值的方法消除趋势项，使数值处于零均值附近，从而得到比较真实的振动噪声，如图3所示。

图3 原始数据与滤波后结果Fig.3 Raw data and reconstructed results

在实验过程中，为超声波电机设置了2类的不同的故障：一类为 USM 机械与材料的物理损伤，导致运动不稳定、不均匀、不连续、滞后甚至于堵转；另一类为电气(电源)，现象为电压或电流的幅值变化、频率波动、波形畸变，甚至于断电。本实验采用了典型的故障数据样本，具体设置如表1所示。

表1 超声波典型故障类型Table 1 Fault classification for ultrasonic motor

故障Ⅰ和故障Ⅱ为机械故障，故障Ⅲ为电气故障。故障Ⅰ中 USM 的定、转子表面出现较为明显的摩擦刮痕，运动轨迹流畅但存在间断性抖动，位移幅值过大时有尖锐的噪声；故障Ⅱ为定、转子的严重磨损状况，其运动有很明显的滞后性与运动不稳定，表面温度快速升温，转子和定子出现轻微开裂；故障Ⅲ为USM的机械部分无异常，但USM控制器因电源芯片部分管脚焊锡脱落，电压输出引脚与接地引脚均出现接触不良，导致输出电压与控制电压存在波形畸变现象，电压电流有异常幅值抖动，由于 USM 控制器的实时控制补偿，运行轨迹出现微弱的抖动。

3.3 AR双谱图分析

双谱是三维空间的函数。图4～7所示分别为超声波电机在正常和故障状态下的双谱图和其等高线图。从图4可以看到：在正常情况下，谱峰数量少，位置比较集中，谱峰幅值层次非常清楚，峰值在ω1为处急剧收敛，并出现尖锐峰值；而在故障Ⅰ情况下，双谱图峰值减少，在主要几个峰值附近呈现出区域扩大现象，非主要频谱区的峰值也变得较为平缓；在故障Ⅱ时，双谱图则没有关键点的峰值，峰谱很小且数量较多，峰值没有明显层次区别，谱峰位置比较分散；在故障Ⅲ时，双谱图与正常状况下的双谱图相似，不过局部峰值则有不同程度减少，峰值在处减少为原来的40%，其余频谱区也变得较为平滑。2种情况下的谱峰位置不同，这是由于频率成分以及各频率分量之间发生平方相位耦合的情况不同而反映出来的必然结果[13]。

图4 正常状况的振动信号的双谱分析Fig.4 Analysis of bispectrum in normal state

图5 故障Ⅰ的振动信号的双谱分析Fig.5 Analysis of bispectrum in fault Ⅰ

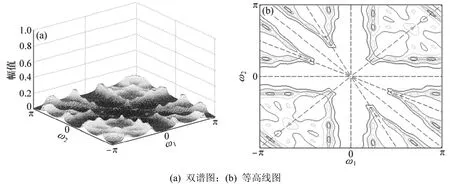
图6 故障Ⅱ的振动信号的双谱分析Fig.6 Analysis of bispectrum in fault Ⅱ

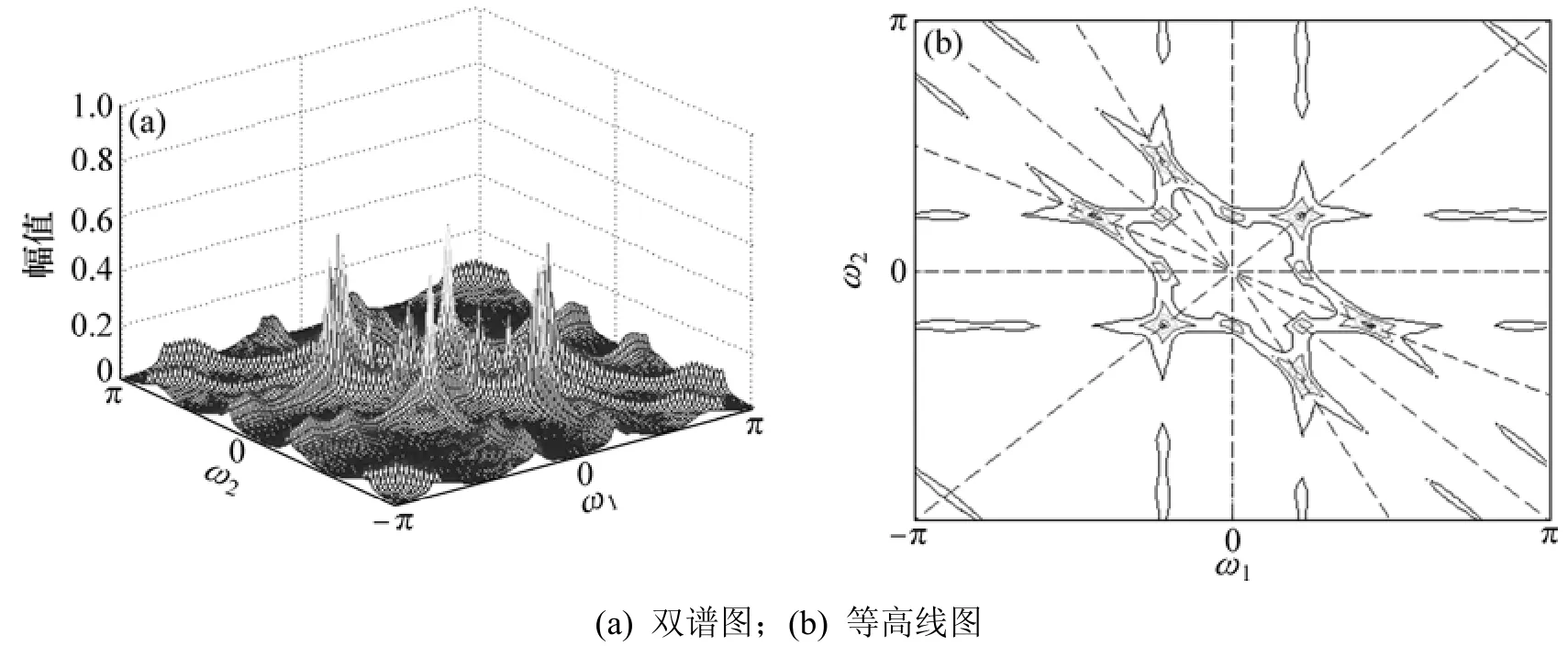
图7 故障Ⅲ的振动信号的双谱分析Fig.7 Analysis of bispectrum in fault Ⅲ

从等高线的分布情况来看，在正常情况下，等高线图所覆盖的频率面积较小，且双谱能量急剧收敛在几个关键的频率点上。在故障状况时，等高线覆盖面积开始逐步扩大，最终达到大面积覆盖(图6)，分布较为分散。等高线图的覆盖频率面积也开始增大，双谱能量也开始流向各个频段(图7)。

双谱的对角线切片就是11谱。图 8所示为超声2波电机正常和故障状态下的AR双谱对角线切片图。在正常状况下，能量集中在频带较窄，幅值较大。而在故障状况下，图8(b)和图8(d)中能量集中在幅值较小，图 8(c)中集中在，谱峰的分布频率不明显。除在故障频率会产生明显的谱峰下降外, 就只有一些零散的小波峰。

3.5 重构的功率谱

图9所示为双谱重构的功率谱。ω2=0或ω2=π处的切片是关于ω1=0对称的，因为周期为2π。在处的切片是不对称的。 重构的功率谱与AR双谱说明它们反映出的主频变化规律是一致的, 只是某些细节信息不同, 而这些细节信息正是由于信息本身含有的非高斯、非线性原因所导致[14]。从超声波电机的振动信号的功率谱图很难区分电机的不同工作状态，这是由于定子和转子的个别部件工作状态变化导致了信息的非高斯、非线性，但是AR双谱以及其谱切片就能清晰地分辨出超声波电机的不同工作状态。

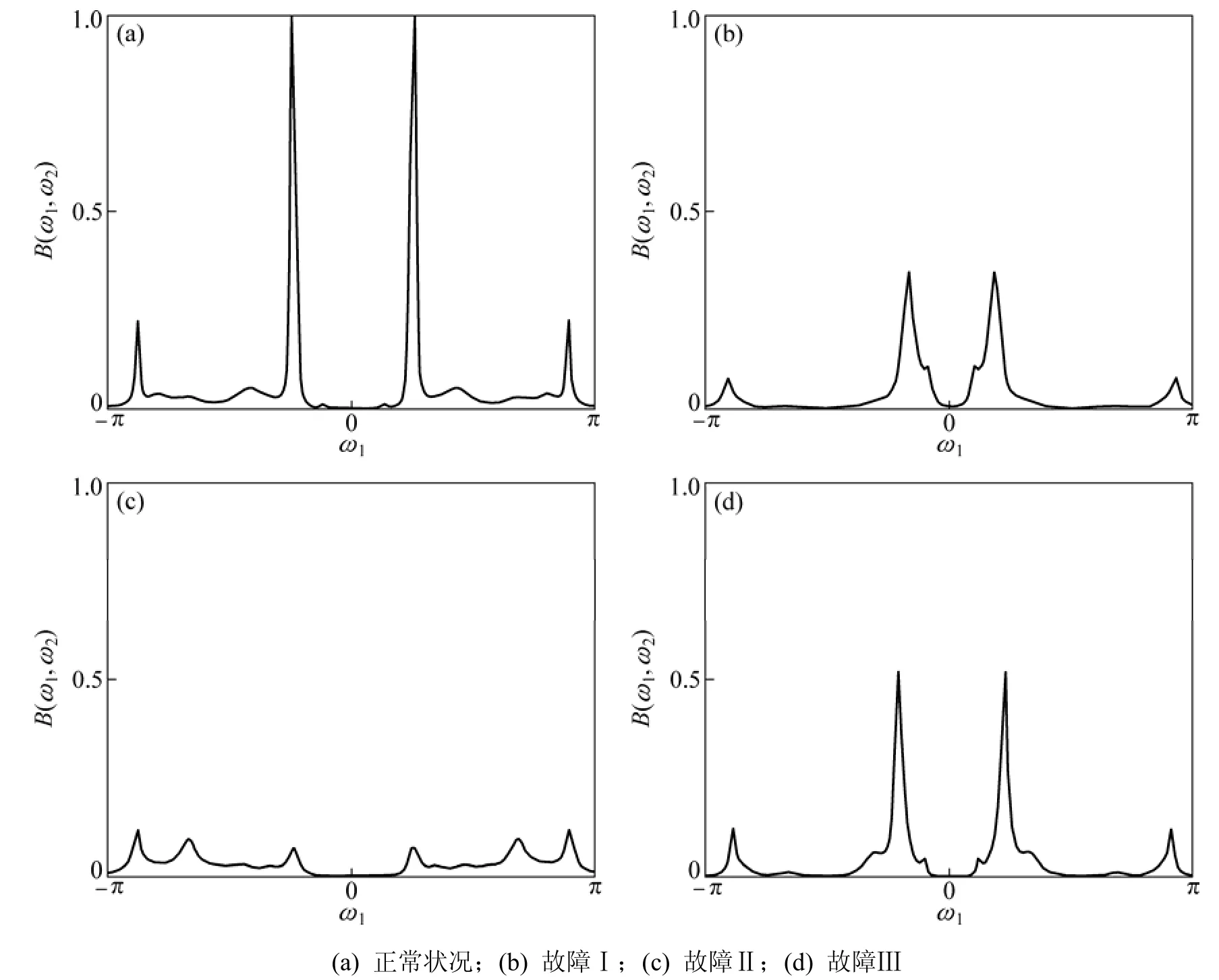
图8 不同状态下AR双谱维切片图Fig.8 dimensional slices of bispectra in different states

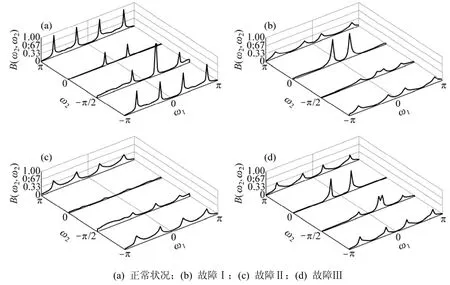
图9 双谱重构的功率谱Fig.9 Contours from reconstructed AR power

4 结论

(1) AR双谱函数属于参数建模，它不受采样数据的样本限制，即使在样本数据较少的情况下，也具有较高分辨率的双谱估计。

(3) 利用 AR 双谱重构功率谱，可以抑制高斯有色噪声的干扰，得到传统功率谱无法获得的功率与频率关系的信息，包含了更多的非线性细节。

(4) 根据正常和故障状况的双谱结构图、等高线图和切片图的差异，可得出一种诊断超声波电机故障的方法。

[1] Tashiku S, Takashi K. An introduction to ultrasonic motors[M].Oxford: Clarendon Press, 1993: 355-359.

[2] 金龙, 褚国伟, 胡敏强, 等. 超声波电机速度与定位控制系统[J]. 中国电机工程学报, 2005, 25(1): 131-136.JIN Long, CHU Guo-wei, HU Min-qiang, et al. The speed and position control system of Ultrasonic motor[J]. Proceedings of the CSEE, 2005, 25(1): 131-136.

[3] 陈皓. 电力系统故障暂态信号的功率谱估计[J]. 电力自动化设备, 2002, 22(6): 12-15.CHEN Hao. Power spectral estimation of power system fault transient signal[J]. Electric Power Automation Equipment, 2002,22(6): 12-15.

[4] 徐世艳. 经验模态分解的时频分析方法及其应用[J]. 吉林大学学报, 2009, 27(5): 487-492.XU Shi-yan. Time-frequency analysis method and its application based on empirical mode decomposition[J]. Journal of Jilin University, 2009, 27(5): 487-492.

[5] 张贤达. 时间序列分析[M] . 北京: 清华大学出版社, 1999:11-13.ZHANG Xian-da. Time series analysis[M]. Beijing: Tsinghua University Press, 1999: 11-13.

[6] 张贤达. 现代信号处理[M]. 北京: 清华大学出版社, 1995:263-281.ZHANG Xian-da. Morden signal processing[M]. Beijing:Tsinghua University Press, 1995: 263-281.

[7] Nikias C L, Mendel J M. Signal processing with higher order spectra[J]. IEEE Signal Processing Magazine, 1993, 10(3):10-37.

[8] Walsh D, Delaney P A. Detection of transient signals in multipathenvironments[J]. IEEE Journal of Oceanic Engineering,1995, 20(2): 133-138.

[9] Rauge J A, Pike C M, Sullivan E J. Active sonar detection in multipath: A new bispectra analysis approach[J]. Circuits Systems Signal Process, 1994, 13(4): 455-466.

[10] 蒋雨燕, 黄宜坚. 调速阀故障诊断的 AR双谱定阶方法比较[J]. 华侨大学学报, 2009, 30(2): 123-126.JIANG Yu-yan, HUANG Yi-jian. Comparison of different methods of determining the order of autoregressive Bi-spectrum[J]. Journal of Huaqiao University, 2009, 30(2):123-126.

[11] 沈申生, 华亮. 超声波电机摩擦和磨损特性探究[J]. 润滑与密封, 2006, 10(10): 192-195.SHEN Shen-sheng, HUA Liang. Research on friction and wear properties of ultrasonic motor[J]. Lubrication Engineering, 2006,10(10): 192-195.

[12] 华亮, 吴晓, 张建生. 超声波电机堵转特性及堵转检测方法研究[J]. 电气传动, 2008, 38(10): 73-77.HUA Liang, WU Xiao, ZHANG Jian-sheng. Research on the characteristics and detection methods of locked-rotor state for traveling-wave ultrasonic motor[J]. Electric Drive, 2008, 38(10):73-77.

[13] Colis W B, White P R, Hammond J K. Higher-order spectra: The bispectrum and trispectrum[J]. Mechanical System and Signal Processing, 1998, 12(3): 375-395.

[14] 黄宜坚, 杨建红. 电流变仪的AR三谱切片特性[J]. 湘潭大学自然科学学报, 2008, 30(3): 73-79.HUANG Yi-jian, YANG Jian-hong. AR trispectra slice characteristics of electro-rheometer[J]. Natural Science Journal of Xiangtan University, 2008, 30(3): 73-79.