液黏传动变形界面间油膜温度场实验研究

谢方伟，侯友夫，张立强，袁晓明，宋喜福，席涛

(1. 江苏大学 机械工程学院，江苏 镇江，212013；2. 中国矿业大学 机电工程学院，江苏 徐州，221008)

液体黏性传动(简称液黏传动)是20世纪70年代中期发展起来的一种新型流体传动形式[1]，是继液压、液力传动之后，第3种以液体为工作介质的传动技术，它基于牛顿内摩擦定律，利用油膜剪切力来传递动力，具有高效节能、无级调速、启动冲击小和同步传动等特点，在带式输送机、风机、水泵等大功率重载设备的调速启动方面具有广阔的应用前景[2-3]。液黏传动装置工作过程中，摩擦副间存在滑差导致热量产生，油膜的温度升高，油膜的动压承载力和传递的扭矩减小，这将严重影响液黏传动装置的工作性能。Jang等[4]综合考虑热效应和表面粗糙度对液黏传动装置的影响，对流体润滑状态下液黏传动装置接合过程中的瞬态热效应进行分析，建立了相应的雷诺方程。洪跃等[5]采用幂律型非牛顿流体模型，考虑表面粗糙度和表面沟槽等对液黏传动装置中的摩擦副间油膜状态进行了数值计算与分析。陈宁[6]考虑油膜与摩擦副之间的对流换热，对混合摩擦阶段液体液黏传动装置的热负荷进行了理论分析计算。Jen等[7]对摩擦副接合过程中产生的热量进行理论和实验研究，采用分离变量法建立数学模型，对摩擦副接合过程中的温升及温度场分布进行数值模拟，并与实验结果对比分析。Meng等[8]建立了修正瞬态雷诺方程、热能量方程和工作油黏温方程，通过数值计算对液黏传动装置工作过程中油膜的温度场、压力场、传递扭矩和油膜承载力进行了研究，并得出工作油的温升对油膜承载力和油膜传递扭矩的影响规律。Xie等[9]构建了液黏传动对偶片瞬态温度场理论模型，并采用有限元法进行求解，得到了对偶片温度场的分布特点，指出温差引起的热应力导致了对偶片产生一定程度的变形，部分揭示了摩擦副的变形机理。到目前为止，在研究液黏传动机理时，均假设摩擦副为绝对平行的刚性平面。由于摩擦副通常较薄，研究发现混合摩擦阶段摩擦副热应力耦合导致其发生翘曲变形，从而引起摩擦副间油膜流动状态发生变化，影响油膜温度场的分布特性。本文作者采用计算流体动力学软件 FLUENT对油膜温度场进行数值模拟和实验研究，以揭示液黏传动摩擦副间油膜的温度分布特性及变形界面对油膜温度场的影响，为液黏传动技术的研究和液黏传动装置的设计提供理论依据。

1 基本方程

根据流体力学可知，流体的流动所遵守的基本守恒定律主要包括质量守恒定律、动量守恒定律和能量守恒定律。该守恒定律可以用质量守恒方程、动量守恒方程和能量守恒方程进行数学描述[10-11]。

(1) 质量守恒方程：

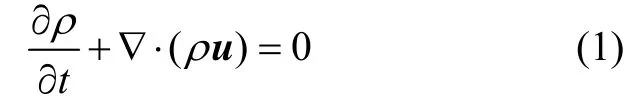
对于定常流动的不可压缩的流体，ρ为常数，式(1)可写为：

式中：ux，uy和uz分别为油膜在x，y和z方向上的速度分量。

(2) 动量守恒方程。动量守恒方程即Navier-Stokes方程的一般形式如下：

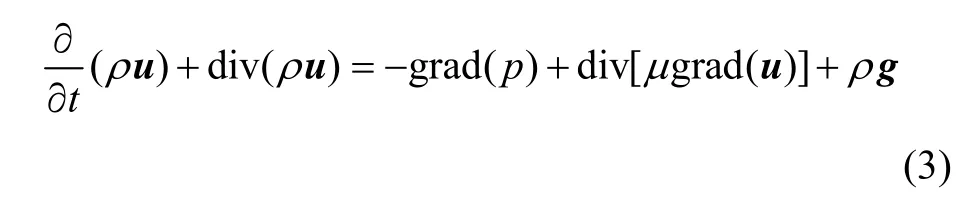
式中：μ为油膜的动力黏度；p为油膜的压力；g为重力加速度。

(3) 能量守恒方程

式中：cp为比热容，J/(kg·℃)；t为温度，℃；k为流体传热系数；ST为流体的内热源及由黏性作用流体机械能转换为热能的部分。

2 计算模型

研究发现混合摩擦阶段热应力耦合导致摩擦副发生翘曲变形，利用所研制的实验台，研究对偶片的热应力和变形情况，利用 CNC全自动三坐标测量仪进行平面度的测量(如图 1所示)，测量的对偶片的轴向变形量如图2所示。由图2可知：对偶片最大变形量为0.103 mm；变形量与半径近似呈线性关系。

图1 变形对偶片的测量Fig.1 Measurement of deformed steel disk

摩擦副是液黏传动装置传递动力的主要部件，由摩擦片和对偶片组成，如图3所示。该摩擦副的摩擦片表面共有20个沟槽，其间油膜物理模型如图4所示。油膜的几何参数如下：油膜内径为 130 mm，外径为180 mm，油膜的厚度为 0.5 mm，沟槽的深度为 0.5 mm。根据油膜的对称性，取1/20油膜(即1个沟槽区和1个无沟槽区油膜，且两者对称布置)进行分析，油膜两侧面做周期性边界条件设置，这样可保证只研究20个沟槽中的1个即可反映整体油膜的状态。

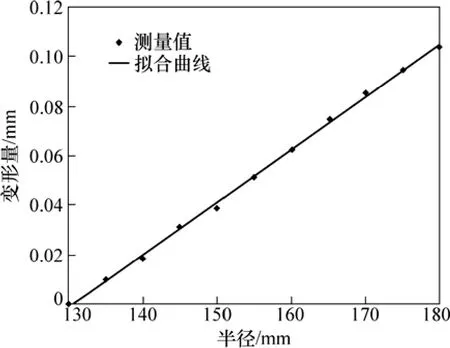
图2 对偶片轴向变形量Fig.2 Axial deformation of steel disk

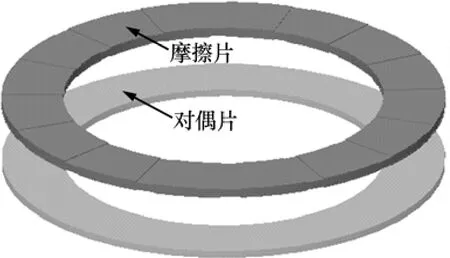
图3 摩擦副三维模型Fig.3 3-D model of friction pair

图4 摩擦副间油膜物理模型Fig.4 Oil film model between friction pair

利用计算流体动力学原理，采用有限体积法并选用大型商用软件FLUENT进行求解[12]。图5所示为油膜物理模型及边界条件设置，图中剪头所示为运动壁面的旋转方向。油膜边界条件设置如下：运动壁面旋转速度ω为1 000 r/min，壁面无滑移，入口总压为0.3 MPa，出口总压为0 MPa，油膜的两侧面为周期性边界条件，考虑油膜的黏温特性，采用UDF编写热源函数和黏温特性函数，然后初始化所有变量，进行迭代求解。

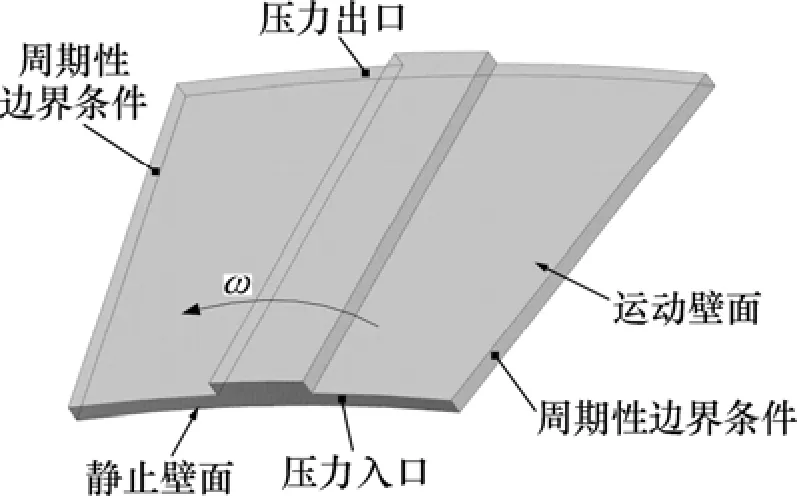
图5 1/20油膜物理模型及边界条件Fig.5 1/20 physical model and boundary conditions of oil film

3 计算结果

为了更直观显示径向压力和周向压力的变化情况，在油膜上取3条线：沟槽底面的中心线1；无沟槽区的中心线2；在圆周方向半径160 mm，油膜厚度0.4 mm处取1条圆弧3，对应的圆周角θ的变化范围是0°～18°。这3条线在油膜上的相对位置如图6所示。

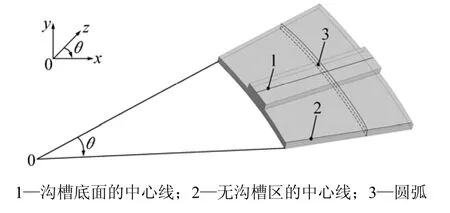
图6 3条线在油膜上的相对位置Fig.6 Relative position of three lines on oil film

图7所示为平行界面和变形界面间油膜温度沿径向的分布。由图7可知：2种工况下油膜的温度沿径向均随半径位置的增大而升高。由于沟槽区冷却油的流量大，冷却充分，沟槽区油膜的温度远低于无沟槽区；变形界面间油膜温度略低于平行界面间油膜的温度，原因是油膜的流动速度增加，相同时间带走的热量增多。

图8所示为平行界面和变形界面间油膜温度沿周向的分布，为便于观察温度沿周向的分布规律，图中给出3个沟槽的温度沿周向的分布，对应的圆周角范围是 0°～54°，沟槽区的范围分别为 6°～12°，24°～30°和 42°～48°，无沟槽区的范围分别为 0°～6°，12°～24°，30°～42°和 48°～54°。由图 8 可以看出：沟槽区油膜温度明显低于无沟槽区的油膜温度，沟槽区油膜温度沿摩擦片旋转的反方向逐渐降低；无沟槽区油膜温度从无沟槽区域的一侧到另一侧温度先逐渐升高，接近另一侧时温度达到最高；变形界面间油膜的平均温度略低于平行界面间油膜的温度。

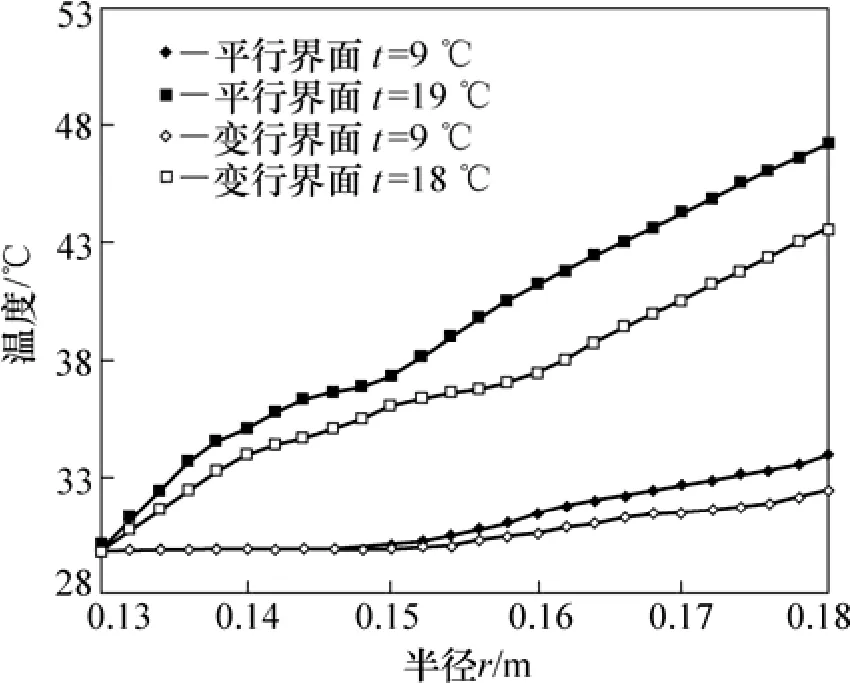
图7 油膜温度沿径向的分布Fig.7 Temperature distribution of oil film along radial direction

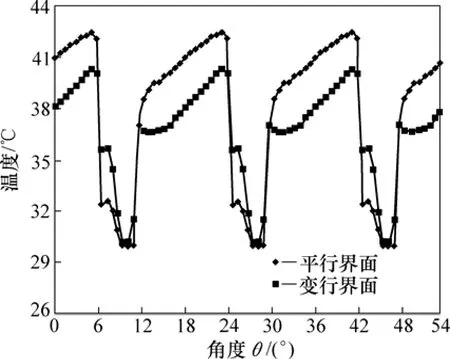
图8 油膜温度沿周向的分布Fig.8 Temperature distribution of oil film along circumferential direction

4 实验研究

为了验证数值计算的正确性，搭建了液黏传动实验台，并进行大量的实验研究。液黏传动实验台如图9所示。图10和图11分别为平行界面和变形界面间油膜温度随时间的变化，其中，t1～t4分别对应有沟槽区半径为135，145，165和175 mm处的测点温度；t5～t8分别为无沟槽区半径为135，145，165和175 mm处的测点温度。由图10和图11可知：平行界面和变形界面间油膜的温度随时间的变化规律基本相同，即在所测量的时间范围内油膜的温度随时间的延长而升高；油膜的温度与时间近似呈线性关系升高，无沟槽区的温度明显高于有沟槽区的温度；变形界面有沟槽区和无沟槽区油膜的温度均略低于平行界面间油膜的温度。

图9 液黏传动实验台Fig.9 Hydro-viscous drive test bed

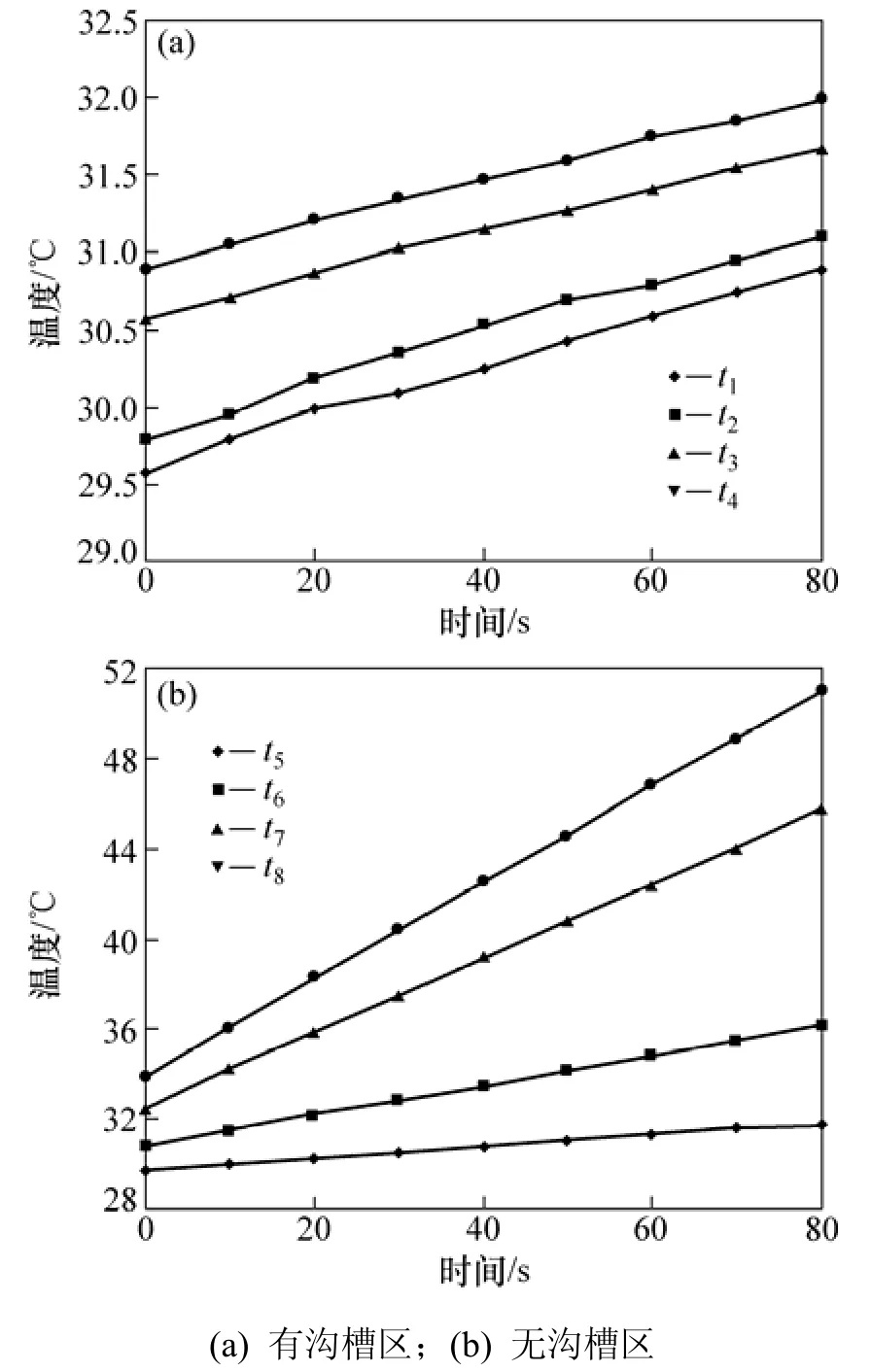
图10 平行界面间油膜温度随时间的变化Fig.10 Variation of oil film temperature with time between parallel interfaces under 5 L/min

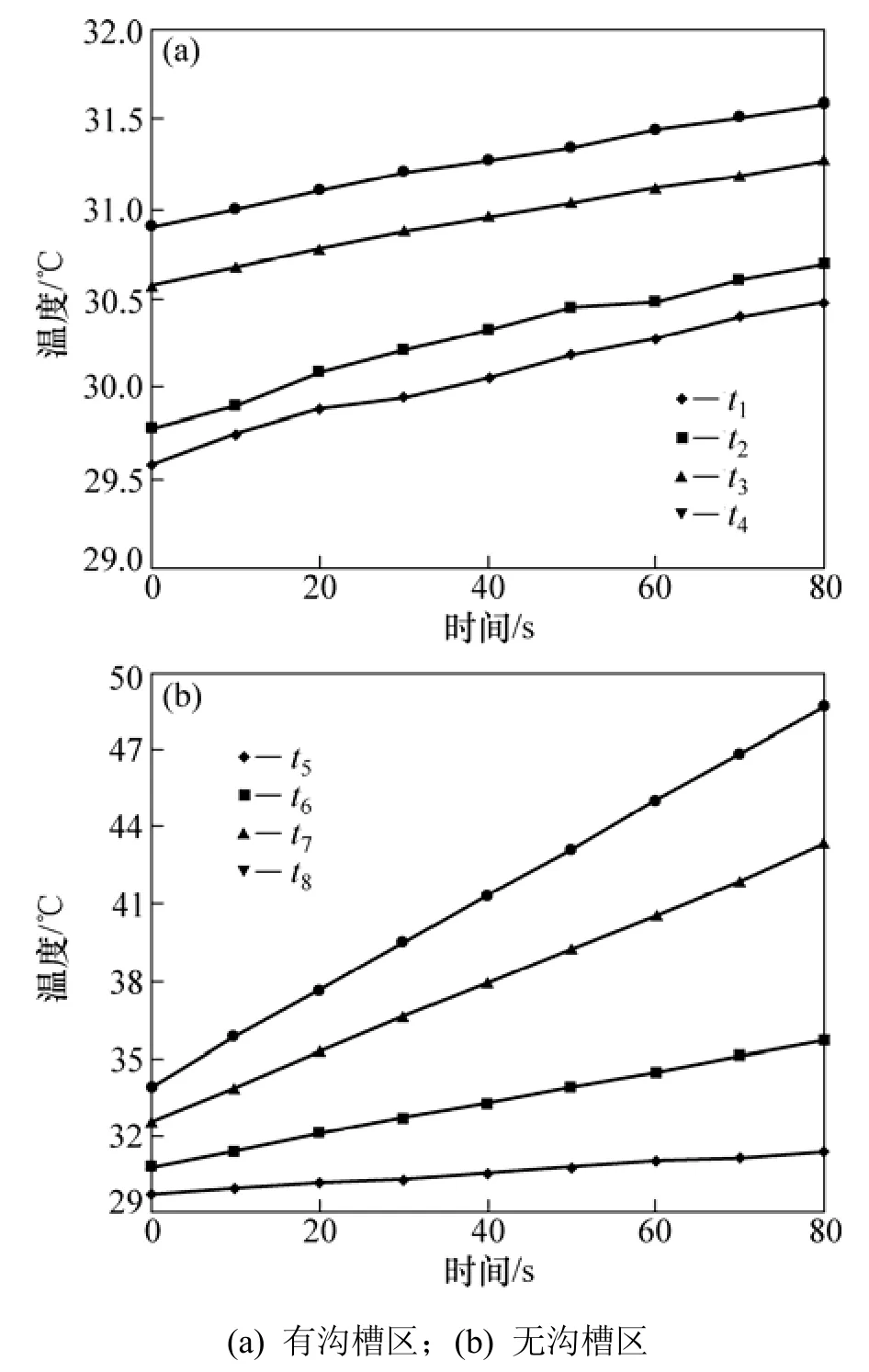
图11 变形界面间油膜温度随时间的变化Fig.11 Variation of oil film temperature with time between deformed interfaces under 5 L/min

当实验进行30 s时，对平行界面和变形界面间油膜的温度进行测量。图12所示为油膜温度沿径向的变化。由图12可知：平行界面和变形界面间油膜的温度沿径向递增，且与半径近似呈线性关系；有沟槽区油膜的温升较小，约为1 ℃，而无沟槽区温升约为10 ℃；变形界面间有沟槽区和无沟槽区油膜温度均略低于平行界面间油膜的温度。

图13所示为在温度测量区测点沿周向的布置图。沟槽区和无沟槽区测温点的位置为：以沟槽的1边为基准，圆周角分别为 3°，6°，12°和 18°，半径为 165 mm的圆周上各布置1个温度传感器，测点温度分别用t9，t10，t11和t12表示。图14所示为油膜温度沿周向的变化。由图 14可知：沟槽区油膜的温度(t9)最低，无沟槽区油膜的温度(t11)最高，且沟槽两边的温度略有不同(t10略低于t12)，沟槽区温度明显低于无沟槽区；平行界面间油膜的温度略高于变形界面间油膜的温度。

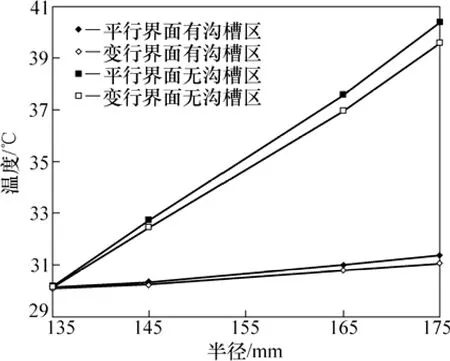
图12 油膜温度沿径向的变化Fig.12 Variation of oil film temperature along radial direction

图13 温度测点沿周向的布置图Fig.13 Arrangement diagram of temperature measuring points along circumferential direction

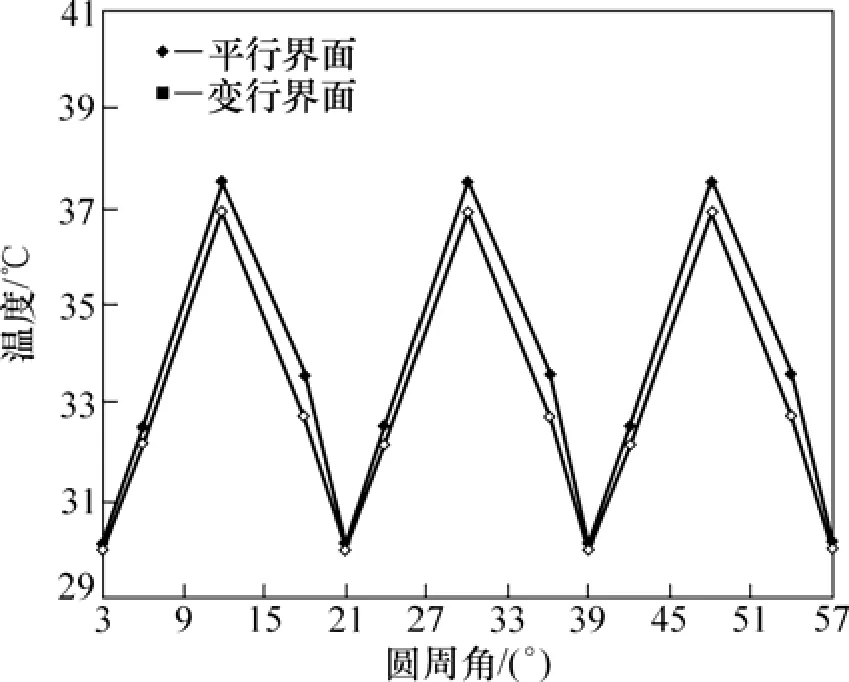
图14 油膜温度沿周向的变化Fig.14 Variation of oil film temperature along circumferential direction

5 结论

(1) 在实验测量的时间范围内，平行界面和变形界面间油膜的温度随时间的延长而升高；油膜的温度与时间近似呈线性关系升高，无沟槽区的温度明显高于有沟槽区的温度。

(2) 在同一时刻，平行界面和变形界面间油膜的温度沿径向递增，且与半径近似呈线性关系；有沟槽区油膜的温升较小，约为1 ℃，而无沟槽区温升约为10 ℃；变形界面有沟槽区和无沟槽区油膜的温度均略低于平行界面间油膜的温度。

(3) 沟槽区油膜温度沿摩擦片旋转的反方向逐渐降低；无沟槽区油膜温度，从无沟槽区域的一侧到另一侧温度先逐渐升高，接近另一侧时温度达到最高；变形界面间径向温度略低于平行界面间油膜的温度，原因是油膜的黏度降低，流动速度增加，相同时间带走的热量增多。

[1] 魏宸官, 赵家象. 液体黏性传动技术[M]. 北京: 国防工业出版社, 1996: 1-3.WEI Chen-guan, ZHAO Jia-xiang. Hydro-viscous drive technology[M]. Beijing: Defense Industry Press, 1996: 1-3.

[2] 张以都, 张启先. 液体黏性软启动装置的启动特性研究[J].北京航空航天大学学报, 2002, 28(5): 578-580.ZHANG Yi-du, ZHANG Qi-xian. Investigation on start behavior of hydro-viscous transmission[J]. Journal of Beijing University of Aeronautics and Astronautics, 2002, 28(5): 578-580.

[3] HOU You-fu, MENG Qing-rui. Dynamic characteristics of conveyor belts[J]. Journal of China University of Mining &Technology, 2008, 18(4): 629-633.

[4] Jang J Y, Khonsari M M. Thermal characteristics of a wet clutch[J]. ASME Journal of Tribology, 1999, 121: 610-617.

[5] 洪跃, 刘谨, 金士良. 液体调速离合器中摩擦副热效应的简化分析[J]. 润滑与密封, 2003(5): 6-11.HONG Yue, LIU Jin, JIN Shi-liang. Simplified thermal effect analysis of frictional disk in speeding wet clutch[J]. Lubrication Engineering, 2003(5): 6-11.

[6] 陈宁. 液体黏性传动技术的研究[D]. 杭州: 浙江大学机械工程学院, 2003: 88-98.CHENG Ning. Theoretical and application researches on hydro viscous drive[D]. Hangzhou: Zhejiang University. Department of Mechanical Engineering, 2003: 88-98.

[7] Jen T C, Nemecek D J. Thermal analysis of a wet-disk clutch subjected to a constant energy engagement[J]. International Journal of Heat and Mass Transfer, 2008, 51(7/8): 1757-1769.

[8] MENG Qing-rui, HOU You-fu. Effects of friction disc surface groove on speed-regulating start[J]. Industrial Lubrication &Tribology, 2009, 61(6): 325-331.

[9] XIE Fang-wei, HOU You-fu. Transient temperature field of a friction pair in a HVD device of a belt conveyor[J]. Mining Science and Technology, 2010, 20(6): 904-907.

[10] Rogers S E, Kwak D. Upwind Differencing scheme for the time-accurate incompressible Navier-Stokes equations[J].American Institute of Aeronautics and Astronautics Journal,1990, 28: 253-262.

[11] Merkle C L, Althavale M. Times accurate unsteady incompressible algorithms based on artificial compressibility[J].American Institute of Aeronautics and Astronautics Journal,1987, 87: 125-132.

[12] 李建平, 王伯长, 刘涛, 等. 侧喷加热铝材退火炉内流场与温度场数值模拟[J]. 中南大学学报: 自然科学版, 2010, 41(1):166-171.LI Jian-ping, WANG Bo-chang, LIU Tao, et al. Numerical simulation of flow and temperature field in side-down aluminum annealing furnace[J]. Journal of Central South University:Science and Technology, 2010, 41(1): 166-171.