改进参数化方法及在低空风切变中的应用

胡朝江，杨全法，李晓冲，袁有志

（北京航空技术研究中心，北京 100076）

最优控制问题的计算方法很多，归纳起来，可以分为直接法和间接法两大类[1]。直接法中的参数化就是通过把控制变量、状态变量和时间参数化的方法来进行求解，这种方法具有简单、直观的特点。但参数化方法也存在很多不足之处，其中最重要的一点就是，利用参数化方法转化得到的非线性规划问题由于维数过高，求解难度较大，因此严重影响了这种算法的推广应用。为此，有必要对该算法进行改进，从而使该算法更适合于求解最优控制问题。

1 算法简介

1.1 参数化算法求解最优控制问题的思路

一般的最优控制问题可描述为：确定随时间而变化的容许控制向量，使得由一组非线性微分方程所描述的动力学系统由初始状态0过渡到终端状态f，并同时使某一性能指标J达到最小，如能量消耗最小，过渡时间最短等[1]。

参数化方法求解最优控制问题的基本思路是将控制状态的时间历程参数化，从而得到一个高维非线性规划子问题，通过对转化而得的高维非线性规划问题的求解，从而获得对应的最优控制问题的解。

由于对高维非线性规划问题求解难度很大，因此影响了该算法的推广使用。为此，经过分析认为，对一类最优控制问题在对其参数进行离散化时，可以仅对其控制变量的时间历程参数化，而不需对其状态变量的时间历程也参数化，就极大地降低了转化而得的非线性规划子问题的维数，从而使求解变得容易。

1.2 改进的参数化算法简介

改进算法仅对控制变量参数进行离散化处理，而对状态变量的值，在已知状态初值和控制规律的情况下，则可通过积分动力学微分方程进行求解。因此，最优控制问题就转换成了以节点处的控制变量取值为变量的非线性规划子问题，而动力学微分方程也转换为以节点处的控制变量值为自变量的非线性约束条件。考虑到将要求解的最优控制问题的终端时间不给定，为此，由最优控制理论可知，对应的泛函指标可采用下面的形式

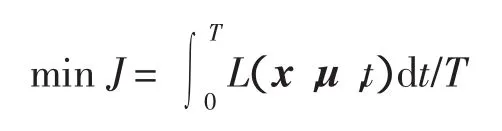
式中：J为目标函数；x为状态向量；u为控制向量；T为终端时间；L为x，u和时间t的标量函数。为此，对应的改进算法如下：

1.2.1 将终时不给定的最优控制问题化为终时给定的最优控制问题，方法是：

1）设终端时间T为可变参数，引入新的时间变量τ∈[0，1]，定义 t=Tτ；

2）引入增广状态变量及状态方程：xn+1=TL（x，u，t），xn+1（0）=0，将目标泛函化为：min J=J[x（1）]，x（1）=[x1（1），…，xn（1），xn+1（1）]T。

1.2.2 将对应的最优控制问题化为非线性规划子问题，方法是：

1）将时间区间τ∈[0，1]m等分，得到m+1个节点；

2）引入一组向量 pi作为节点 τi，i=0，1，…，m-1处控制变量的估计值，节点之间控制变量值由相邻两点线性插值确定。

1.2.3 建立的非线性规划子问题目标函数为

即此时的目标函数变成了以节点处的控制变量值pi和终端时间T为自变量的函数，其中控制和状态变量满足相应的约束条件。

1.2.4 求解相应的非线性规划子问题

由于所转化而成的非线性规划子问题与同时离散状态变量和控制变量时所转化而成的非线性规划子问题相比，所得的非线性规划子问题的维数大幅降低，因而极大地降低了求解问题的维数，因此，用一般的非线性规划问题求解方法就可以顺利求解。对要求解的非线性规划子问题，采用了序列二次规划算法进行求解，求解的基本步骤如下[2]：

1）初始化：给定最优控制问题的微分方程阶数n，节点数m，控制变量阶数q，状态初值x0，状态终值xf，控制变量在节点处的初始估计值，积分时间参数T估计值，控制变量及时间T的上、下限约束等；

2）梯度及函数计算：

计算函数 x（1）及约束 x（1）-xf，这里=[p0，p1，…，pm-1，T]

3）求解二次规划子问题的搜索方向△yk；

4）修正当前解 yk+1=yk+ △yk；

5）若当前解满足误差要求，则最佳解求出，停止计算。否则，若当前迭代次数小于最大迭代次数，则继续迭代，否则，停止计算，计算失败。

2 算例

低空风切变对飞机的飞行安全威胁很大[3]，为此利用改进算法求解了飞机在低空风切变中的最优着陆轨迹控制问题。为了简化问题的求解，假设飞机在铅垂平面内运动，风场也作用在飞机运动的铅垂平面内，则在风切变中的飞机质心运动方程可描述如下

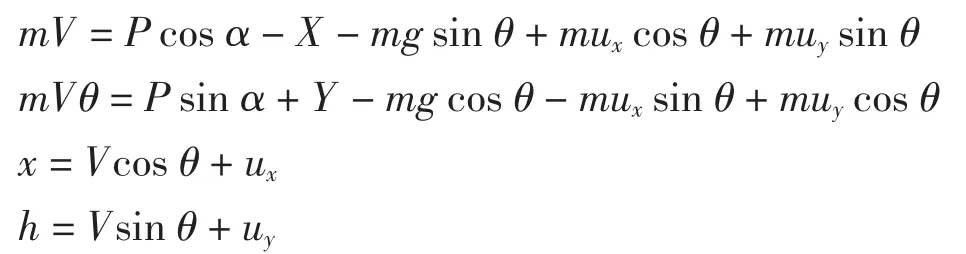
方程中：m为飞机质量；g为重力加速度；V为飞行速度；P为发动机推力，为油门位移和飞行速度及高度的函数；Y、X分别为飞机升力、阻力，均为迎角、飞行速度、飞行高度及机翼面积的函数；θ为飞机下滑的轨迹角；α为飞机迎角；x、h为分别为飞机在水平和垂直方向的位移；ux，uy分别为风速在水平和垂直方向的分量。

风切变模型具有下面的形式[4]

式中：ux0和uy0分别表示水平和垂直风幅值；T0为穿越下冲暴流的总飞行时间。

飞机在风切变中着陆的最优控制问题可描述为通过对迎角α和油门δp的适当控制，使飞机能够穿越风切变区并安全着陆。飞机状态变量初值和终值分别为

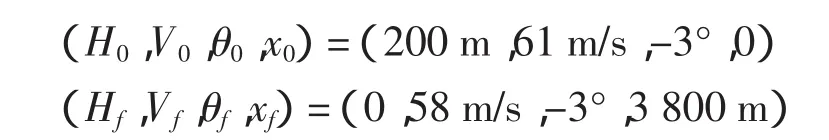
控制变量满足的上下限约束条件

式中罚系数k的取法如下

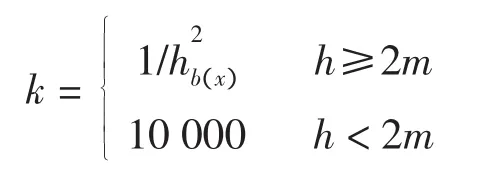
风场强度取为（ux0，uy0）=（16 m/s，8 m/s）。

利用改进的参数化算法求解所得的结果如图1～图3所示。

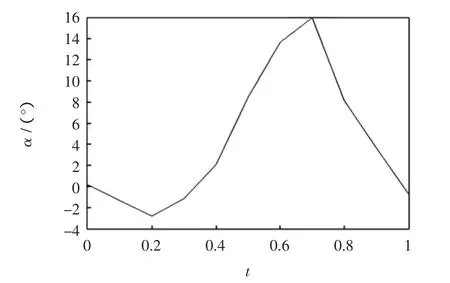
图1 迎角控制律Fig.1 Control law about AOA

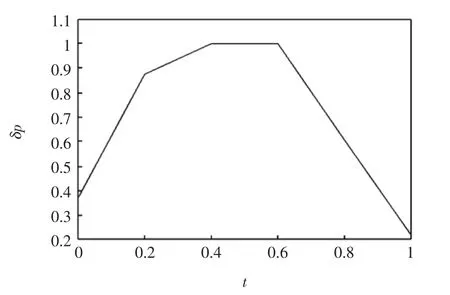
图2 油门控制律Fig.2 Control law about throttle

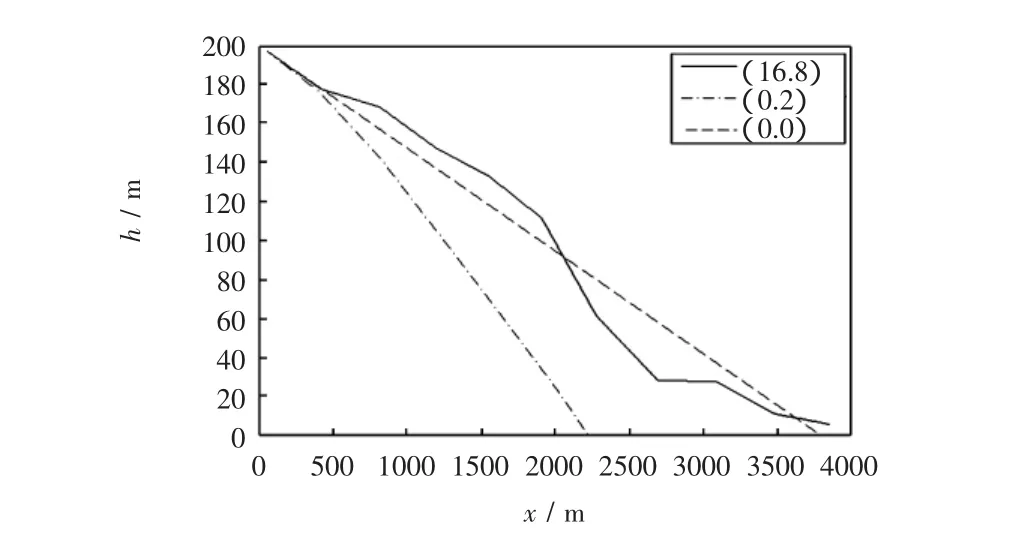
图3 风切变中的飞行轨迹Fig.3 Flight path in wind shear

其中图1为求得的迎角控制规律，图2为求得的油门控制规律，图3为相应的飞机在风切变中着陆的轨迹。图3中虚线为正常无风情况下的着陆轨迹，点化线为风场强度为（ux0，uy0）=（0，2 m/s）时，仍按无风情况下进行控制的着陆轨迹，实线为风场强度为（16 m/s，8 m/s）时按改进算法求出的飞机在风切变中的着陆轨迹。由图3的点划线可知，当飞机遭遇风切变时，如不采取相应的控制方法，则即使遭遇较弱的风切变流场，飞机也很难安全着陆，主要表现为飞机提前接地。而由图3的实线可知，如采取正确的控制方法，即使飞机遭遇较强的风切变，也可以保证安全着陆。同时该算例也说明，本文提出的最优控制算法，可以顺利求解一类最优控制问题。

3 结语

最优控制问题是航空航天以及国民经济建设的许多领域都会面临的问题，如何求解最优控制问题是人们普遍关心的话题。已有的求解方法中，每种方法各有其利弊，本文针对直接求解方法的不足进行了必要的改进，改进后的算法一是大幅降低了转换而得的非线性规划子问题的维数，降低了问题的求解难度；二是缩短了求解最优控制问题的时间，有利于实现实时最优控制，三是有利于求解多控制变量问题。因此，通过改进，非常有利于参数化算法在求解最优控制问题上的推广应用。

[1]吕显端.最优控制理论基础[M].北京：科学出版社，2008.

[2]张立卫.最优化方法[M].北京：科学出版社，2010.

[3]胡朝江.大风机风切变告警系统[J].中国民航大学学报，2008，26（5）：23－25.

[4]MIELE A，WANG T.Optimal Landing Trajectories in the Presence of Windshear[J].Journal of optimization and applications，1988，58（2）：165－202.