基于经验模态分解的图像拼接

张晓宇， 戴 芳， 甘明辉， 王赛芳



基于经验模态分解的图像拼接

张晓宇， 戴 芳， 甘明辉， 王赛芳

（西安理工大学理学院，陕西西安710054）

对待拼接图像分别进行经验模态分解，对分解得到的第一个固有模态函数与第二个固有模态函数的叠加进行特征点提取、特征点匹配与变换矩阵的估计以实现图像的拼接，文中提出的方法有效提高了特征点匹配的正确率，具有很强的鲁棒性。在图像融合方面文中提出一种新的基于余弦关系变换的加权融合技术，在实现图像无缝拼接的同时，可有效去除拼接图像重叠区域的重影与鬼影现象。

计算机应用；图像拼接；经验模态分解；余弦关系变换

图像拼接是将一组相互间存在重叠区域的图像序列实施配准，进而融合成一幅完整、无缝、宽视野、高分辨率新图像的技术。图像拼接技术现已广泛应用于显微图像分析、空间探测、医学图像分析处理、虚拟现实技术、遥感数据处理、军事侦察、公安取证和数码相机超分辨处理等方面，具有广泛的应用前景。

图像拼接的关键技术是图像配准与图像融合。在图像配准中基于图像特征点的配准方法是该领域的研究热点，该方法是对待配准的两幅图像提取满足特定要求的特征点，然后对这两组特征点进行匹配，生成一组特征点匹配对，利用这组匹配点对间的对应关系估计出全局变换参数，以实现图像配准。该方法的优点是运算速度较快，配准精度由特征点的提取精度以及特征点匹配精度决定，因此选择和提取具有鲁棒性的特征点以及提高特征点匹配的精度是本文研究的重点。

传统Harris角点检测算法只能在单一尺度下进行特征点检测，特征点的提取过于依赖阈值的选取，易受噪声点的影响而产生偏移现象。为解决这一问题，近年来有学者利用小波变换对图像进行分解，在多尺度下进行角点提取，并取得一些成果，但小波变换的分解方法本质上是一种适合于线性信号分析的方法，它将信号按照固定的小波基进行分解，在分解过程中丢弃了信号的某些局部特征，而且在小波基的选取上也具有一定的主观性。针对以上问题，结合经验模态分解(Empirical Mode Decomposition, EMD)对非线性、非平稳信号分析的优越性，本文利用经验模态分解技术对待拼接图像进行分解，在分解后得到的固有模态函数(Intrinsic Mode function, IMF)的基础上进行Harris角点检测及特征点匹配，以提高特征点提取及匹配的正确率，实现高质量图像拼接。

本文的具体安排如下：第二部分介绍经验模态分解的基本原理，并给出对图像进行经验模态分解的算法步骤；Harris角点检测的基本原理在第三部分给出；第四部分介绍归一化相关法在本文特征点匹配中的改进与应用；第五部分介绍了RANSAC(Random Sample Consensus)算法及最小中值法的基本思想并给出了变换矩阵估计的算法步骤；第六部分是图像拼接和融合，介绍一种基于余弦关系变换的加权融合技术，并将融合效果与传统的0-1渐变加权融合进行了比较；第七部分为实验结果与性能分析；最后为结论。

1　经验模态分解

经验模态分解是1998年由Huang等人提出的一种自适应变尺度多分辨分析方法，它利用信号自身特征进行信号分解，可以把非平稳、非线性信号按照频率由高到低的顺序逐层筛选，分解成一组稳态、线性的数据系列集，即固有模态函数集。

经验模态分解的基本原理是找出信号的局部极大值和局部极小值点，对这些点进行插值，获得信号的上、下包络和均值包络，然后利用筛选算法把符合固有模态函数的信号依次分解出来，即把一个信号分解成若干个固有模态函数和残差信号之和。

固有模态函数是原始信号本身所包含的最基本的信号组成单元。它必须同时满足下列条件：① 数据极值点和过零点数目必须相等或至多相差1；②在任意点由局部极大值点构成的包络和局部极小值点构成的包络的平均值为0。

利用经验模态分解对图像进行分解的具体步骤如下：

（1）求出图像的局部极大值点和局部极小值点；

（2）对图像极大值点和极小值点分别进行三次插值，生成上、下包络曲面；

（3）对上、下包络曲面取平均得到平均曲面；

（4）从图像中减去平均曲面：-=；

（5）将作为新的重复步骤(1)～(4)，直到r满足IMF的条件，此时得到第一个固有模态函数，记为；

（6）从原始图像中减去，对得到残差图像再重复上面的筛选过程得到第二个固有模态函数；

（7）对与取和，记为=+。

是对图像分解后得到的第一个固有模态函数，包含原图像大量的高频信息，反映原图像细节及轮廓方面的信息；是图像分解得到的第二个固有模态函数，表示图像的次高频信息。对与进行叠加得到的具有固有模态函数固有的局部波形对称等优点，在保留了大量原始图像信息的同时，还能剔除噪点、光线不一致等意外因素造成的影响，因此在上进行操作能有效提高特征点的提取精度与特征点匹配的准确率。

2　特征点提取

基于图像特征的配准方法首先是要尽可能准确地提取出图像的特征点。在众多方法中Harris角点检测由于其在一致性和有效性方面的优良性能一直被人们所推崇。该方法提取的特征点具有旋转、平移不变性，且可以达到亚像素级的精度；对噪声和光照条件的影响也具有一定的鲁棒性。所以本文采用Harris角点检测器对经EMD分解后的第一个固有模态函数与第二个固有模态函数的叠加进行角点检测，以获得理想的检测结果。

Harris角点检测是通过微分运算和自相关矩阵运算来检测信号点特征的位置，即通过下列响应函数来体现

其中

（2）

阈值的设置具有主观性，设置的过大会造成特征点错选和漏选，而设置过小又将导致计算量的增加。为此本文首先根据值进行局部非极大值抑制以确保得到的点均为局部极值点，再对检测到的局部极值点按照值大小进行降序排列，提取前个点作为特征点，进入下一步特征点匹配。这样就避免了阈值设置的主观性带来的上述影响，同时又得到一批数目稳定、适中的最优特征点。

3　特征点匹配

对两幅待拼接的图像进行经验模态分解，分别获得和，其中是第一幅图的前两个固有模态函数的叠加，为第二幅图的前两个固有模态函数的叠加。然后分别对和进行特征点提取，对获取的特征点进行匹配，以寻找对应的同名点。本文采用归一化相关法(Normalised Cross-Correlation, NCC)进行特征点匹配，它的基本思想是依据待拼接图像上对应角点邻域像素灰度值的相似性进行匹配，设T和S分别为以待拼接图像与上的角点为中心，大小为´两个相关窗口，、为两图相关窗口内像素灰度值的均值，则定义角点之间的相关系数为

本文在进行角点匹配时，对中的每一角点p与中的所有角点进行匹配，即计算p与中所有角点的相关系数值，寻找中与p相关系数最大的角点作为p点的匹配点，其中，对图像中的个角点遍历完毕后即可产生个特征点对，对产生的特征点对按照值的大小降序排序，对匹配过程中产生的“多对一”误匹配情况采取全部剔除的操作，然后在所得特征点对中按照黄金分割0.618的比例，根据相关系数值由大到小截取一定数量的最优匹配点对，从而确保得到足够数量及精度的匹配点对，避免了匹配过程对阈值选取的过度依赖。

4　变换矩阵估计

由于相机的运动、透镜作用和光源变化等一些复杂因素，相机获取的图像序列必然存在光强差异、反光区域以及坐标系不一致等问题，因此为了实现图像序列的拼接，首先必须确定这些图像序列间的空间对应关系。目前常用的图像间的变换关系模型有平移变换模型、刚性变换模型、仿射变换模型以及投影变换模型。本文采用的是仿射变换模型，利用齐次坐标以矩阵的形式来描述该模型为

即为变换矩阵，通过式(4)将待变换图像经平移、旋转、缩放变换到参考图像坐标系下。

经过特征点匹配以后，在两幅像间产生一个对应特征点集。要实现图像间的拼接，理论上直接从匹配点对中随机抽取三对匹配点即可将计算出来，但经过归一化方法在剔除了部分偏差过大的点对后，得到的特征点对仍然存在误差，直接使用这些点对估计变换矩阵误差会很大，因此要得到最优的变换矩阵还要经过一个筛选和优化的过程。本文采用RANSAC(Random Sample Consensus)算法与最小中值法(least Median squares)相结合来估计最优变换矩阵。

RANSAC是一种鲁棒性的拟合数据算法，它能充分利用测得的数据，根据阈值把它们分成内点和外点。由于内点数据比较准确，因此RANSAC使用内点来进行参数估计。

最小中值法的基本思想是计算所有匹配点数据的余差，取其中值作为标准，把满足小于中值的匹配点作为优化样本来重新估计最优的变换矩阵。变换矩阵估计算法如下：

（1）随机选取3对匹配点，利用式(4)计算变换矩阵；

（2）对待拼接图像上的每一个特征点利用计算它在图像中的对应点，并计算该对应点与在中的匹配点之间的距离差d，称为余差；

（3）根据RANSAC算法中内点距离小于阈值的原则，设定阈值，并将d<对应的特征点对作为此次估计的内点集合，记录内点数目，在此内点集合内重复步骤(1)重新估计；

（4）重复步骤(2)、(3)，经过次随机采样后得到最大内点集合以及与之对应的变换矩阵；

（5）运用最小中值优化算法对进行优化估计。首先对步骤(4)中得到的内点进行次随机采样，每个子样本为3个匹配点对，根据式(4)计算出每个子样本的变换矩阵M{M|=1, 2,…,}；然后，在最大内点集合内对每个矩阵M分别计算出与之对应的个特征点对间余差的平方r_,{r_,|=1, 2, …,;=1, 2, …,}，取每组余差平方的中间值U=(r_,)；寻找U中的最小值以及与其对应的变换矩阵；用在最大内点集合内再次计算个特征点对间余差的平方_min,{r_, |=1, 2, …,}，取_min,所对应的匹配点对作为最优的样本空间，对最优样本点进行优化处理求得最优变换矩阵。

5　图像拼接与融合

变换矩阵确定后，接下来的工作就是将图像进行配准。设为参考图像，为待配准图像，本文采用后向映射法对进行配准，即给出新坐标系（参考图像所在的坐标系）下每个点的坐标，利用变换矩阵寻找其在上的对应点，并将处的像素值提取作为新坐标系下该点处的像素值，但因为通过计算得到的和值并非整数，要得到处的像素值，还需运用双线性插值进行处理。

配准完成后，开始对图像进行拼接融合。图像融合是将配准后的图像序列进行拼接，增加图像信息量并消除接缝的过程。常用的拼接图像平滑过渡方法是加权平均融合法（即渐入渐出法）。假如、是两幅已配准待拼接图像，将图像和进行拼接融合，则融合后的图像可表示为

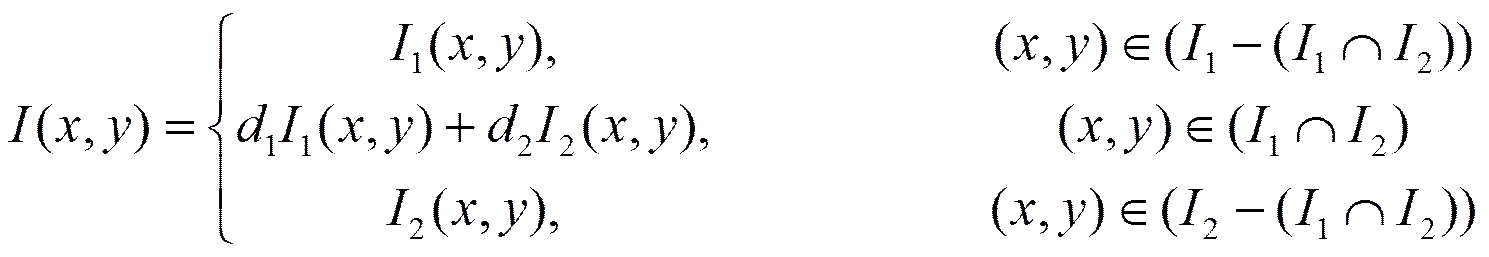
参数，与重叠区域的宽度有关，且+= 1，0<,<1。在重叠区域中由1渐变到0，由0渐变到1，如图1(a)所示（实线为，虚线为），由此实现了在重叠区域中由到的缓慢平滑过渡。该方法在拼接图像序列的重叠区域存在图像空间位置不一致，特别是存在运动物体时会出现很明显的重影和鬼影现象，为此作者改进该算法，对权值、引入带有余弦关系变换的函数，其中==,，的值由重叠区域的每一行的宽度确定，初值为0。假设某一行重叠区域的宽度为，则，该行重叠区域从左向右随着像素位置递增。由图1(b)可以看出（实线为，虚线为），在重叠区域中权重，减小与增加的速度均较0-1渐变要缓和，这样就保证了在重叠区域中线左侧参考图像的权重更大一些，在中线右侧拼接图像的权重更大一些，从而有效地减少了靠近重叠区域左右边缘处的重影和鬼影现象。将融合后的图像作为与图像再次使用该方法进行加权融合，以加重在拼接图像中的权重，以此来消除重叠区域中线周围的重影与鬼影现象。

(a)0-1渐变权重函数

(b)　余弦关系渐变权重函数

6　实验结果及性能分析

为验证算法的有效性，以两幅图像进行实验。实验条件：英特尔迅驰双核1.87G，2G，MATLAB6.5，WINXP，SONY170。使用的图像是通过手持相机，以固定焦距连续拍摄的大小为640´480´3，JPG格式的两幅图像，如图2所示。利用EMD对和分别进行分解，获得固有模态函数，和，，其中和分别为对应于的第一个固有模态函数和第二个固有模态函数，和是对应于的前两个固有模态函数，如图3(a)~(d)所示。图3(e)为与的叠加，图3(f)为与的叠加。图4(a)、(b)是对和分别进行Harris角点检测，并按照角点响应值由大到小提取的前200个特征点。使用归一化相关系数法对提取的特征点在与上进行匹配，相关窗口大小为13×13，匹配点对如图4(c)、图4(d)所示。该实验的部分实验数据与对获取的原始图像与直接进行特征点提取与特征点匹配操作的实验数据如表1 所示，表1中还同时列出了本文实验3（实验用图为图8(a)与图8(b)）的一组实验数据，通过对比可以看出基于EMD的特征点匹配的正确率高于基于原图像的特征点匹配的正确率。图5为使用0-1渐变加权平均融合法得到的融合图像，从图中可以看出有明显的重影与鬼影现象（由方框框出）。图6为使用基于余弦关系变换的加权融合算法得到的融合图像，从两幅图像的对比中可以看出该方法可有效去除重影与鬼影。图6为待拼接图像的重叠区域超过50%的拼接效果图，图7、图8是使本文方法得到的另两组重叠区域少于50%的实验2与实验3的拼接效果图。（注：在图像拼接过程中，由于图像的旋转和平移会产生部分黑色边框，在本文的实验中为了保持图像信息的完整性，没有对边框进行切割。）

(a)的第1个固有模态函数(b)的第2个固有模态函数(c)的第1个固有模态函数

(d)的第2个固有模态函数(e)与的叠加(f )与的叠加

图3 经EMD分解的固有模态函数及其叠加的图像

(a)对进行Harris角点提取(b)对进行Harris角点提取

(c)(d)使用归一化相关系数法得到的匹配点对

图4 对与进行特征点提取与特征点匹配

表1 基于EMD的特征点匹配与基于原图的特征点匹配效果比较

（注：表1两组实验是在相同的实验条件下进行的，实验条件如上文所述。）

图5　0-1渐变加权平均融合后的拼接图

图6　基于余弦关系变换加权融合后的拼接图

(a)实验2左图

(b)实验2右图

(c) 实验2拼接效果图

(a)实验3左图

(b)实验3右图

(c) 实验3拼接效果图

7　结 论

本文研究了角点检测，特征点匹配、变换矩阵估计、图像配准与融合等有关图像拼接的关键技术，提出了一种基于EMD的图像拼接技术，通过实验证明了该方法有效提高了特征点匹配的正确率，具有很强的自适应性与鲁棒性，在图像融合方面提出了一种基于余弦关系变换加权融合算法，通过实验表明该方法能够实现视觉上的自然过渡和无缝拼接，并克服了传统0-1渐变加权融合算法在图像重叠区域产生的重影和鬼影现象，具有很强的实用性。

[1] Harris C G, Stephen M. A combined corner and edge detector [C]//Proc. 4Alvey Vision Conference, Manchester, 1988: 147-151.

[2] Huang N E. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [C]//Proc. of the Royal Society of London, 1998: 903-995.

[3] 孙 晖. 经验模态分解理论与应用研究[D]. 杭州: 浙江大学, 2005.

[4] 田 丹, 高 强, 赵振兵, 等. 基于经验模式分解和互信息的图像配准研究[J]. 电力系统通信, 2009, 30(195): 37-40.

[5] Nunes J C, Guyot S, Delechelle E. Texture analysis based on local analysis of the bidimensional empirieal mode decomposition [J]. Machine Vision and Applications, 2005, 16(3): 177-188.

[6] Stefano L Di, Mattoccia S, Mola M. An efficient algorithm for exhaustive template matching based on normalized cross correlation [C]//Proc. 12International Conference on Image Analysis and Processing, 2003: 322-327.

[7] 周亚平. 图像配准技术研究[D]. 杭州: 浙江大学, 2008.

[8] ZHAO Xiangyang, DU Limin. An automatic and robust image mosaic algorithm [J]. Journal of Image and Graphics,2004, 9(4): 417-422.

[9] 黄有群, 付 裕, 马广焜. 基于RANSAC算法的柱面全景图拼接方法[J]. 沈阳工业大学学报, 2008, 30(4): 461-465.

[10] 顾费勇. 基于图像的自适应图像拼接算法研究[D]. 杭州: 浙江大学, 2008.

[11] Richard Szeliski. Video mosaics for virtual environments [J]. IEEE Computer Graphics and Applications, 1996, 16(2): 22-30.

[12] 仵建宁, 郭宝龙, 冯宗哲. 一种基于兴趣点匹配的图像拼接方法[J]. 计算机应用, 2006, 26(3): 610-612.

Image Stitching Based on Empirical Mode Decomposition

ZHANG Xiao-yu, DAI Fang, GAN Ming-hui, WANG Sai-fang

( College of Science, Xi'an University of Technology, Xi’an Shaanxi 710054, China )

The first two intrinsic mode functions of each image are obtained by using empirical mode decomposition algorithm to decompose images which need stitch. Through this method, the feature points are extracted and matched from the first two intrinsic mode function’s superimposition of each image. Based on these matched feature points pairs, parameters of the transformation matrix are calculated and then images are stitched. Experimental results have shown that this method effectively improves the accuracy rate of the feature points matched and has strong robustness. On image fusion, a novel weighed technique based on cosine relationship transform is proposed. With this technique, not only the seamless stitching images can be obtained, but also the phenomenon of ghosting in the overlapping stitching region can be eliminated.

computer application; image stitching; empirical mode decomposition; cosine relationship transform

TP 391

A

1003-0158(2011)01-0059-08

2009-06-22

陕西省教育厅科学研究计划资助项目（09JK611）；西安理工大学科技创新计划资助项目（108-210811）；西安理工大学校博 士启动金（108-210905）

张晓宇（1980-），女，山东商河人，硕士研究生，主要研究方向为计算智能与信息处理。