基于等效面积法的蜂窝梁挠度计算方法研究

2011-07-25李鹏飞王新敏

石家庄铁道大学学报(自然科学版) 2011年3期

李鹏飞，王新敏，袁泉，郭猛

(1.北京交通大学土木建筑工程学院，北京100044;

2.石家庄铁道大学大型结构健康诊断与控制研究所，河北石家庄050043)

0 引言

蜂窝梁是在工字钢或H型钢腹板上按一定的线形进行切割后变换位置重新焊接组合而形成的新型钢梁，其腹板上开孔形状最常用的为六边形或圆形。由于其自身的结构特点，与原型钢梁相比，蜂窝梁扩大了构件截面高度，在承载力相同的情况下蜂窝梁能够节约钢材25%～30%，节省油漆和运输安装费用1/3～1/6，同时蜂窝梁质量轻吊装方便［1］。除此之外，由于蜂窝梁腹板上开孔，可供供电、供热、制冷等管道通过，这样就能够有效地利用蜂窝梁腹板高度范围的空间，从而降低建筑高度。基于以上特点，蜂窝梁在工业厂房、民用建筑、机械、船舶等领域得到了广泛的应用［2］。

蜂窝梁最早起源于英国，发达国家在蜂窝梁的计算理论研究和应用方面起步较早。前西德早在DIN1086规范中就制定扩大比为1.5的蜂窝梁标准，英国亦编制了扩大比为1.5的各种型钢蜂窝梁的截面特性表格，日本也已经把蜂窝梁的设计纳入了设计规范［3］。在我国蜂窝梁的研究起步较晚，20世纪80年代初，冶金部建筑研究总院、重庆钢铁设计研究院和首都钢铁设计院等单位分别著文介绍国外蜂窝梁的试验研究成果及其推荐的计算方法［4］。

蜂窝梁由于腹板开孔，由剪力引起的腹板剪切变形较大，同时剪力次弯矩也对蜂窝梁的挠度产生影响，因此与实腹梁的计算方法不同，计算蜂窝梁的挠度时需要考虑剪力的影响，其计算分析过程比较复杂。对于蜂窝梁挠度的计算，至今仍没有简便而精确的方法。目前计算蜂窝梁挠度主要有三种方法［5-6］:①估算法，即以“当量实腹梁”的弯曲挠度乘以给定的增大系数来计算。各国给出的增大系数各有不同，美国(1.1～1.3)、俄罗斯(1.1～1.2)、德国(1.2～1.3)。此方法没有考虑蜂窝梁开孔形式、荷载形式等影响，有较大的局限性，误差较大。②精确的挠度计算方法，根据蜂窝梁结构特点，可以分别采取费氏空腹桁架分析法、变截面刚架计算方法、有交叉腹杆的空腹桁架计算方法等。③有限元方法，随着有限元分析方法的提出和计算机技术的进步，用有限元分析软件对蜂窝梁的挠度进行计算其精确度较高，可用于衡量各种计算方法精确度。但是有限元方法实现比较复杂，不易被广泛掌握。因此，研究蜂窝梁挠度较精确的简化计算方法对于推广蜂窝梁的应用，改进和制定相应的规范条文仍然具有重要的意义。

1 基于费氏空腹桁架理论的蜂窝梁挠度计算

根据结构力学中单位力法的分析方法，静定线弹性结构在荷载作用下的位移可以表示为

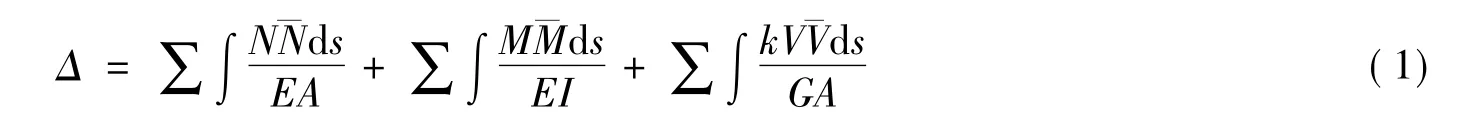
根据蜂窝梁受剪力影响大的受力特点，Allftlish等把蜂窝梁比拟为空腹桁架，为蜂窝梁挠度的计算提供了一个很好的概念模型和理论分析方法，该方法考虑了由于蜂窝梁腹板开孔造成的较大削弱，计算挠度时不但考虑弯矩的影响，而且需要考虑剪力的影响。一方面剪力造成蜂窝梁的剪切变形，另一方面剪力次弯矩造成梁桥的变形［7］。因此蜂窝梁的挠度包含弯曲挠度fM、剪切挠度fV和剪力次弯矩引起的挠度fc三部分

式(2)为蜂窝梁挠度的精确计算公式，只要分别求出式中各项，则蜂窝梁的挠度就能够得出。文献［8］中根据开孔长度等于孔净距的矩形孔蜂窝梁受纯弯作用的计算模型说明了蜂窝梁挠度的精确计算过程，该方法没有考虑开孔形式和开孔间距的影响，近似程度过大难免产生较大误差。本文提出以蜂窝梁的孔高比(开孔高度与梁高的比)d/h和距高比(开孔间距与梁高的比)s/h为变量，考虑不同开孔高度和开孔间距的影响并根据体积和惯性矩相等原则，分段取实腹梁截面和空腹梁截面各自的刚度计算挠度，提出蜂窝梁挠度的精确计算方法，说明基于费氏空腹桁架理论的蜂窝梁挠度计算原理和推导过程，为进一步对蜂窝梁挠度计算方法的改进奠定理论基础。

根据孔高比和距高比的定义，当蜂窝梁的高跨比一定时只要确定蜂窝梁的孔高比和距高比就能够确定蜂窝梁的开孔形式。以等边六边形开孔蜂窝梁为例，腹板高度为hw，腹板厚度tw，开孔高度d，开孔间距s，如图1所示。按面积和惯性矩等效的原则将蜂窝梁开孔部分腹板等效为矩形开孔腹板，开孔等效高度d1=3d/4，开孔长度D=

定义蜂窝梁矩形开孔空腹部分截面的等效惯性矩为I1，实腹部分的截面惯性矩为I0，与蜂窝梁尺寸相同的实腹梁称为当量实腹梁，其惯性矩为I0。蜂窝梁一个开孔和一个实腹部分称为一个单元，长度l1=D+s。蜂窝梁矩形开孔部分截面的等效惯性矩为I1=I0－

简支蜂窝梁腹板开孔如图1所示。假定全梁共分成n个单元，第n个开孔边缘距梁端的距离xn=ns+(n－1)2蜂窝梁实腹部分截面惯性矩为I0，开孔截面等效惯性矩为I1。所以在全梁范围内，蜂窝梁截面刚度可以表示为EI(x)。

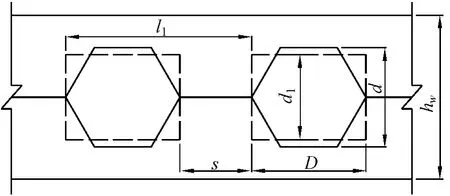
图1 蜂窝梁腹板开孔尺寸

当xn≤x≤xn+时，η=I0/I1－1，当xn－s≤x≤xn时，η=0。

根据单位荷载法，只考虑弯矩作用时蜂窝梁跨中挠度的计算公式为

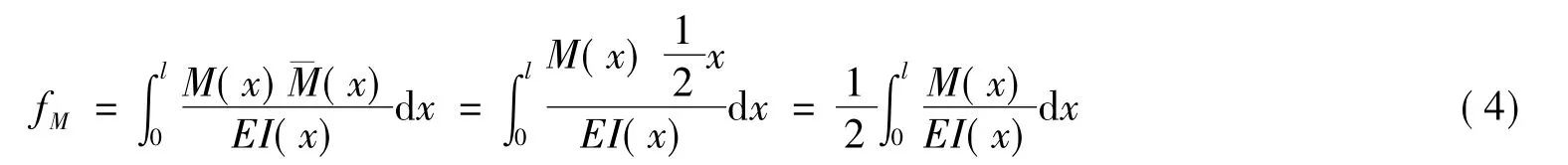
将I(x)的表达式带入式(4)，根据蜂窝梁的各段刚度不同的特点分段积分求和可得

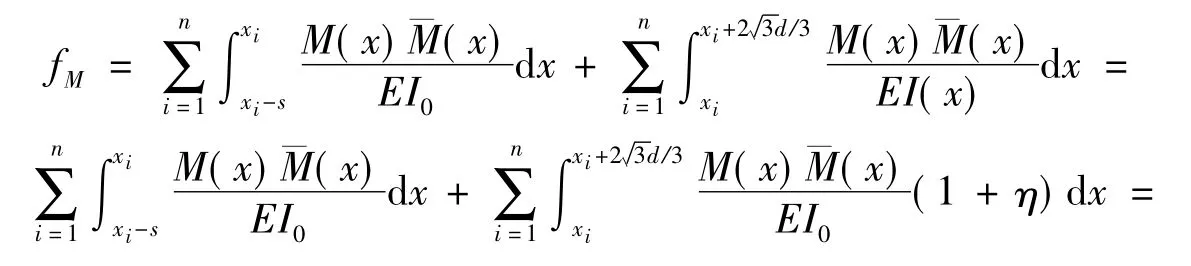
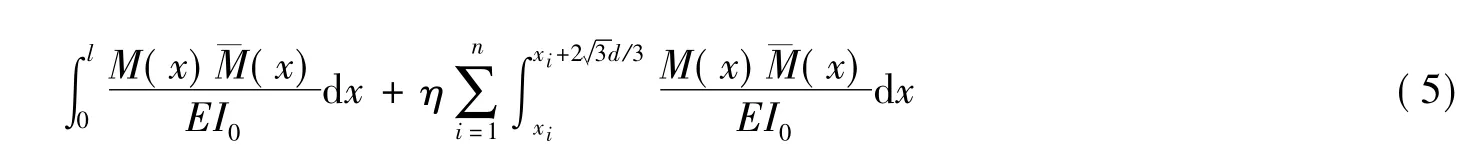
蜂窝梁开孔沿梁全长均匀分布，开孔部分长度占梁全长的比例为，因此fM近似表示为

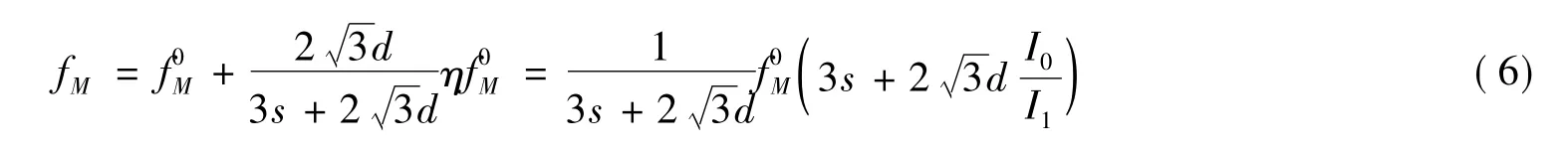
同理利用单位荷载法计算剪切挠度fV，蜂窝梁开孔部分截面的等效截面积为A1，实腹部分截面积即当量实腹梁截面面积为A0，如图1所示。蜂窝梁沿梁全长的截面积表达式为

当xn≤x≤xn+时，η=A0/A1－1，当xn－s≤x≤xn时，η=0。

蜂窝梁跨中的剪切挠度计算公式为

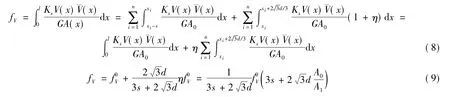
蜂窝梁腹板开孔对截面造成较大削弱，梁桥中所受的剪力在蜂窝梁的开孔部分产生剪力次弯矩，由剪力次弯矩引起的挠度fc也是影响蜂窝梁挠度的一个主要因素［9］。以图1所示蜂窝梁为例，假设第i单元梁桥跨中所受的剪力为Vi，梁桥跨中剪力次弯矩引起的挠度fc是由梁桥在剪力次弯矩作用下的弯曲变形fic'和剪力次弯矩作用下梁墩转动引起的挠度fic″组成的，如图2所示。

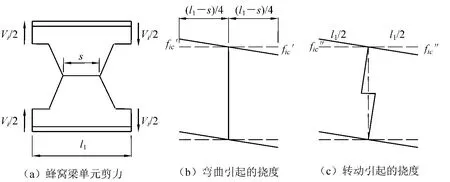
图2 剪力次弯矩产生的挠度

如图2(b)所示，跨中剪力作用下梁桥的弯曲挠度fic'为

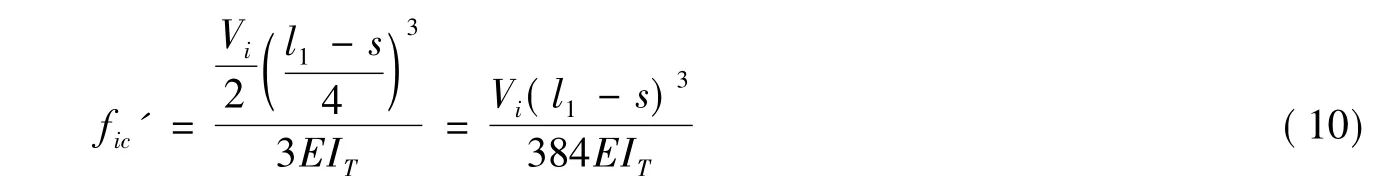
如图2(c)所示，梁桥跨中剪力作用下墩腰的转角θ以及墩腰转动产生的梁桥跨中挠度fic″为

因此，单元i中剪力次弯矩引起的梁桥跨中挠度为

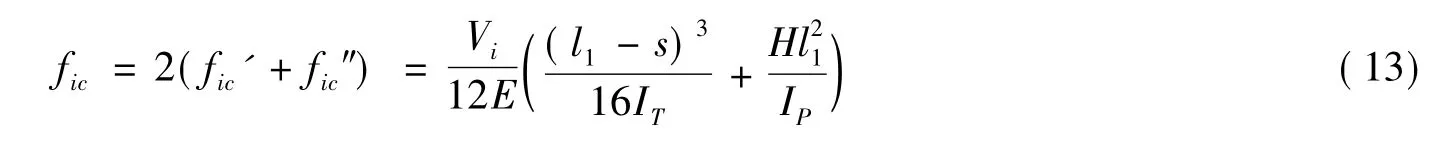
梁全长范围内剪力次弯矩引起的蜂窝梁跨中挠度为

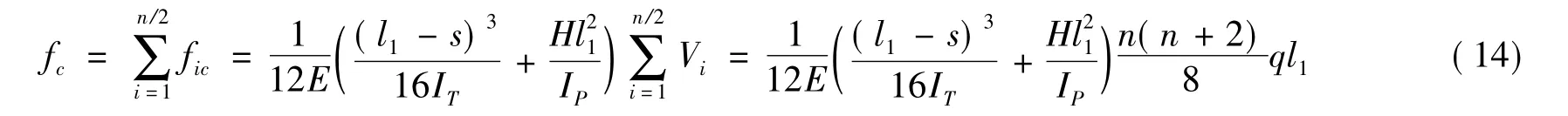
式中，l1为蜂窝梁的单元长度;IT为梁桥T形截面绕自身形心轴的惯性矩;IP为梁墩的等效惯性矩，IP=/48，g为刚度系数，近似取17.34［5］;Vi为蜂窝梁第i单元蜂窝孔中点承受的剪力;n为蜂窝梁的单元数;H为蜂窝梁的高度。

蜂窝梁的挠度精确计算公式可以写为弯矩引起的挠度、剪力引起的挠度和剪力次弯矩引起的挠度之和

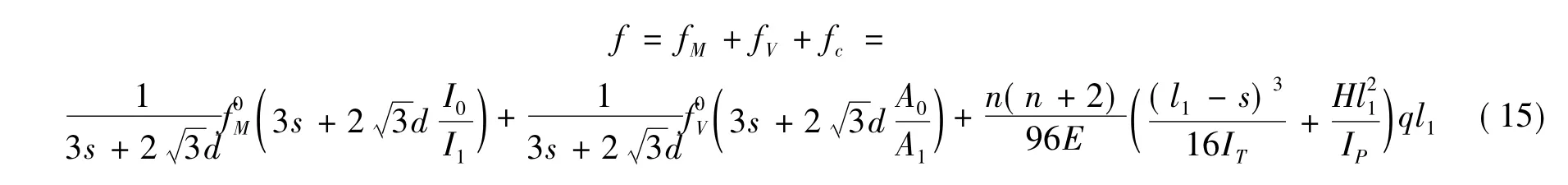
式(15)中考虑了蜂窝梁开孔高度d和开孔间距s的影响，因此该挠度计算公式适用于不同开孔形式和不同荷载形式。

2 算例分析

以某简支蜂窝梁为例，梁跨度L=6 m，截面高度取为H=300 mm，翼缘宽度b=200 mm，翼缘厚度t=12 mm，腹板厚度tw=8 mm，钢材采用Q345钢。梁上翼缘作用均布荷载q=10 kN/m，以蜂窝梁的孔高比d/H和距高比s/H为变量改变孔洞大小和间距，利用公式(15)分别对不同开孔状况的蜂窝梁进行挠度计算，梁的基本参数见表1。

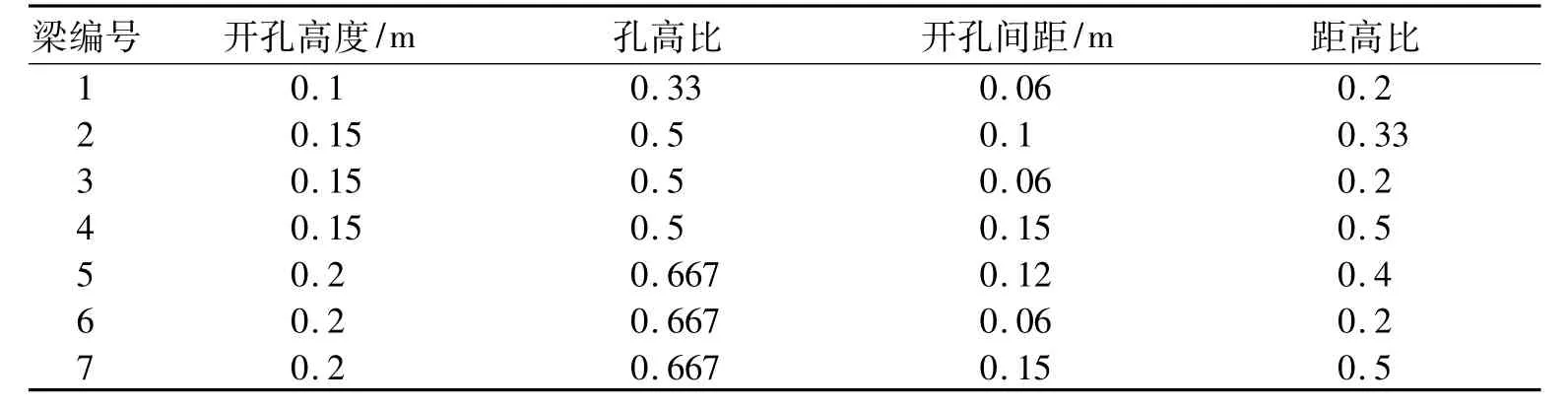
表1 蜂窝梁的基本参数

将利用公式(15)计算所得蜂窝梁的公式中各项挠度与蜂窝梁跨中挠度计算值列于表2中，有限元分析结果用于与计算结果对比以验证计算公式的准确性。

考虑到开孔过大对蜂窝梁的不利影响，蜂窝梁常见的孔高比为0.5～0.7之间，由梁1～4计算结果可以看出，由本文提出的挠度计算公式所得计算结果与有限元分析结果误差在5%以内，具有很高的精度。此外，当蜂窝梁的孔高比小于0.6时，由剪力次弯矩引起的挠度在蜂窝梁的挠度中所占比例十分小，因此在孔高比小于0.6时，可以忽略剪力次弯矩引起的挠度，进一步简化蜂窝梁的挠度计算公式为f=fM+fc。从不同孔高比的计算结果可以看出，当孔高比增大时，剪力次弯矩引起的挠度在挠度中所占的比例逐渐增大，所以当孔高比大于0.6以后，蜂窝梁挠度计算公式如式(15)所示，此时的计算公式中不能忽略剪力次弯矩的影响。

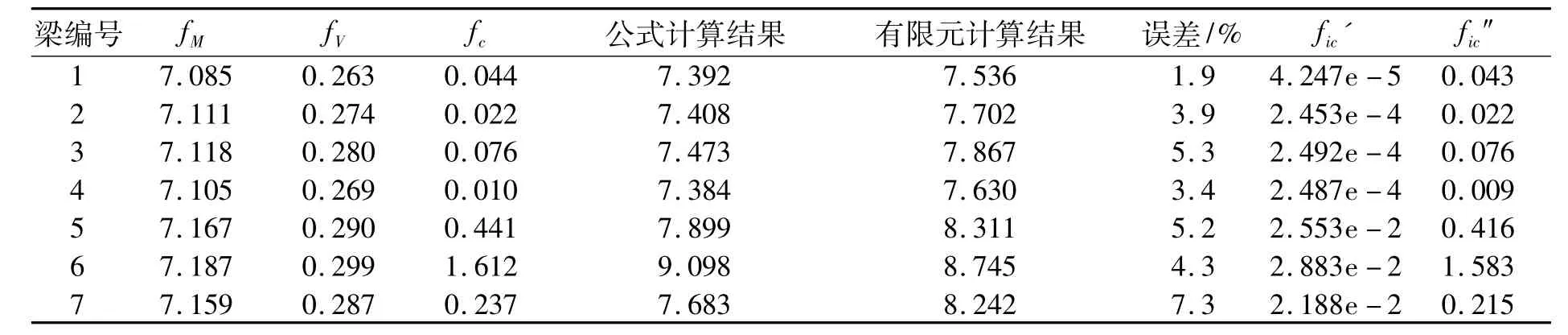
表2 蜂窝梁的挠度计算结果mm

从表1中梁5～7的计算结果可以看出，在剪力次弯矩中引起的挠度fc中，由墩腰转动产生的挠度fic″占fc的主要部分，梁桥弯曲产生的挠度fic'只占很小部分。开孔间距是剪力次弯矩产生的挠度的主要影响因素，根据梁5～7的计算结果，当孔高比一定的情况下，随着距高比的减小，梁墩的等效惯性矩IP逐渐减小，墩腰转动产生的挠度逐渐增大，剪力次弯矩引起的挠度fc也随之增大，成为蜂窝梁挠度的主要影响因素。因此在蜂窝梁的设计中，应该保证开孔之间有足够的梁墩宽度，以减小因为腹板过分削弱而产生的剪力次弯矩效应。

综上所述，本文提出的蜂窝梁挠度计算公式考虑了孔高比和距高比的影响，计算精度满足工程实际需求，可用于蜂窝梁的挠度计算。