克服电容式电压互感器暂态超越的新方法

温荣，杨波

(1.广西电网公司柳州供电局，广西 柳州 545005;2.广西电力职业技术学院，广西 南宁530007)

1 引言

由于电容式电压互感器(CVT)造价低廉、具有电磁式电压互感器的全部功能，同时可兼作载波通信的耦合电容器之用，不存在铁磁谐振问题的优点而被广泛应用于高压和超高压电网中［1］。然而当系统发生故障时，CVT由于其内部结构及参数特性，二次信号发生严重的暂态过程，导致距离保护I段的超越。为解决此问题，国内外展开了大量研究，主要方法有［2－4］:缩小保护范围或延时动作;根据 CVT参数估计误差并进行二次电压补偿;根据电源阻抗比(SIR)估计误差大小，延时动作。

以上方法需要预先知道CVT的内部参数及负载情况，而实际上，CVT的内部参数并不总能得到，且CVT的负载随着二次设备的投退，无法事先确定;缩小保护范围及延时动作在一定程度上能够有效防止距离保护的暂态超越，但保护的灵敏性和速动性受到极大的限制，特别不利于高压电网系统的安全与稳定运行。因此，探索适合微机保护的新方法克服CVT暂态超越，提高距离保护的动作速度，具有实用意义。

本文提出一种改进的全波傅氏算法与改进半波傅氏算法相配合的新方法，该方法不需要知道CVT的参数和负载。利用实时数字仿真(real time digital simulator，RTDS)工具进行仿真校验，结果论证了该方法的可行性和正确性。

2 CVT的暂态过程

CVT由分压电容、补偿电抗器、中压变压器、阻尼器等部分组成，如图1所示，Ce为等效分压电容;L1为补偿电感和中压变压器的漏感之和;R1为相应的电阻;Rf、Cf、Lf和rf为谐振型阻尼器的参数;Lb和Rb为负载的电感和电阻。

图1 CVT等值电路图

由于CVT中存在多个储能元件，故障时会产生暂态过程。其故障暂态电压如图2和图3所示。

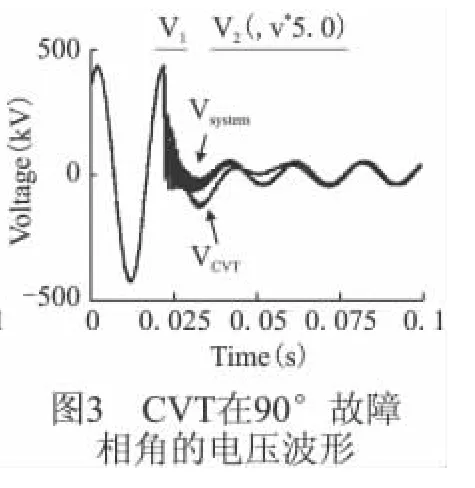
由图可以看出，故障发生在一次电压过零时的暂态影响最为严重，其故障暂态持续超过两个周波，暂态幅值甚至可达到正常电压水平的40%［5，6］。

在文献［7］和［8］中，已对CVT的暂态过程及其影响因素的关系进行了详尽的论述，在此只作简单的概括。内部参数对暂态过程的影响主要有:①等效分压电容Ce;②中压变压器一次侧电压(中压)Um;③谐振阻尼器阻尼电阻Rf;④谐振阻尼器谐振电容Cf。其中，Ce、Um、Rf的值越小，CVT 的暂态过程越严重，而Cf的情况则相反。

外部因素对CVT暂态的影响主要为:①负载参数(如负载容量、功率因数);②故障电压相角α。负载容量越大、功率因数越低，CVT的暂态越严重;故障电压相角α=0°时最为严重，α=90°时暂态最良好。此外，对于距离保护而言，电源阻抗比(SIR)越大，引起的CVT二次侧电压误差越大，保护就越容易发生超越动作。

通常故障后的CVT二次电压除基波电压外，含有多个非周期分量及衰减高频分量。CVT的输出电压表达式为［4］:

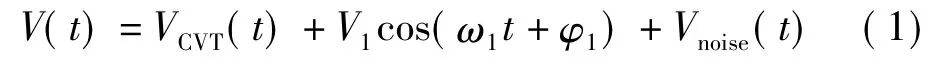
式中:V1、φ1分别为基波电压信号的幅值和初相角;Vnoise为包含衰减高频分量和高频谐波的噪音信号;VCVT为暂态电压信号，其通常的表达式为:

式(2)为含有4个衰减非周期分量的CVT二次电压，用于现代特高额定电容值的CVT;式(3)为含有一个衰减振荡分量和2个非周期分量的CVT信号，其用于普遍类型的CVT。无论对于哪种CVT类型，其暂态分量都是以非周期分量为主，图4为CVT的基波信号与暂态噪音信号的比较示意图。因此，克服距离保护暂态超越的关键在于克服CVT的暂态分量的影响。

图4 故障时CVT信号成分示意图

3 改进距离保护算法

3.1 改进傅氏算法

目前，微机距离保护通常采用傅氏算法获得基频电压和电流的向量，然后取两者的比值计算出测量阻抗来判断故障的区域。根据傅氏算法原理，全波傅氏算法的基频向量实部和虚部分别为:

式中:N为每周波采样点数。

同理，半波傅氏算法的实部和虚部分别为:

式中:N为每周波采样点数。

由于故障时CVT暂态信号中含有多个衰减非周期分量，为滤除这些分量，文献［9］提出了一种通过增加两个采样点的改进全波傅氏算法，现将该法引进到本文距离保护中并优化推广应用到全波及半波傅氏算法中。假设输入电压信号为式(1)，其中CVT的暂态信号取式(2)表示，取t∈［0，T］，则全波傅氏变换的基频电压的结果为:4

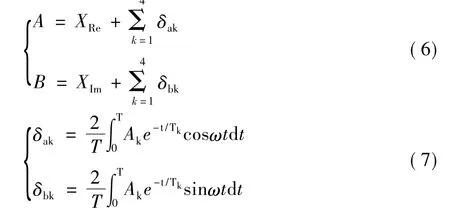
然后，取t∈［ΔT，T+ΔT］，ΔT为采样周期，即将第一个采样值去掉，在最后紧接着补上一个新采样值(此时采样序列从2到N+1)，全波傅氏变换得到

最后，再取t∈［2ΔT，T+2ΔT］，即去掉第 1、2 个采样值，在最后顺序补上2个新采样值(此时采样序列从3到N+2)，再进行全波傅氏变换得到:

由式(6)、(8)、(10)消去中间变量XRe、XIm、e－ΔT/Tk和e－2ΔT/Tk，可得

对于基频分量，ka、kb、k'a、k'b均为常量，将式(12)代入式(6)，即可得到实部和虚部:

由于半波傅氏算法［10］与全波傅氏算法仅在积分区间(数据窗长)上的区别，故以上的改进全波傅氏算法可应用推广到半波算法中，限于篇幅，具体公式略。

3.2 改进保护方案

上述的改进傅氏算法理论上能完全滤除衰减非周期分量，但由于傅氏算法本身是离散求和的方法，用离散值累加代替连续积分，其计算结果要受到采样频率的影响［11］，实际的采样装置决定了采样频率不能无限大，因此，算法与理论积分还是存在一定的误差，改进后的傅氏算法仍不能完全解决暂态超越问题。文献［12］采用了几种傅氏算法相配合的措施，引入了一个半周波的傅氏算法。本文改进的全波与半波算法，对CVT暂态时的计算结果有其自身特点，如图5所示。

图5反映了改进后的全波傅氏和半波傅氏算法在仿真0.03s发生故障时的计算结果。纵坐标为电压幅值，直线代表故障后达到稳态的实际电压(理想获得值)。由图可以看出，两种傅氏算法对CVT暂态的运算结果都有一定的超越(计算电压幅值小于实际值)，在超越开始点、超越持续时间及超越结束点都各自相异。最重要的信息是，两种算法出现超越的时刻大体上相互交叉，仅有极小部分为同时超越，利用这个特点，可以相互配合作为保护的动作判据。

图5 两种改进傅氏算法的暂态超越情况

文献［4］分析了1/8周波的短数据窗算法与全波傅氏算法的配合可以作为保护判据;然而，文献［13］指出，小矢量或短数据窗的快速算法对于故障后暂态过程的相量计算可能偏差较大，不适于距离保护等复杂相量计算的保护。对于长数据窗算法的应用，由于数据窗比较长，获得稳态的数据相对较多，有利于保护的正确判断，但保护的运算速度受到一定限制。大量仿真试验得出，采用改进的全波与半波傅氏算法相配合，能够兼顾保护动作的正确性与快速性。

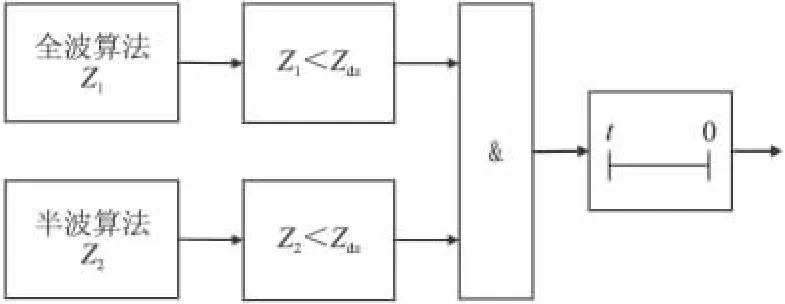
图6 保护逻辑图

改进的距离保护方案如图6所示。保护的动作逻辑由改进的全波算法和半波算法作为保护算法，分别与整定阻抗作比较后构成“与”门输出。通过大量仿真试验，本文考虑了保护在所以区内故障可靠动作和区外故障安全闭锁的原则，整定10ms作为保护的动作时间，这个时间完全符合距离保护I段的要求。

4 仿真分析

为验证本文保护方案的有效性，针对一个500kV系统利用RTDS进行了仿真试验，系统结构如图7所示。

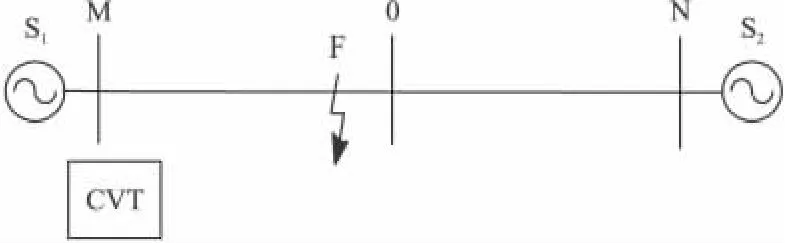
图7 仿真系统模型图

仿真具体参数如下:电源S1和S2等效系统参数均为R0=2.5Ω，L0=226mH，R1=7.5Ω，L1=783mH;线路MO和 NO的正序、零序参数分别为R1=0.0178Ω/km，L1=0.897mH/km，C1=0.0135μF/km，R0=0.1148Ω/km，L0=2.63mH/km，C0=0.0092μF/km，线路长度均取100km。保护装置和CVT安装在M侧，故障设在正向F点处。

本文采用方向圆动作特性的距离保护并假定测量电流为理想值，则测量阻抗的暂态过程即反映了CVT电压的暂态。保护算法的采样率为每周波24点［14，15］，在每个采样点对所有的保护算法和逻辑进行并行计算，使得仿真计算结果具有实时性，且可信度较高。

图8 区内与区外故障保护动作性能比较

将距离I段保护整定范围80%，图8反映了分别仿真线路60%(区内)和95%(区外)处故障的距离保护动作性能，图中由上至下的五个曲线分别表示:①传统保护的跳闸信号;②改进保护的跳闸信号;③传统保护的故障判断信号;④改进全波的故障判断信号;⑤改进半波的故障判断信号。本文的跳闸信号为当保护故障判断信号为高电平“1”并持续10ms时输出高电平(“1”表示出口跳闸)。可以看出，区外故障时，改进的保护算法有效克服了暂态超越。故障过程的测量阻抗轨迹如图9所示，故障点设在线路80%处，图9中的斜线代表全长线路阻抗，圆即为整定的方向圆，整定范围80%。

图9 各种算法的测量阻抗轨迹图

采用上述方案及参数构成仿真系统在RTDS上试验，以A相为特殊相研究，得到各种条件及各种类型下故障的距离保护I段的实际保护范围，结果如表1所示。

表1 各种故障条件的距离I段保护范围情况

表1的仿真结果表明，在相同的保护整定动作时间下，传统的距离保护范围大大超越了I段的整定值;接地故障要比相间故障的超越更为严重，这与理论分析结论相同(接地故障的电压降落更严重)。改进的保护方案在三相短路接地时的最严重暂态情况下，保护I段范围最大达到了86%，应该说其误差范围还是在能够接受的范围，基本满足保护“四性”的要求。上述仿真没有考虑过渡电阻，因为当有过渡电阻存在时，对保护防超越是有利的，仿真证实了这一点。

5 结论

CVT的暂态过程使得距离I段保护范围大大超越了下级线路，其暂态噪音是以衰减非周期分量为主。本文采用改进的全波与半波傅氏算法相配合的方案，与传统的保护算法相比较，改进的方法能克服CVT故障后的衰减非周期分量的影响，确保了保护范围。仿真结果表明，改进的保护方法确实有效地克服了暂态超越的影响，避免了为防止超越而牺牲宝贵的保护动作时间，符合保护速动性和可靠性的要求。此外，该方法不需知道CVT的各项参数，运算速度较高，应该有较大的实际应用价值。

［1］凌子恕.高压互感器技术手册［M］.北京:中国电力出版社，2005.

［2］李一泉，何奔腾，黄瀛.基于电容式电压互感器暂态误差估计的自适应距离保护［J］.中国电机工程学报，2004，24(10):72 －76.

［3］李一泉，何奔腾.基于PRONY算法的电容式电压互感器暂态基波辨识［J］.中国电机工程学报，2005，25(14):30 －34.

［4］索南加乐，谢静，刘东，等.克服距离保护暂态超越的新方法［J］.电力系统自动化，2006，30(10):52 －57.

［5］Bogdan Kasztenny，Dave Sharples，Vince Asaro，et al.Distance relays and capacitive voltage transformers－balancing speed and transient overreach［C］.53rd Annual Conference for Protective Relay Engineers，2000.

［6］Daqing Hou，Jeff Roberts.Capacitive voltage transformer:transient overreach concerns and solutions for distance relaying［C］.Electrical and Computer Engineering，1996.Canadian Conference on，1996，1(s):119 －125.

［7］任桂英，刘宗歧，郭家骥，等.电力系统故障时CVT响应的研究［J］.华北电力学院学报，1995，22(4):35 －40.

［8］郁惟镛，吴小建.电容式电压互感器暂态响应的数字仿真研究［J］.继电器，1998，26(1):27 －32.

［9］苏文辉，李钢.一种能滤去衰减直流分量的改进全波傅氏算法［J］.电力系统自动化，2002，26(23):42 －44.

［10］丁书文，张承学，龚庆武，等.半波傅氏算法的改进［J］.电力系统自动化，1999，23(5):18 －20.

［11］高婧，郑建勇，潘震东.电力系统微机保护中改进傅氏算法综合性能的研究［J］.继电器，2002，30(10):16 －20.

［12］张延鹏，李一泉，何奔腾.一种消除CVT暂态超越的新方法［J］.继电器，2005，33(13):1 －5.

［13］文明浩，陈德树.小矢量算法浅析［J］.电力系统自动化，2003，27(3):42－44.

［14］王爱玲，陈新南，刘捷，等.RCS－900系列保护装置与2048kbit/s复用通道时钟的配合［J］.电力系统自动化，2007，31(6):94－98.

［15］许建德，陆以群.新型数字电流差动保护装置中的数据采样同步和通信方式［J］.电力系统自动化，1993，17(4):23 －26.