基于参数估计的同杆双回单线故障测距

陈霖，梁志坚，谭建成

（广西大学电气工程学院，广西 南宁 530004）

1 前言

早期的输电线路普遍由单回线路构成。随着社会的发展，对电能的依赖越来越高。然而土地的日益紧缺，使得构建一条输电线路所需成本成倍增加。面对用电量的刚性需求与土地等建设成本增加的矛盾，同杆双回输电线路孕育而生。同杆双回输电线路由于所需的出线走廊窄，占地面积小，构建成本相对偏低，从而越来越多地被应用于电力系统中。然而，同杆线路之间由于互感的存在，传统的单回线路的故障测距算法并不完全适用于同杆双回线路中，故而需要研究新算法，以便适应双回线路故障测距的精度要求。

如何在具体应用中提高双端测距算法的测距精度，是当前国内外学者研究的一个重要内容。在已有的大多数双端测距算法中，线路参数都是作为已知量参与计算的。线路参数的准确与否，关系到测距算法最终结果的准确度，故而线路参数在测距算法中占有很重要的地位。当线路参数不准确时，测距结果会存在较大的测距误差。文献［1］经过仿真验证指出，线路参数给定值与实际路线参数不符是造成测距误差的一个重要原因。输电线路的线路参数一般都可以通过相关参数的计算获得，但在实际的运行过程中，由于受到周围环境等因素变化的影响，输电线路的参数并不是一成不变的，而是随着温度、气候、土壤等因素的变化而变化。文献［2］对线路长度变化的研究显示，由于线路长度在冬天和夏天的变化，也将对故障测距造成误差。本文为了消除因线路参数变化对故障测距精度的影响，提出一种基于参数估计的同杆双回路故障测距新算法。该算法原理上不受采样不同步角的影响，并能够有效的消除因线路参数造成的测距误差，实现在参数不准确或参数未知等情况下的精确测距。

2 同杆双回路的测距算法

2.1 六序分量法相模变换［3－5］

同杆双回线中，不但相间存在互感，线间也有互感的存在。这就给原有的测距算法带来了难度。而六序分量法能够较好地消除线间和相间互感。

本文假设每回线路的相间阻抗相等，两回线之间的线间互阻抗也相等。对同杆双回路采用六序分量法，将线间、相间均存在互感的双回路解耦成相互独立的序量，再用各序量对线路故障进行定位。对各相进行相模变换所采用的六序变换矩阵为:

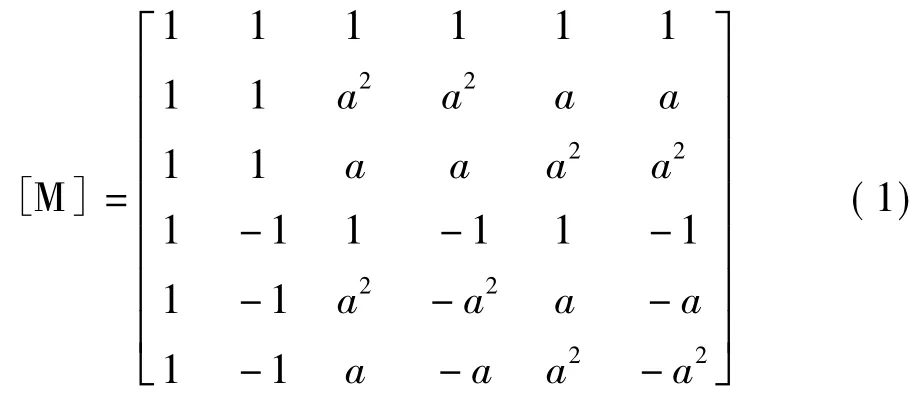
式中，a=ej120°，a2=e－j120°。相模之间的转换关系为:

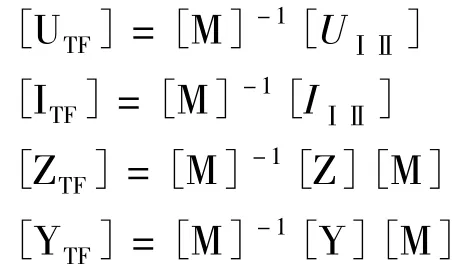
其中，［UTF］=［UT0UF0UT1UF1UT2UF2］T为电压的六序分量；［ITF］=［IT0IF0IT1IF1IT2IF2］T为电流的六序分量；［UⅠⅡ］=［UⅠAUⅠBUⅠCUⅡAUⅡBUⅡC］T为双回线的各相电压相量；［IⅠⅡ］=［IⅠAIⅠBIⅠCIⅡAIⅡBIⅡC］T为双回线的各相电流相量；［Z］、［ZTF］、［Y］、［YTF］分别为双回线的相、模阻抗矩阵和相、模导纳矩阵。下标A、B、C分别表示A、B、C三相；Ⅰ、Ⅱ分别表示第一回线和第二回线；T、F分别表示同向量与反向量。

2.2 最小二乘法简述［6］

最小二乘法是通过最小化误差的平方和寻找数据的最佳匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。

设有非线性方程

式中，x=（x1，x2，…，xn）T，i=1，2，…，m且m＞n。对于给定的数据点（xi，yi），由式（2）可列出一组方程，列出的方程个数m大于未知量个数n，在数学上称之为超定方程组。由于超定方程组得到的解会出现互相矛盾的现象，因此又称为矛盾方程组。矛盾方程组的求解通常采用最小二乘法。最小二乘法的基本原理就是要求函数中的yi=fi（x）参数x在最小二乘意义下的最佳估计值，也就是求使目标函数

为最小值时的参数x=（x1，x2，…，xn）T。由微积分理论知道Q取得最小值的充要条件是要求Q对参数x1，x2，…，xn求取的一阶偏导数为零，即

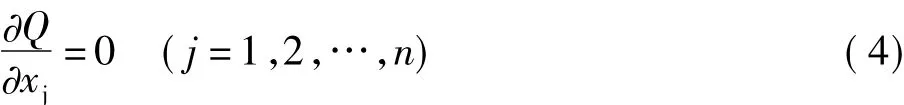
将式（3）在某一迭代点处附近按泰勒级数展开，并略去二次及二次以上的项后，代入式（4）中，并写成矩阵形式，得:

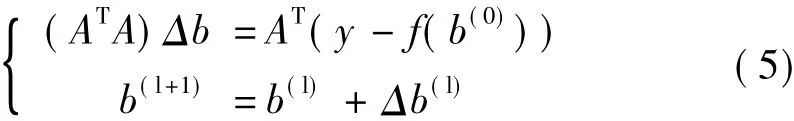
式中，Δb（l）是每次迭代修正量；A为非线性方程yi=fi（x）在b（l）处的Jacobi矩阵。

2.3 参数估计

根据基本电路传输线方程，利用故障前两端的电流和电压关系得到相关方程。

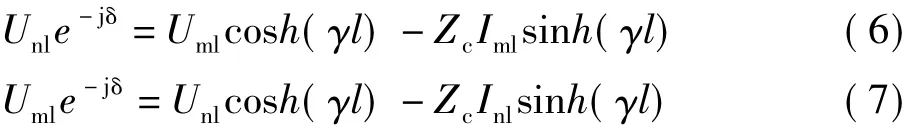
式中，电压、电流量是指某一独立模分量，下标1表示同向正序分量，γ为传播常数，Zc为波阻抗，δ为采样不同步角，l为线路长度。

根据基本电路传输方程分别从线路M、N两端推算出线路中点处的电压，利用线路上电压的延续性特性［7］，可得:

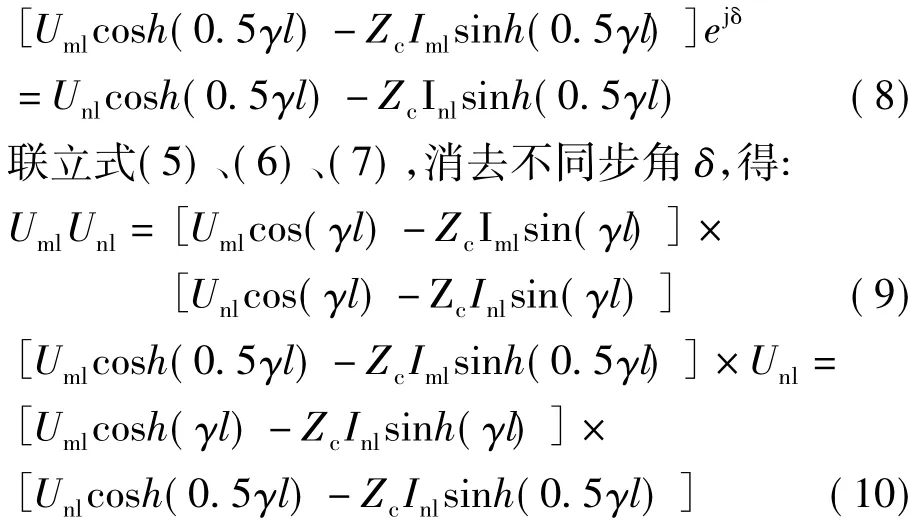
将（9）、（10）两式实部和虚部分解，得到一组关于传播常数γ的实部γ1、虚部γ2和波阻抗Zc的实部Z1、虚部Z2的四元非线性方程组:

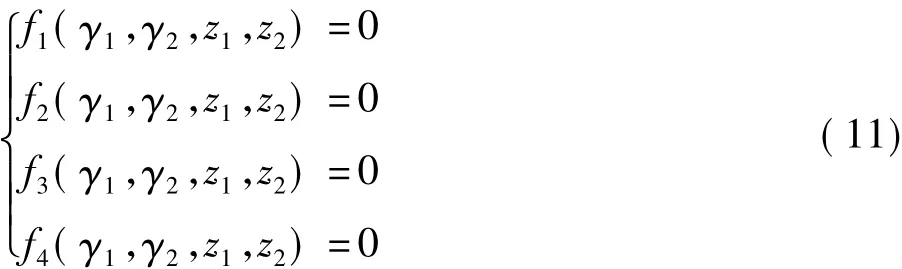
利用Matlab中求解方程最小二乘解的相关函数，得出最小二乘解。参数估计具体流程如图1所示。

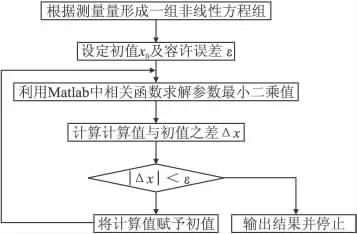
图1 参数估计流程图

2.4 故障定位

线路发生故障时，假设线路故障点为f，与M端的距离为x。根据故障后的电压、电流，可得:

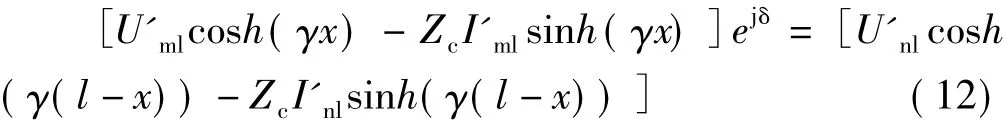
由式（6）、（12）可得:

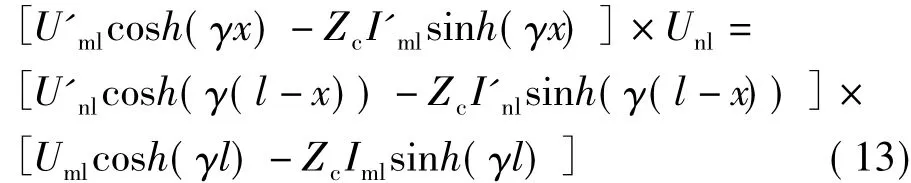
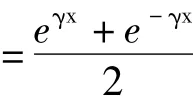
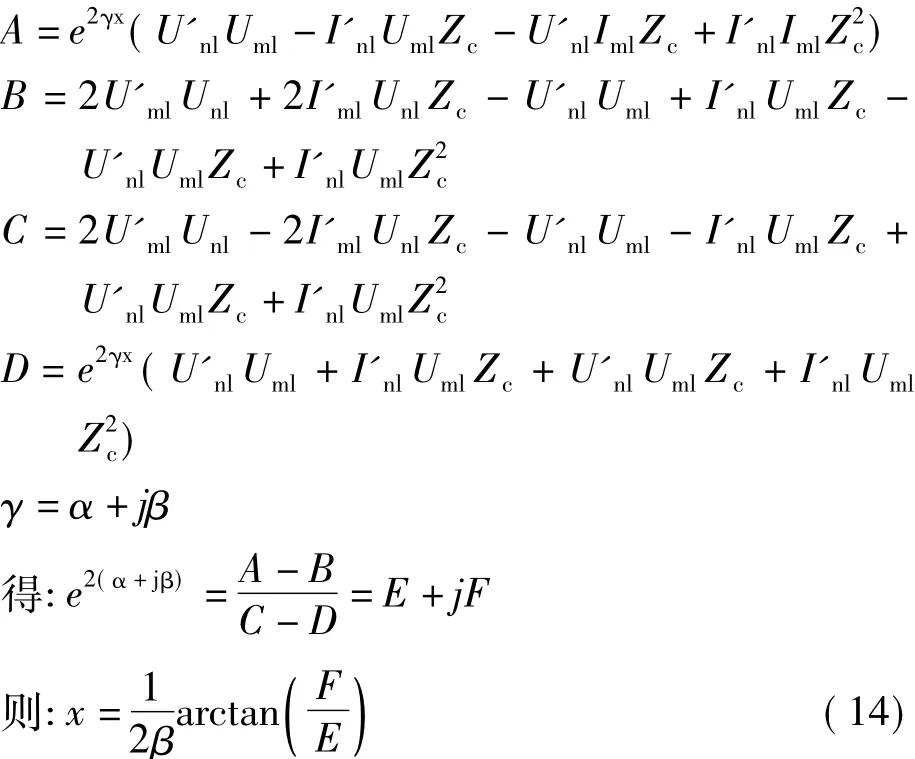
式（14）中，电压、电流为测量值，传播常数、波阻抗为参数估计值，解此方程即可求出故障距离。

3 算法验证

3.1 PSCAD仿真模型及参数

图2为本文采用的PSCAD仿真模型系统图，500kV电压等级双电源系统，线路全长300km。线路参数模型采用基于时域的贝瑞龙（Bergeron）分布参数模型。

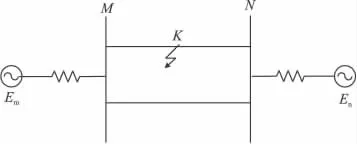
图2 仿真系统图

系统参数如下:

M端正序及零序阻抗为:Zm1=j69.999Ω，Zm0=j63Ω；

N端正序及零序阻抗为:Zn1=j69.998Ω，Zn0=j40Ω；

线路等效参数如下:

正序参数:R1=0.0363Ω/km，L1=1.6mH/km，C1=0.0105μF/km；

零序参数:R0=0.3796Ω/km，L0=4.2mH/km，C0=0.0146μF/km；

双回线间互阻抗参数为:r'=0.064Ω/km，

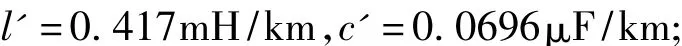
采样频率为20kHz，即每0.05ms采样一次。

3.2 仿真验证

同杆双回线故障区别于单回线故障的主要特点就是存在跨线故障，但在实际运行过程中，单回线路故障占总故障的比例在80%以上［8］，故而本文只对单回线故障的仿真结果进行研究。仿真实验中，对不同故障点、采样不同步角以及单回线不同故障类型进行了仿真实验。

测距相对误差采用以下公式计算:

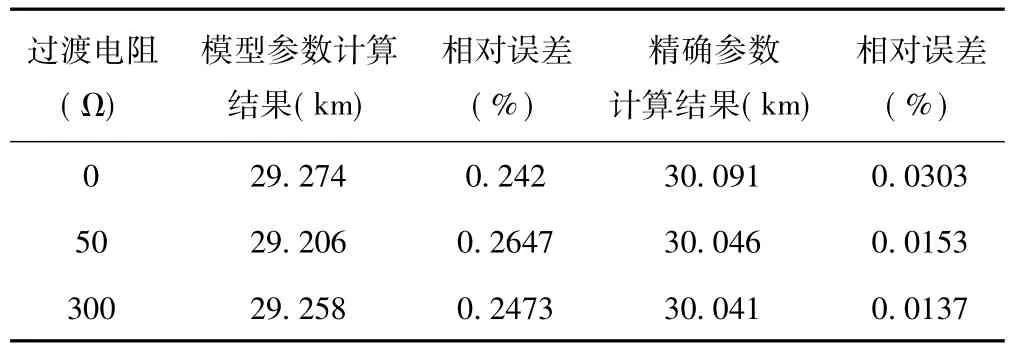
表1 δ=0°，x=30km时的单相接地测距结果

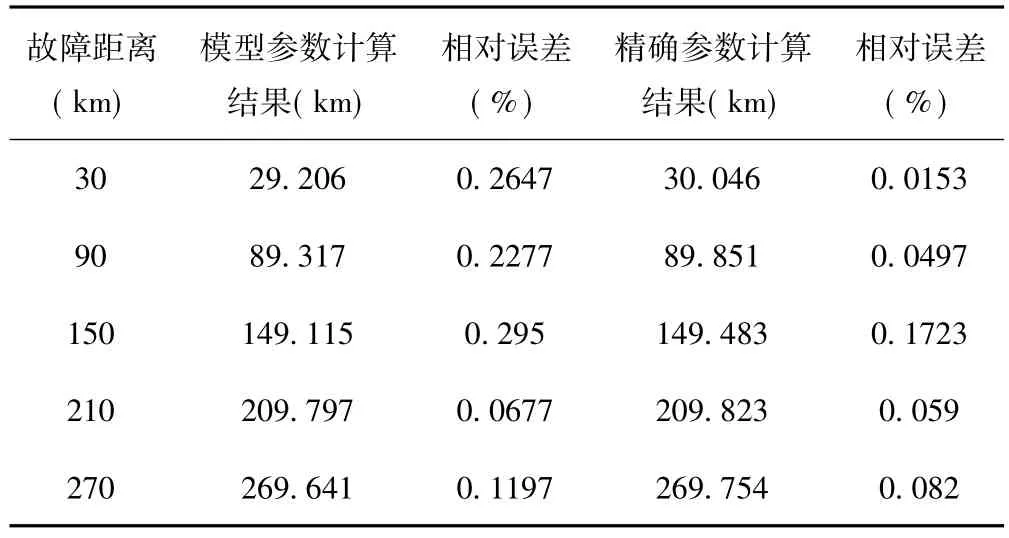
表2 δ=0°，Rf=50Ω时的单相接地测距结果

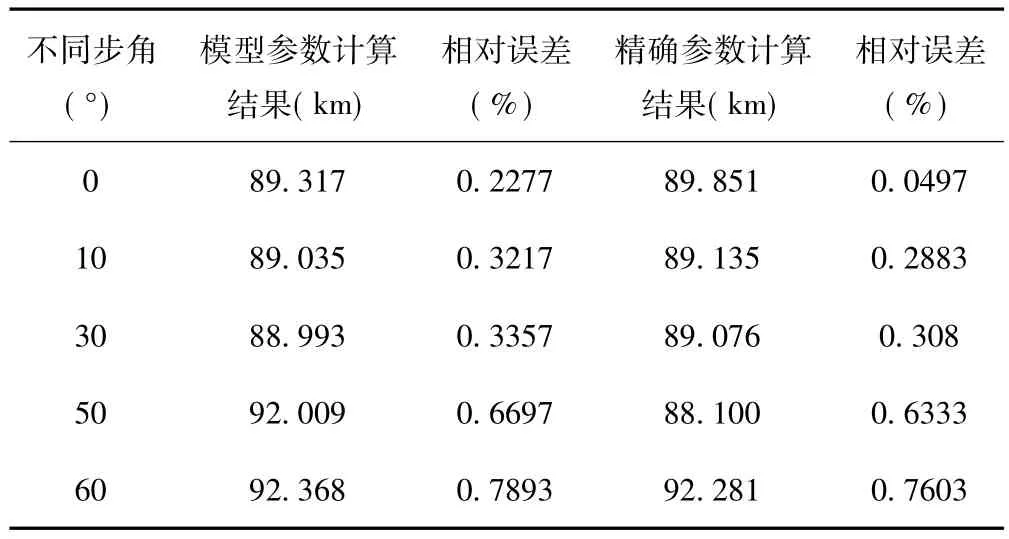
表3 x=90km，Rf=50Ω时的单相接地测距结果

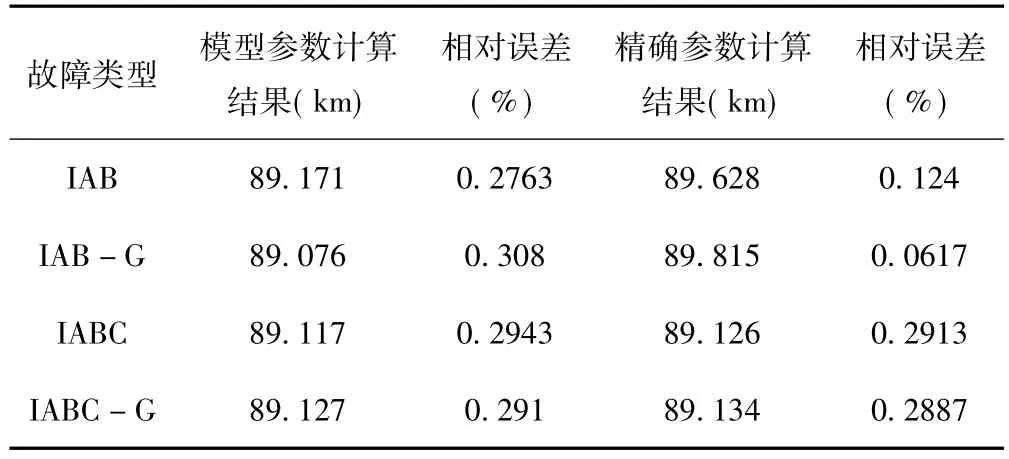
表4 x=90km，Rf=50Ω，δ=0°时的其他故障类型测距结果

从以上仿真数据表中所测数据可以看出，对于各种故障类型和各个故障位置发生故障时，计算结果精度都较高。其最大相对误差为0.7603%，最小为0.0137%，满足《全国电力调度系统“十一五”科技发展规划纲要》中对线路故障测距要求的综合误差不超过1%的要求。而且经过了参数估计的计算值比未经参数估计的计算均较精确，两者相差最高可达0.2463%，最小为0.0087%。算法中消除了采样不同步角的影响，但通过仿真结果可以看出，采样不同步角的增大，相对误差也相应的增加。故而需要进一步研究采样不同步角过大时对故障精度的影响。

4 结论

本文提出了一种基于参数估计的同杆双回路故障测距的算法，该算法具有:①采用了分布参数模型，并且对线路参数进行了一定的自适应校正，确保了故障测距在参数未知或不准确时的精度要求；②该算法基本不受不同步角、故障类型、系统运行方式的影响；③大量的仿真表明，该算法简单可靠，计算量小，易于实现，具有较高的应用价值。

［1］全玉生，王晓蓉，杨敏中，等.工频双端故障测距算法的鲁棒性问题和新算法研究［J］.电力系统自动化，2000，24（10）：28 －32.

［2］束洪春.基于分布参数线路模型的架空电力线故障测距方法研究［D］.哈尔滨：哈尔滨工业大学，1997.

［3］梁华为.高压同杆并架双回线故障测距误差修正算法的研究［D］.北京：华北电力大学，2005.

［4］梁军，麻常辉，等.基于线路参数估计的高压架空输电线路故障测距新算法［J］.电网技术，2004，28（4）：60 －631.

［5］朱声石.高压电网继电保护原理与技术［M］.北京：中国电力出版社，2005.

［6］刘钦圣.最小二乘问题计算方法［M］.北京：北京工业大学出版社，1989.

［7］陈铮.高压输电线路故障定位组合解决方案的研究［D］.北京：清华大学，2002.

［8］葛耀中.新型继电保护与故障测距原理与技术［M］.西安：西安交通大学出版社，2007.