基于免疫优势算法的配电网规划

周愈鹏，覃拓，危秋珍，蓝慧

（广西河池市供电局调度所，广西 河池 547000）

1 引言

长期以来，我国城市中低压配电网网络结构不合理，主要体现在网架结构薄弱，主次网架不清晰，多分段、多关联的网络联接未形成，造成了用户电压不稳定、网络损耗大、频繁发生故障等问题。根据2000年对全国286座城市的统计，我国中低压配电网的平均供电可靠性为99.887%，有80%的用户停电是由于配电网的问题引起的。因此，进行配电网规划优化配电网络网架结构，降低配网容量要求、网络损耗，减少建设资金投入和降低维护费用，对提高社会和电网公司的经济效益等具有重要意义［1］。

2 配电网规划算法

配电网优化规划问题实质上就是一个具有离散、不确定、多目标、多阶段的复杂系统的组合优化问题。目前，配电网规划的算法主要有数学优化规划方法和启发式优化规划方法。数学优化规划含线性规划法和模糊数学类的不确定性规划法，由于配电网规划是一个非常复杂的非线性规划问题，它是非可微性的，所以直接用传统的数学优化方法来进行配电网规划往往会出现迭代发散、收敛速度慢和难以得到比较准确的结果等问题。针对数学优化规划方法的不足，人们提出了启发式规划算法，它综合考虑了规划效率和规划效果两个指标，具有直观、灵活、计算速度快等突出优点，便于规划人员在规划过程中参与具体的决策，从而得出更符合工程实际的规划方案［2］。启发式规划方法有分为传统式启发方法即支路交换法、专家式启发方法、和现代启发式方法。目前应用现代启发式方法有神经网络、模拟退火法、蚁群最优化、遗传算法、免疫算法等。遗传算法是模仿生物进化过程的一种自适应随机搜索优化算法，由于其编码简单易行，且基于精英保留策略的遗传算法在理论上是一种全局收敛的算法，从而得到了较多的应用［3］。但在实际应用中，遗传算法仍有诸多不足，如种群多样性的丧失使算法有可能只收敛到局部最优，以及由于配电网辐射状的特点，使得遗传操作会产生不可行解［4］。为了解决上述问题，一些学者提出了改进的遗传算法，如文献［5］利用单亲遗传法获得了最优网架结构；同时，一些学者开始在遗传学基础上将免疫算子引入，提出了一种多种群免疫遗传算法来解决配电网规划问题，并取得了较好的效果，开启了利用免疫算法来进行配电网优化规划的途径［6］。文献［7］在保留遗传算法杂交、变异等因子基础上，提出了一种改进免疫算法的配电网规划，并采用信息熵理论来控制种群的多样性，以避免算法不成熟收敛，加快了算法的收敛速度。

本文在常规免疫算法的基础上提出一种免疫优势算法用于配电网规划。在树形编码的基础上，利用免疫机理对初始种群进行接种疫苗、利用免疫优势因子和改进的选择、变异、克隆等免疫操作来传统免疫算法进行改进，提高了种群的多样性，避免早熟收敛和加快算法收敛速度等，本文最后给出一个具体配电网规划的算例，以验证本文所提出的算法的有效性。

3 配电网规划的数学模型

其中:n为馈线总数；i为馈线支路编号；ci为馈线i的投资建设费用；χi该馈线i是否为新建，新建则为1，否则为0；ħi为馈线投资回收率；δi为馈线线i的年折旧率；α为单位电价；τmaxi为最大负荷利用小时数；ΔPi为馈线i的有功损耗。

上式服从如下条件约束:

①潮流约束AP=D

式中，A为节点—支路关联矩阵；P为馈线潮流向量；D为负荷向量。

②容量约束Pi≤Pimax

式中，Pi为馈线支路潮流；Pimax为该支路最大允许容量。

③电压降落约束Umin≤U≤Umax

本文配电网规划以年总费用最小为目标函数，包括建设投资费用、投资回收率、年折旧维护费用、运行费用（网损）其数学表达式是:

其中i=1，2，3……N，N为节点数

④辐射状网络约束

4 免疫优势算法的配电网规划

4.1 概述

免疫算法将求解问题的目标函数和约束条件对应于入侵生物体的抗原，最优问题的可行解对应于免疫系统产生的抗体，通过抗体和抗原的亲和度来描述可行解与最优解的逼近程度。

该免疫优势算法实际上就是一个通过克隆选择使群体的亲和度或适应度“成熟”的过程，即在克隆选择机制的作用下，不断地从群体中选择出一定数量的个体使之获得免疫优势，再对免疫优势个体进行克隆形成新的群体，判断新群体适应度是否符合要求，若不符合再通过变异等免疫基因操作，以产生越来越多的亲和度高的个体，如此循环直至群体亲和度逐步提高到一定水平。

4.2 接种疫苗

研究表明，对抗体进行接种疫苗，能有效地改进算法的性能。接种疫苗是指按照先验知识来修改个体的某些基因位上的基因，使所得个体以较大的概率具有更高的适应度。本文把配电网确定的打开开关的数目这一先验知识作为疫苗。在种群初始化时，先将抗体全部基因位设置为1，然后对每一个最小闭环注射一位0元素（这相当于把闭环打开），而注射的基因位是随机选取的。每个个体所注射0元素的总数，与确定的打开开关的数目相等。显然，这种方法能在很大程度上避免了采用随机初始化方法所产生大量的不可行解，获得的可行解占种群的比例更大。而对于产生的不可行解，可以使用下文的方法进行修复，使之成为可行解［8］。

4.3 抗体编码

本文在文献［9，10］的编码格式为基础经过改进得到了抗体的树形编码。假设某配网中有N个节点（编号从1～N），建立一个N阶方阵，方阵的行列号与节点编号相同，矩阵元素有0、1两种取值，用方阵来描述该配电网网络拓扑。矩阵元素aij的取值含义如下:矩阵元素a为“1”则相连，表示该矩阵元素对应的两节点i和j就有馈线支路相连接，自身节点矩阵元素为1；矩阵元素a为“0”则该矩阵元素对应的节点i和j没有直接的支路连接。例如，某辐射状配电网络有5个节点，接线示意图如图1。图2为该图对应的五阶方阵，节点与节点相连的则对应的矩阵元素为1，若节点间没有直接相连的则对应的矩阵元素值为0。

图1 辐射状配电网片断

图2 对应矩阵

4.4 适应度计算

在研究某个问题和现象时，其对应的结果总有个标准或机制来评价其优劣。本文免疫优势算法也和其他免疫算法一样，主要用亲和度或适应度函数对算法的解（抗体）进行评估。一般来说，算法的适应度函数Fit（f（x））是由目标函数f（x）转换而成的，由于本文的抗体目标函数为求最小化的问题，本文算法将式（1）的目标函数的倒数作为亲和度评估函数，c为控制常数，从而抗体（解）的亲和度越小，表明抗体（解）越优。

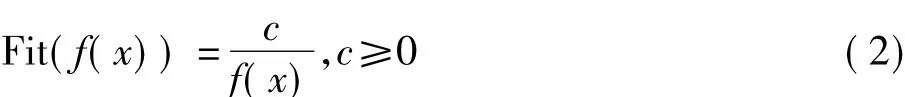
4.5 抗体免疫优势的获得与算法

由于抗体种群种的最优抗体与其他抗体相比，更能适应抗原的刺激，广义地讲，它具有免疫优势。因此，分析每次迭代中的最优抗体，从而获得免疫优势，使算法更具有通用性。基于上面思路，针对采用二进制编码的抗体种群，提出了如下的抗体免疫优势算子［11］。

记抗体群A=［a1，a1……an］为

定义参考抗体m=［m1，m2……ml］，其中

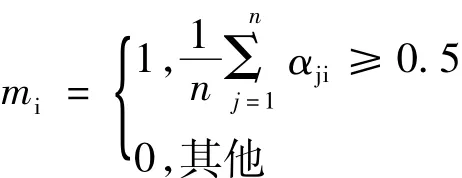
设αi∈A是抗体群中最好的抗体。若亲和度f（m） ＞f（ai），则互换。以一定概率Pd，使 αiєA，j=1，2，…，l并且在j≠i时该抗体获得免疫优势。其中，Pd是一个自适应调节参数，若f（a'j）＞f（aj）或f（m）＞f（ai）表明免疫优势的作用是有效的，则增大Pd，否则减小。具体地，令

H（·）是一门限函数，即

4.6 免疫操作

免疫基因操作主要包括克隆选择、交叉变异，它是免疫算法的核心操作，是产生新的优秀个体最主要的手段，也是保持群体多样性，避免早熟收敛的基础

（1）克隆选择

克隆选择过程是一个亲和度或适应度“成熟”的过程，即在克隆选择机制的作用下，不断地从群体中选择出一定数量的个体，并对它们进行克隆和变异等免疫基因操作，以产生越来越多的亲和度高的个体，直至群体亲和度逐步提高到一定水平。从上面可以看出，克隆选择的过程从本质上讲，它也是一个类似达尔文式的“优胜劣汰”的选择进化过程。本文的选择克隆是选择获得免疫优势的抗体，按照一定倍数进行克隆，以获得一个新的种群。

（2）交叉变异

本文在基于免疫优势算法的配电网规划具体实现中，交叉、变异操作是按与抗体亲和度或适应度成反比的概率从种群中选取个体来进行的。即亲和度越高的抗体被选中进行交叉、变异操作的概率就越低；反之，亲和度越低的抗体被选中进行交叉、变异操作的几率就越大，这样可以使种群中最优的部分个体能够在反复的免疫迭代过程中得以保存，而亲和度或适应度差的个体在反复的被交叉、变异亲和度不断提升直至达到要求。而已经确定选中进行交叉、变异的抗体，其交叉点是随机确定的，变异的基因位也随机确定的。至于整个群体中在每次迭代过程中有多少个体被选中进行免疫基因操作则由参数设置中的交叉率和变异率来决定。

4.6 算法的实现

（1）初始化参数设置。确定抗体编码长度L；k=0，生成初始规模为N0的初始抗体群落A（0）；设定算法参数，变异率为Pm，克隆倍数为Nk。

（2）抗体编码和接种疫苗。对种群中的抗体进行树形编码和接种疫苗。

（3）进化开始。根据式（1）的目标函数计算亲和度:A（k）。

（4）获得免疫优势。按文中方法获得免疫优势抗体群体Xk。

（5）依据设定的抗体克隆规模，进行选择克隆，获得新的抗体群落A（k+1）。

（6）抗体亲和度度量，并判断是否满足终止条件，是，则中止计算，输出结果；否则继续。

（7）对新抗体群落A（k+1）进行高频变异得到新的群落，并返回步骤（2）。

图3 免疫优势算法的计算程序的流程图

5 算例

本文所提出的免疫优势算法的配电网规划采用文献［10］中的配电网规划算例进行优化规划，该配电网共17个节点（含一个电源节点）。馈线投资回收率统一为ħ=0.1；馈线的年折旧率为δ=0.05；电价为α=0.5元/kW·h；最大负荷利用小时数为τmaxi=3000；该算例的抗体长L=17，种群规模N=100，免疫优势抗体种群规模M=20，抗体克隆倍数N=5c，交叉率Pm=0.4，变异率Pn=0.2，最大种群迭代终止代数tmax=100。

对于算例的应用，本文提出的免疫优势算法、文献［12］的常规免疫算法、文献［10］的改进单亲遗传算法进行配电网优化规划，得到的最优规划结果都一样，即最优规划支路为:{1，6，7，2，3}、{1，13，5，14}、{1，13，12，11，4}、{1，15，16，8，9，10}、{1，15，16，8，9，17}。在最优目标函数值即年总费用都为517.2（万元）的情况下，本文的免疫优势算法，不仅适应度曲线较好，而且收敛速度快。同时，按本文的优化方法运行三十次显示，最差的一次的迭代次数为31次，最好的一次的迭代次数为9次，大多数是迭代次数在20左右便得到了最优解。三种优化方法的平均迭代次数如表1所示，比较中可以看出，本文的免疫优势算法收敛速度和得到最优结果所需进化次数明显优于文献［10，12］。

表1 三种优化算法得到最优结果的平均迭代次数比较

6 结束语

本文详细介绍了免疫优势算法在配电网规划中的应用，在种群初始化和免疫补充时进行接种疫苗，通过修改个体基因上的某些基因位，对不可行解利用启发式进行修复，使之成为可行解，提高了计算效率，使得种群中可行解的比例增大；改进型树形编码保证了（抗体）配电网络的辐射性；抗体免疫优势因子的引入使抗体免疫优势则着眼于抗体本身上的独特型，对问题本身（抗原）依赖程度较低，可以不要需要依靠问题本身的先验知识，这让算法可以在线自适应动态地获得先验知识的体制，大大提高了算法的效率。而免疫克隆选择及变异再选择两算子利用大大加快了运算速度和有效地维持了种群的多样性，同时避免了算法早熟收敛。

［1］刘健，毕鹏翔，杨文宇，等.配电网理论及应用［M］.北京：中国水利水电出版社，2007.

［2］Rayward-Smith V.J.，Osman I.H.，etc..Midern Henristic search methods［M］.John Wiley ＆Sons Ltd，1996.

［3］Miranda V.，Ranito J.V.，Proenco L.M..Genetic algorithms in optimal distribution network planning［J］.IEEE Trans on Power Systems，1994，9（11）：1927 －1933..

［4］谢敏，敬东.遗传算法在配电网规划中的应用［J］.电站系统工程，2002，18（1）：30 －32.

［5］刘晓飞，彭建春等.基于单亲遗传算法的配电网络规划［J］.电网技术，2002，26（30）：53 －56

［6］韩生廉，周文愚.基于免疫更新机制的遗传算法及其在规划问题中的应用［J］.控制与决策，2002，17（3）：20 －23.

［7］颜伟，王丽娜.基于改进免疫遗传算法的配电网网架规划［J］.重庆大学学报：自然科学版，2007，30（1）：29 －30.

［8］蒙文川，邱家驹.基于免疫算法的配电网重构［J］.中国电机工程学报，2006，8：470 －40.

［9］李靖霞，鞠平.配电网络优化规划的基因算法［J］.电力系统自动化，1999，23（20）：12 －14.

［10］王雷，顾洁.中压配电网优化规划的单亲遗传算法［J］.电力系统自动化，2006，18（3）：72 －76.

［11］焦李成，杜海峰，等.免疫优化计算、学习与识别［M］.北京：科学出版社，2006.

［12］周湶，孙才新，张晓星.基于多种群免疫遗传算法的配电网网架规划［J］.重庆大学学报：自然科学版，2005，28（4）：36 －40.