系统动力学在中学力学问题中的应用

葛 洲

(南京外国语学校,江苏南京 210008)

上世纪60年代,美国福瑞斯特教授提出系统动力学,在其发展过程中取得了很多令人瞩目的成果,许多学者纷纷采用系统动力学方法来研究各自领域的问题,涉及到经济、能源、交通、环境、工业、城市等许多领域.美国较早在K 12教学中应用系统动力学,从小培养学生的系统思考能力,国内从2002年开始了探索系统动力学在中学教学中的应用.在中学物理的研究性学习中应用系统思考,既可以让学生从系统的角度加深对所学物理知识的理解,也可以培养学生系统思考的能力.

应用系统思考研究物理问题,可以按照如下步骤:(1)认识所研究的问题;(2)构建问题的系统模型;(3)STELLA软件模拟(STELLA是系统动力学的模拟软件之一);(4)调试与检测.

系统思考及其模拟软件 STELLA为学生提供了一个很好的研究性学习的平台,学生在学习物理知识的同时,培养了他们的系统思考能力.现举系统动力学在中学物理教学中应用的实例如下.

1 自由落体运动的分析

自由落体运动是指物体只在重力作用下,由静止开始的下落运动,自由落体运动系统中的变量及其关系如图1.

图1

图2

根据变量之间的关系,用STELLA软件建模如图2:

设置变量初始值及变量关系如下:

初始值:

速度 =0;位移=5m;质量=5 kg;力=50 N.

变量间的关系:

速度(t)=速度(t-dt)+(加速度)*dt;

加速度=力/质量;

位移(t)=位移(t-dt)+(速度)*dt.

运行软件得到自由落体运动的速度-时间图像和位移-时间图像如图3.

图3

图3中1线为位移-时间图像,2线为速度-时间图像,速度-时间图像为直线,表明自由落体运动是匀加速直线运动.

2 考虑阻力落体运动的分析

如果考虑物体由静止下落过程中受到空气阻力,引入阻力因数,设空气阻力与速度成正比,则此系统中各个变量及其关系如图4,比较图1和图4,图4在图 1基础上增加了速度对加速度的反馈,此反馈为负反馈,即速度的增加会引起加速度的减小,速度增加变慢.此类问题达到一个稳定的结果.

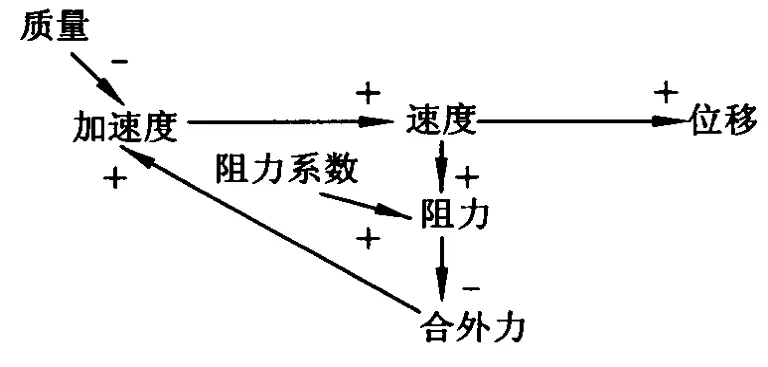
图4

根据变量之间的关系,用STELLA软件建模如图5.

常量,变量初始值和变量间的关系如下:

常量及初始值:

质量=5kg;位移=0;阻力系数=2kg◦s-1;

变量关系:

速度(t)=速度(t-dt)+(加速度)*dt;

位移(t)=位移(t-dt)+(速度)*dt;

图5

加速度=力/质量;合力=50+阻力;阻力=—速度*阻力系数.

运行软件得到有阻力的落体运动的速度-时间图像和位移-时间图像如图6.

图6

图6中1线为速度-时间图像,2线为位移-时间图像,此时速度图像不再是直线,而是趋近于某一定值,位移图像不再是抛物线,变化趋近于线性变化.

图7

3 弹簧振子的分析

在考虑阻力的落体运动中,速度对加速度有负反馈,而在考虑阻力的弹簧振子模型中,如图7,不仅有速度对加速度的负反馈,位移对加速度也有反馈,那么振子的运动情况将怎样呢?

图8

此系统中各个变量及变量间的关系如图8.

根据变量之间的关系,用STELLA软件建模如图9.STELLA软件给出的变量初始值和变量间的关系如下.

常量及变量初始值:

劲度系数=0.5Nm-1;质量=5 kg;阻力系数=0.5 kg◦s-1;速度=0;位移 =5 m;

变量之间关系:

速度(t)=速度(t-dt)+(加速度)*dt;加速度=力/质量;

位移(t)=位移(t-dt)+(v)*dt.

合力=弹簧弹力+阻力;阻力=-速度*阻力系数;弹簧弹力=-劲度系数*位移.

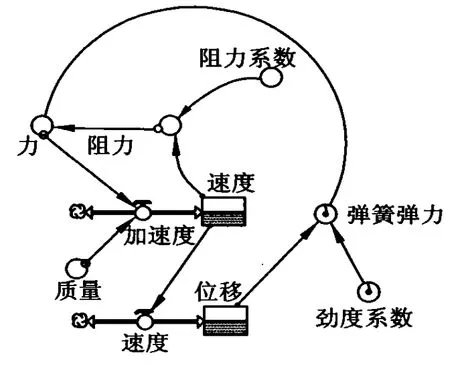
图9

运行软件得到阻尼振动的振子的速度-时间图像和位移-时间图像如图10.

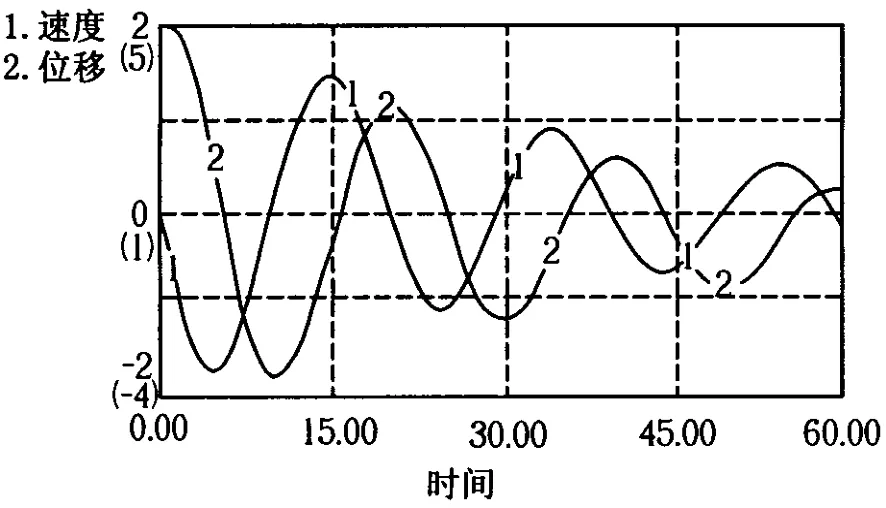
图10

图11

改变阻力系数的大小,运行软件可以模拟过阻尼和临界阻尼的情况.如图11.

自由落体运动是最简单的匀变速直线运动,如果考虑落体运动中的阻力对加速度的负反馈,运动将变成变加速运动,如果只考虑到位移对加速度的反馈,则物体做简谐运动,在简谐运动基础上,再考虑到阻力对加速度的负反馈,物体将做阻尼振动,可通过STELLA软件模拟各种阻尼条件下的位移-时间图像和速度-时间图像.

4 一道高考题的分析

2010年江苏高考题第8题,其实也可看做是位移对加速度反馈的系统动力学问题.

图12

原题.如图12所示,平直木板AB倾斜放置,板上的P点距A端较近,小物块与木板间的动摩擦因数由A到B逐渐减小.先让物块从A由静止开始滑到B,然后,将A着地,抬高B,使木板的倾角与前一过程相同,再让物块从B由静止开始滑到A.上述两个过程比较,下列说法中一定正确的有

(A)物块经过P点的动能,前一过程较大.

(B)物块从顶端滑到P点的过程中因摩擦产生的热量,前一过程较少.

(C)物块滑到底端的速度,前一过程较大.

(D)物块从顶端滑到底端的时间,前一过程较长.

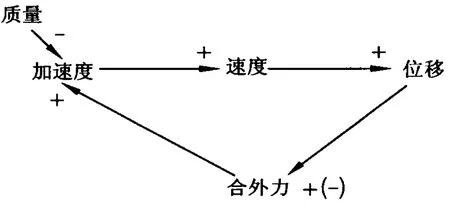
图13

此系统中各个变量之间的关系如图13,由于从A到B动摩擦因数逐渐减小,所以,从A到B运动位移越大,阻力越小,合力越大,加速度越大,位移对加速度有正反馈.而从B到A,位移对加速度有负反馈.

根据变量之间的关系,用STELLA软件建模如图14.

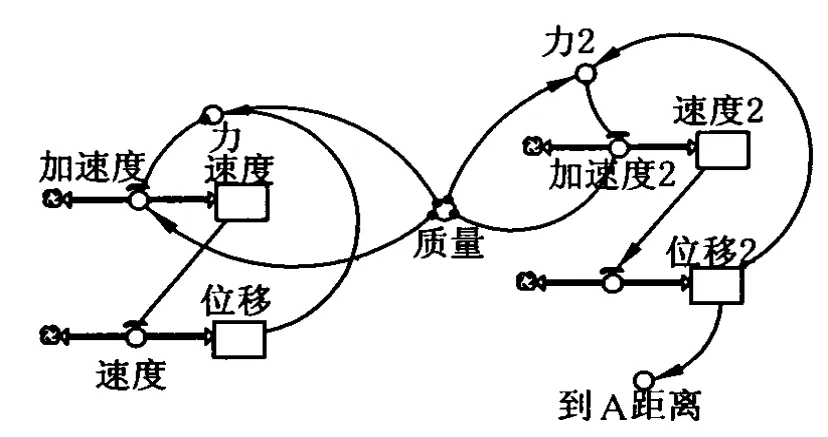
图14

其中速度、加速度、位移、力为下降过程中的物理量,速度2、位移2、速度2、力2为上升过程的物理量.

根据题意,在建模过程中,设木板长度为100 m,摩擦力f=4-0.039x,x为物体离开A点的位移.

常量及变量初始值:

速度=0;速度2=0;位移=0;位移2=0;质量=1 kg.

变量之间关系:

速度(t)=速度(t-dt)+(加速度)*dt;

加速度=力/质量;

速度2(t)=速度2(t-dt)+(加速度2)*dt;

加速度 2=力2/质量;

位移(t)=位移(t-dt)+(速度)*dt;

位移2(t)=位移2(t-dt)+(速度2)*dt;

力=质量*9.8*0.5-(4-位移*0.039);

力2=质量*9.8*0.5-(0.1+位移2*0.039);

离A距离=100-位移2.

运行软件得到如图15图像,其中线1表示从A到B过程的位移-时间图像,线2表示从B到A过程的位移-时间图像.

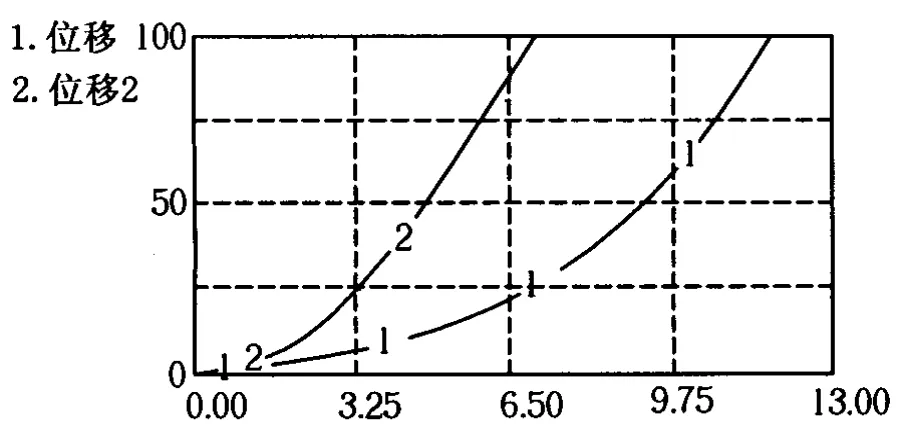
图15

从图15中可以看出,从A到B过程,完成100 m位移所用的时间较长.

运行软件也可得到如图16图像,其中线1表示从A到B过程的位移-时间图像;线2表示从B到A过程的位移-时间图像;线3表示从A到B过程的速度-时间图像;线4表示从B到A过程的速度-时间图像;线5表示从B到A过程中,物体离A点的距离.

根据题意,可设线1与线5的交点为题中提到的P点,在图中过P点作时间轴的垂线,此虚线与线 3、线4的交点分别为C、D.从图上可以看出 vC＜vD,所以,下降过程经过P点的速度比上升过程经过P点的速度小,所以经过P点的动能,前一过程较小.

图16

综上所述,可选出(A)、(D)选项,根据能量守恒或图16,不难看出(B),(C)选项是错误的.