拆基本图证几何题
2011-07-25430300湖北省武汉市黄陂区实验中学
中学数学杂志 2011年24期
430300 湖北省武汉市黄陂区实验中学 程 斌
题目(武汉市2011年九年级四月调考第24题)在等腰△ABC中,AB=AC,分别过点B,C作两腰的平行线,经过点A的直线与两平行线分别交于点D,E,连接DC,BE,DC与AB边相交于点M,BE与AC边相交于点N.
(1)如图1,若DE∥CB,写出图中所有与AM相等的线段,并选取一条给出证明;
(2)如图2,若DE与CB不平行,在(1)中与AM相等的线段中找出一条仍然与AM相等的线段,并给出证明.
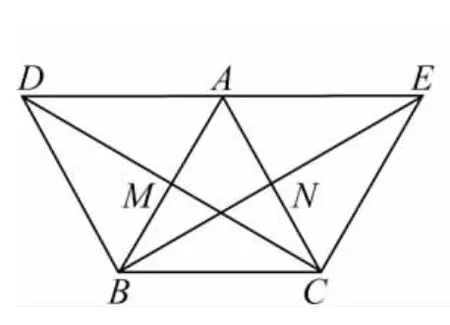
图1
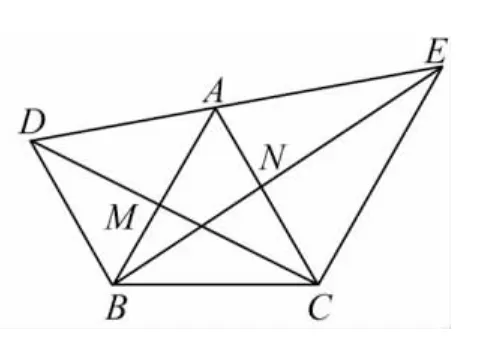
图2
分析第(1)问由平行四边形对角线互相平分可得与AM相等的线段有AN,BM,CN.第(2)问图形由特殊到一般且结论开放.
求解在明确结论AM=CN的前提下就证明方法作如下探讨.
证明(2)法1利用平行线分线段成比例将原题拆成基本图3(①~④)
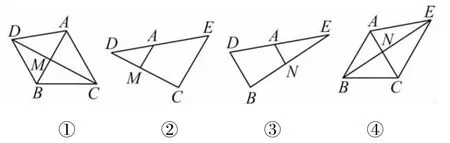
图3
法2利用三角形相似将原图拆成基本图4(⑤~⑦)
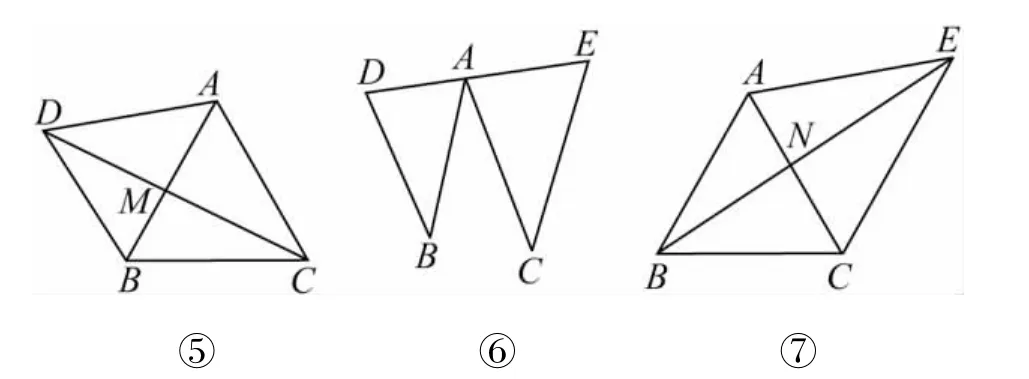
图4
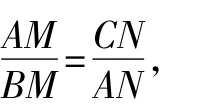
再利用比例性质可得AM=CN.
法3分别延长DB,EC相交于点P,则四边形ABPC为菱形.
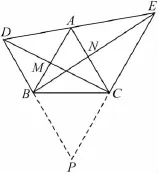
将原题拆成基本图5(⑧~⑩)
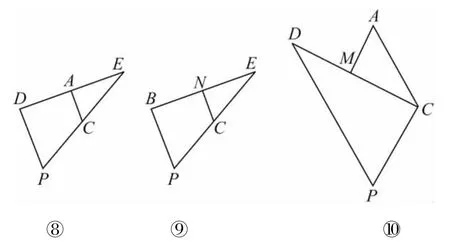
图5
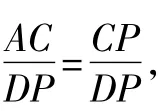
即证得AM=CN.
法4过点E作AC平行线交BC的延长线于点F,则可得CE=EF.
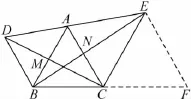
将原图拆成基本图6(○11 ~ ○13)
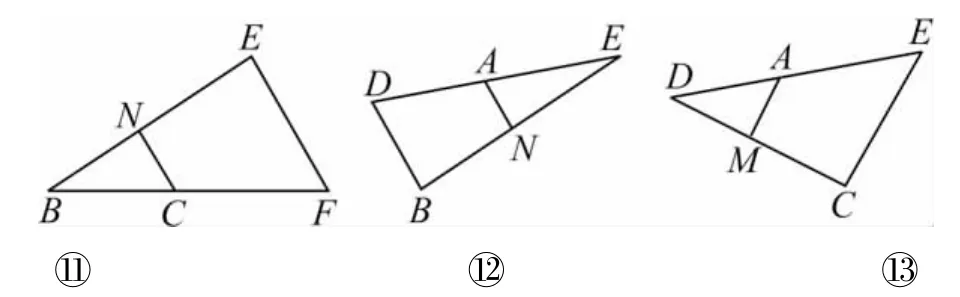
图6
由CE=EF可得AM=CN.
