多跨U形管固有频率的计算

聂清德，谭 蔚，吴 皓

(天津大学 化工学院，天津 300072)

符号说明:

di——U 形管内径，m

do——U 形管外径，m

E——U形管材料的弹性模量，MPa

fn——直管的固有频率，Hz，下标n为振型的阶数

fU——U形管的最低固有频率，Hz

l——折流板间距，m

l1——半圆形的弯管端与相邻折流板间的距离，m

l2——管板与相邻折流板间的距离，m

m——单位管长的质量，kg/m

n——跨数

R——弯管中心线的半径，m

λn——直管的频率常数，无因次

λU——U形管的频率常数，无因次，其值与管子的振型，管子的支承方式，参数 l1/l，l2/l，R/l等有关

ρ——U形管材料密度，kg/m3

0 引言

U形管换热器因能消除管壳间温差应力和具有结构简单、造价便宜、管外易清洗等优点，在化工、炼油、动力和核能工业中都有广泛的应用。但是由于U形弯管的存在，此类换热器管束固有频率较低，极易在横向流中引起振动。因此准确并快捷地计算多跨U形管的固有频率特别是它的最低固有频率，将非常有利于对换热器进行振动分析和安全评估。

U形管固有频率的计算方法可以分为理论计算方法和简化计算方法。前者可以通过联立求解振动方程得出U形管的频率方程，进而求出U形管的固有频率［1－2］。理论计算方法的优点是准确度高，但因计算过于繁复，必须依赖电算，从而在一定程度上限制了其在工程中的应用。后者多是建立在有限元等方法的数值分析的基础上，并通过实验验证得出的半经验公式。诸如莫雷蒂(P.M.Moretti)等提出子系统的计算方法［3－4］，TEMA标准推荐的分跨段的计算方法［5］，笔者在文献［6－8］中提出的全系统的计算方法等均属此范畴。由于简化计算方法使用方便快捷，且有相当高的准确性，所以对此类方法的研究与完善，在工程界受到广泛的重视与期待。

1 简化计算公式

在列管式换热器中，要计算单跨直管的固有频率fn，只需通过应用经典的力学理论求解四阶微分方程而获得计算公式(1)［9－10］，就很容易地求出其精确解。

式中 λn——频率常数，依据振型阶数，管端固定条件确定

如图1所示的多跨U形管，要计算其固有频率或最低固有频率fU，情况便复杂很多。必须联立求解14个基本方程式才能得到精确解［1－2］。通常均借助电算来完成。随着有限元法的推广应用，以及日益成熟的商用有限元程序的问世，使准确地进行数值计算与分析成为可能。在此基础上可仿照式(1)的形式提出计算多跨U形管最低固有频率的简化公式，即:

只要确定频率常数 λU，fU的计算便迎刃而解。

图1 多跨U形管示意

2 U形管频率常数图

莫雷蒂等提出的子系统计算方法与TEMA法是一致的。它将U形管划分为多个子系统(见图1)，计算出各个子系统的固有频率，取其中的最小值作为U形管全系统的固有频率。一般情况下，3跨简支子系统的固有频率是最低的且可按公式(2)进行计算［3－4］。莫雷蒂等还发现3跨简支子系统与7跨简支子系统的固有频率非常接近，因此认为按照3跨简支子系统的参数作出的频率常数图具有通用性。

笔者在文献［6－8］中则提出直接按U形管全系统的支承条件来确定其固有频率以简化计算步骤。还通过计算得知，在其他参数相同的情况下，7跨U形管与13跨U形管的固有频率基本上是一致的，因此建议在应用式(2)或(3)时，可根据按7跨U形管的参数作出的频率常数图确定λU值。

在本文中，笔者又进一步利用ANSYS有限元程序，对影响U形管的固有频率或频率常数的参数进行了更为全面的分析。分析时取U形管的支承形式为对称支承与非对称支承，影响参数范围为:n=3 ～ 21，l1/l=0.0 ～1.0，R/l=0.0 ～1.0，l2/l=1～2。在此基础上提出了改进的频率常数图，以提高计算的准确度。

3 频率常数影响参数的分析

3.1 端部固定条件的影响

图1示出工业中常用的多跨U形管的示意图。管子的支承条件是:在管板端为固支，在折流板处为简支。端部固定条件对频率常数的影响可通过图2反映出来。

当跨数为3时，端部简支U形管的频率常数曲线明显地位于端部固支U形管的频率常数曲线之下。对称支承的 U形管在 l1/l≤0.4，R/l＜0.3，差别很大;而非对称支承时在整个参数范围内，差别都较大。

当跨数增大后，端部固定条件对频率常数的影响减弱。端部简支3跨U形管的频率常数曲线与端部固支7跨U形管频率常数曲线之间的偏离程度减小。但在非对称支承条件下，R/l较小时，偏离程度依然较大。

3.2 跨数对频率常数的影响

利用图2也可以对端部均为固支、跨数分别为3，7的U形管频率常数曲线作一比较。可以看到，在大部分范围内两组曲线比较接近，但在R/l较小时呈现出较大的偏差。

图3(a)与3(c)示出了在对称支承条件下，端部固支，l1/l=0 ～1.0，R/l=0 ～1.0，l2/l=1.0，跨数分别为5，7，13，17，21的 U 形管频率常数曲线的比较。在绝大部分范围内各组曲线基本上是重叠的。若以7跨U形管的频率常数为基准计算其他U形管频率常数的误差(见表1)，总体误差都小于1%，最大误差8.19%，但却是出现在实际上极少遇到的R/l=0处。可知在所定的参数范围内，跨数对频率常数的影响可以忽略不计。

图2 频率常数比较图

图3(b)与3(d)示出了在非对称支承条件下，端部固支，l1/l=0 ～1.0，R/l=0 ～1.0，l2/l=1.0，跨数分别为 4，5，7，13，17，21 的 U 形管频率常数曲线的比较。由于结构的非对称性，跨数增大后，频率常数曲线下移，频率常数稍有减小。如仍以7跨U形管的频率常数为基准来计算其他U形管频率常数，总体误差增加不多，但在R/l=0.015～0.18的局部范围内，最大误差高达24.57%(见表2)。如果在跨数为13～21范围内改以17跨U形管的频率常数为基准进行比较，由表3可知，总体误差与最大误差都显著地降低。

从以上分析可知，当应用简化方法计算U形管的固有频率时，应根据跨数的不同选用相应的误差较小的频率常数图。

3.3 端跨长度的影响

图3 频率常数比较图

表1 对称支承时以7跨U形管频率常数为基准计算的误差

在工业换热器中，位于壳程进出口处的直管段l2可能比较长，因此在计算时还需考虑到端跨长度对频率常数的影响。

表4列出当端跨长度和参数l1/l，R/l改变后，对称支承的7跨U形管固有频率变化的数据。

由表4经分析可知，随着l2/l的变化，U形管的振动变形可分为3种类型:

表2 非对称支承时以7跨U形管频率常数为基准计算的误差

(1)当l2/l较小，l1/l或R/l相对较大时，l2/l增大后，U形管的固有频率变化不大。振动时主要是弯管段的面外振动变形(见图4)。

(2)U形管的固有频率随l2/l增大而开始减小，但减小的幅度不大，振动时主要是系统整体变形(见图5)。

(3)U形管的固有频率随l2/l增大迅速减小，固有频率变化同多跨直管的变化接近，振动时主要是端跨直管段的振动变形(见图6)。

此外，当l1/l和R/l较小时U形管固有频率随端跨长度的变化和多跨直管的相同，其振动变形如图7所示。

表3 非对称支承时以17跨U形管频率常数为基准计算的误差

3.4 本文计算方法

综上所述，文中仍推荐利用式(2)或(3)计算多跨U形管的最低固有频率。但应根据支承方式、跨数、端跨长度的不同，按照图8，9中相应的曲线来确定频率常数。

表4 对称支承时l2改变后7跨U形管的固有频率 Hz

图4 弯管段为主的振动变形

图5 整体振动变形

4 各种计算方法对比

文中推荐的方法与子系统方法以及TEMA方法的计算数据比较如表5所示。可知利用本文推荐方法的计算结果与ANSYS程序的计算结果完全一致，与实验值比较［8］，误差在 0.38% ～13%之间，结果令人满意。

也可看出，不管是子系统还是TEMA标准的计算方法，都是比较保守的，而且前者提供的频率常数曲线不完整，后者提供的数据较为狭窄，使用都受到一定限制。

图6 端跨直管段为主的振动变形

图7 l1/l和R/l较小时多跨管的振动变形

图8 对称支承时U形管频率常数图

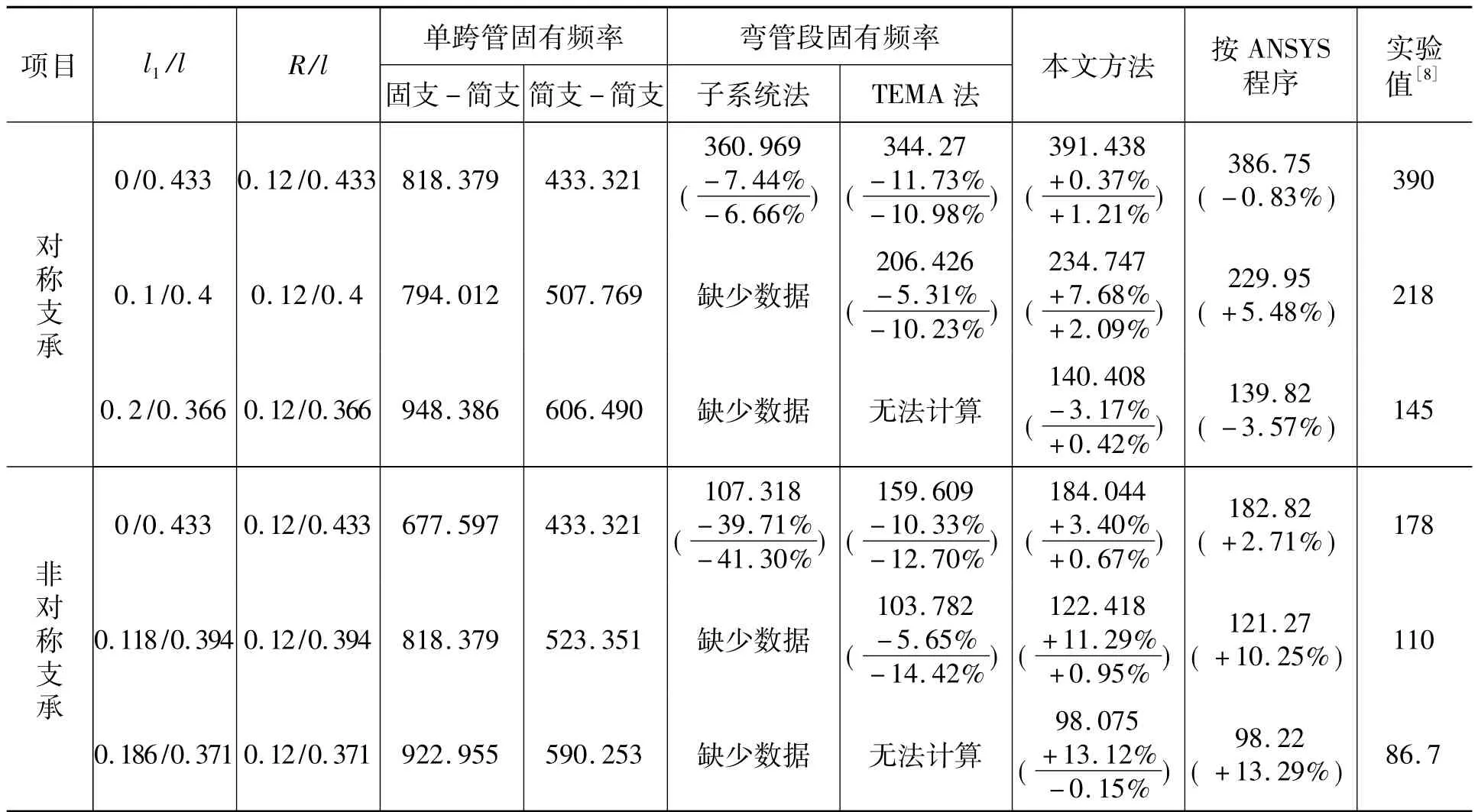
表5 U形管的固有频率fU Hz

图9 非对称支承时U形管频率常数图

5 结论

通过采用有限元数值计算方法对不同参数条件下的U形管系统的固有频率所作的较为全面的计算与分析，得出了以下结论:

(1)采用端部固支多跨U形管全系统为依据的计算方法比采用3跨简支子系统为依据的计算方法更为简捷且能得到更为准确的计算结果。

(2)在对称支承条件下，仅在跨数为3且弯管半径较小时跨数对固有频率影响较大。当跨数大于3，跨数对固有频率的影响可以忽略不计。采用端部固支7跨U形管的基本参数为依据作出的图8(b)适用于在较大跨数范围内进行近似计算。

(3)在非对称支承条件下，考虑到跨数对固有频率有一定影响。在对误差分析的基础上，可利用图9(a)～9(c)分别计算不同跨数条件下的U形管系统的固有频率。

(4)端跨长度增大后，U形管的固有频率将会降低，或仍维持不变，这与参数R/l与l1/l的数值密切相关。变化的大小在图8(b)，图9(b)，图9(c)中明显地反映出来。此外，当参数R/l和l1/l较小或端跨长度较大的情况下，U形管系统可近似地看作是多跨直管系统，可按直管系统进行计算，相应的参数范围可利用U形管的频率常数图和多跨直管的频率常数来确定。

［1］Gorman D J.Exact Analytical Solutions for the Free Vibration of Steam Generator U － tube［J］.Journal of Pressure Vessel Technology，1988，110:422 －429.

［2］Singh K P，Soler A I.Mechanical Design of Heat Exchangers and Pressure Vessel Components［M］.Arcturus Publishers，Cherry Hill，N.J.，1984.

［3］Moretti P M.Fundamental Frequencies of U－Tubes in Tube Bundles［J］.ASME，Journal of Pressure Vessel Technology，1985，103:207 －210.

［4］Nguyen D C，Lester T，Good J K，et al.Lowest Natural Frequencies of Multiply Supported U － Tubes［J］.ASME，Journal of Pressure Vessel Technology，1984，106:414－417.

［5］Standards of Tubular Exchanger Manufactures Association［S］.9th Ed，2007.

［6］聂清德，张明贤.U形管的自振频率［J］.石油化工设备，1990，19(4):5 －9.

［7］Nieh(Nie Qingde)C D，Zhang M X.Natural Frequencies of Exchanger U － Tubes［J］.Hydrocarbon Processing，May，1991:97 －100.

［8］聂清德，金楠，聂勇，等.U形管固有频率的计算［J］.化工设备设计，1995，(6):8 －14.

［9］铁木辛柯.工程中的振动问题［M］.北京:人民铁道出版社.1978:281－289.

［10］聂清德.化工设备设计［M］.北京:化学工业出版社.1991:115－118.