基于共同模式挖掘的时间序列相似性度量方法
2011-07-24贾湖,朱博
贾 湖,朱 博
(天津大学 管理与经济学部,天津 300072)
0 前言
时间序列相似性度量在数据挖掘领域有着广泛的应用,如频繁模式聚类,关联规则挖掘等。时间序列的相似性度量包括两个子序列的相似性度量和整个序列的相似性度量。对相似性这一概念的定义取决于实际问题中所要处理的时间序列的特点和数据挖掘的目的,例如对于每日的股票收盘价这一时间序列数据,两只股票的价格可能相差数倍,但却有着大致相同的走势。对投资者而言,这样的股票应该是相似性比较高的,而不是股价接近,走势却完全相反的股票。因此,在进行相似性研究时,要针对不同的数据和挖掘目标,使用不同的相似性度量方法。影响序列相似性的因素主要有:噪声,水平移动,振幅伸缩,线性偏移,不连续性等。本文将以股票价格数据为基础,对各种时间序列的相似性度量方法进行比较,并针对整个时间序列的相似性问题提出一种新的基于共同模式挖掘的度量方法。
1 时间序列相似性度量方法
1.1 直接距离法
通过计算两个序列之间的距离来衡量两序列的相似性是一种很容易理解的方法,距离越大则说明两序列相似性越小,反之则越大,文献[1]对这种方法有详细的介绍。这种方法首先应该解决的问题便是如何定义两序列的距离,有三种函数可用于描述两序列的距离:曼哈坦距离、名可夫斯基距离、欧式距离。其中最常用的是欧式距离,欧式距离的定义为:

x和y分别代表两个时间序列,xi和yi分别是x和y中的第i个点。欧式距离是一种简单且直观的距离测定方法,其计算复杂度与时间序列的复杂度成线性关系。对于股票价格这样长度较大的时间序列来说其欧式距离会是一个很大的值,而且两只股票价格的相对高低会对其影响很大,因此不适于做股票价格时间序列的相似性度量。
1.2 傅立叶变换法[2]
傅立叶变换的基本思想是将时间信号分解成一系列不同频率的正弦波的叠加,其实质是将序列从时间域转到频率域,然后再进行处理。对于有限序列,傅立叶正变换为:

经过傅立叶变换的信号能够保持原来的能量不变,而且在频域空间中,序列的能量通常集中在几个主要频率上。可以将能量较低的频率过滤掉,滤波后的序列和原序列仍然是很相似的,即傅立叶变换能够有效的将序列进行压缩。采用傅立叶变换后的欧式距离度量相似性,其拒识率一般比时域空间中的欧式距离法低。在这里,拒识率指的是原本很相似的序列计算出的相似性度量值却很低的概率。利用傅立叶变换处理后的数据再用欧式距离进行相似性度量能大大降低需要计算的数据量。
(3)动态时间扭曲法
动态时间扭曲法(DTW)是Berndt和Clifford[3]引入时间序列研究中的,该方法首先用长度为m和n的两个序列构造一个m×n的距离相异矩阵D。然后寻找一条由矩阵中满足一定条件中路径,使其连接矩阵的始末两点。该模型可以度量长度不同的序列,同时对于噪声、振幅变化等具有一定的鲁棒性,但是该方法的计算量相当大,尤其不利于长度较大的序列的相似性度量。文献[4]提出ASEAL和SEA方法在处理复杂时间序列和提高算法效率方面比DTW法更加优越。
(4)基于规范变换的方法
Agrawal[5]等认为如果两个序列有足够多的、不相互重叠、按时间顺序排列且相似的子序列,则这两个子序列相似。其基本思想是采用宽度为w的滑动窗口将序列分成若干个原子序列,对每个原子序列W=(w1,w2,…,wn),先按照如下的方法进行偏移变化和幅度缩放:

其中wi是窗口序列W中的第i个元素,wmax和wmin分别是窗口中最大和最小元素,为变化后序列元素。对两个原子序列 W1=(w11,w12,w1n)和 W2=(w21,w22,w2n),若所有的序列元素满足:

则称两子序列相似,当两个序列的相似子序列达到一定数量时,可以判定两序列相似,并用相似子序列的对数与窗口数的比值作为相似性的度量值。该方法考虑了幅度伸缩、偏移等问题,但是窗口大小和限定参数的设置仍然是困难的。本文不再将序列按照固定的窗口进行分割,而是采用大小可变的窗口,这样就能避免将不再同一趋势模式内的点硬性分到同一窗口所造成的误差。
除此以外,还有神经网络法[6],基于离散小波变换[7],相关性测度法[1],界标模型法[8]等度量方法。
2 算法概述
在对时间序列进行关联规则挖掘和模式聚类时,需要将整个时间序列分成若干子序列,然后对具有相同特性的子序列进行频繁模式挖掘,发现具有共同特点的频繁子序列集。本文在总结前人对时间序列相似性研究的基础上,提出了一种新的基于共同模式挖掘的相似性度量方法。序列分割一般采用的方法是等长分割,这种方法最大的好处是分割后的各个子序列是同步的,但子序列的长度的确定是一个难题,而且强制分割必然破坏潜在模式的完整性,损失大量信息。鉴于此,本文采用了不等长的分割方法。股票价格数据是一种特殊的时间序列,投资者更关心某一个模式的涨跌幅度和持续时间。所以在对序列进行分割时,我们针对每个子序列进行线性回归,当子序列的回归判定系数大于某个给定的阈值r时,将下一个点加入子序列中继续计算;反之,将该子序列保留,从下一个点开始搜寻下一个子序列,直至整个序列搜索完毕。
回归判定系数计算公式:

其中为回归估计值为平均值。在对两个序列进行分割之后,原序列变成了包含若干个子序列的集合,比较两个集合中的各个子序列相似性,如果两个子序列的相似度sim超过给定的阈值时,记两子序列相似。计算相似子序列的对数,除以两个序列子序列数中的较大者,所得结果即为两序列的相似度S。该算法的Matlab实现流程简介如下:
算法名:find_similarity
功能:发现两序列的相似度S。
输入:两序列A,B,时滞阈值ΔT,子序列相似性阈值θ,子序列个数差异阈值ε,子序列回归判定系数r;
输出:两序列相似度S:
第一步:将两序列A和B分割成子序列集series_A和series_B(回归判定系数阈值r);
第二步:判断series_A和series_B中元素个数的差值是否小于阈值ε。若小于,则继续,否则,两序列无法匹配,结束程序;
第三步:计算子序列集中相似子序列对的个数count

第四步:计算两序列的相似度S=count/max(|series_A|,|series_B|)。
算法结束。
其中,子序列的相似度sim的计算方法为:设两子序列分别为两个向量a和b,其序列的斜率和长度分别用向量的方向和模长来表示,子序列的相似度即两向量的相似度为:
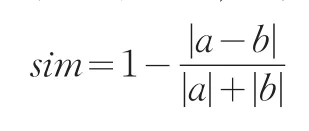
3 算法中的参数
该算法需要提供的参数为:时滞阈值ΔT,子序列相似性阈值θ,子序列个数差异阈值ε,子序列回归判定系数r。其中很明显子序列个数差异阈值ε对于进行相似性度量的时间序列具有筛选作用,考虑到大多数提供用于比较的序列长度应相差不大,因此该变量对算法准确性的影响并不大。下面主要讨论一下ΔT、θ和r对相似性度量的影响。
从上证交易所上市的化工行业股票中选择两只股票sh600110和sh600281,截取其从2009-4-13到2010-7-9日共300天的股票收盘价数据进行序列相似性度量。首先对两组时间序列数据进行预处理,将由于停盘导致的两组数据时间不一致的点通过添加或删除对齐。然后得到两组共600个对称的数据,进行相似性比较,默认参数值为:ΔT=5,θ=0.9,r=0.8,
计算过程在Matlab中编程实现。通过改变参数的值,测定不同参数值下的相似度S,得到参数ΔT、θ和对相似度S的影响。最后结果在图1,图2和图3中表示。

图1

图2

图3
从图1我们可以看出,相似度随着ΔT的增长而增长,同时在ΔT<4时,S增长较快,超过0.5之后则增长明显放缓。图2中θ在0.6之前没有变化,保持一个很高的相似度值,这是因为子序列相似性阈值比较小时,对其起不到筛选作用,而太大(超过0.9)又会变得十分苛刻,使得相似度急剧下降。图3表明当相关性判定系数r小于0.6时,相似性的度量值显示出很差的稳定性,当r超过0.6之后,相似性有一个连续上升的过程。但r不应过大,否则会导致只有很少的点能被加入到子序列中,最终会造成序列被过度分割。综上所述,以上三个参数应在一下范围内应用:ΔT~[3,5],θ~[0.7,0.9],r~[0.7,0.9]。当然,这样给出的范围带有一定的主观性,在具体应用时可以根据个人偏好进行适当调整。
4 时间序列相似性影响因素

图4
在对算法中各个参数进行考量之后,我们得出了3个参数的可用值的范围,现在取 ΔT=5,θ =0.9,r=0.8,对影响时间序列形似性的各个因素进行敏感性研究。
4.1 噪音(NOISE)
设Y为观测值,y为真实值,a代表噪音震荡幅度,σ为随机变量,范围是[0,1]。噪音的影响可用公式表示为:
Y(t)=y(t)+a∗σ(t)
以上文提到的sh600281的数据为原始序列,对原始序列y(t)加入噪音,使其变为Y(t)。通过改变加入噪音的震荡幅度a(从0到10),计算出不同大小的噪音对序列Y(t)和y(t)的相似度S的影响。很明显,当a=0时,S=1,结果如图4所示:当噪声幅度较小时,对相似度S的影响很大,随着噪声的增加急剧降低;当a大于4时,S变化变得缓慢,基本维持在一个较低的值附近上下波动,此时两序列几乎没有相似性。
4.2 水平移动(HORIZONTAL MOVE)
两序列在水平方向的相对移动是另外一个重要的因素,它可以用以下的公式来表示:
Y(t)=y(t+b),其中b为水平移动步数,它代表某个模式和它相似的模式之间可能有几天的超前或滞后。取b从1到10,计算出的相似度S变化如图5所示,可以看出在b=5时S有较大幅度的降低,这一点和我们所设定的ΔT=5的默认值有关系。当b<5时,b的变化对相似性几乎没有影响,因为这一影响可以被ΔT=5的判定阈值所覆盖;当b≥5时,b的变化引起了相似度的大幅波动,但是S仍维持在0.7以上,说明b对S的影响并不是很大。
4.3 振 幅(AM⁃PLITUDE)
定义振幅A>0,对于相似模式而言,振幅改变了子序列的斜率,但并不影响子序列的水平距离和长度,其公式为:
Y(t)=A∗y(t)

图5
如图6所示:振幅在1附近时对相似度S没有影响,S保持为1。随着A增加,S逐渐减小至一个较低值,可见,当A大于2时,A是影响S的一个很重要的因素。
此外,还有一些因素如:序列不连续性,线性偏移,水平伸缩等会对序列相似性起到一定的影响,篇幅所限,本文不再一一赘述。可以推断,对于股票数据来说,噪音、振幅应该是影响相似性的重要因素。因为面对同样的宏观环境的影响,不同行业,不同地域,不同规模的公司所受的影响是有差异的,这也就解释振幅的增加所造成的股票序列相似性的降低。对于不同的公司处理突发事件的能力不同,同时市场的震荡和众多投资者所产生的羊群效应也会干扰个别股票的表现,这些又造成了影响股票序列的噪音。不同序列的同一模式所受到的作用力的释放需要一定的时间,但这并不影响共同模式的发生,因此可以解释序列相似性对于水平位移的不敏感性。
5 应用
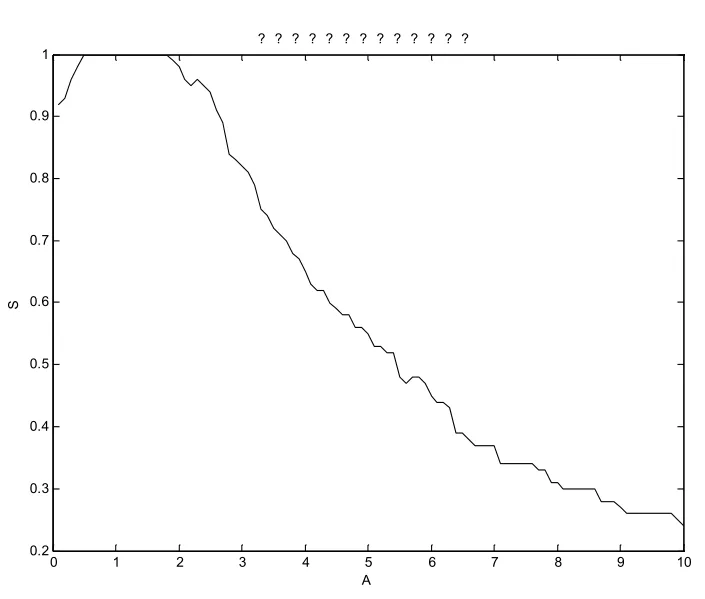
图6
如前所述,在对时间序列进行数据挖掘过程中,序列相似性对于寻找频繁模式,发掘关联规则有着重要的意义,这是时间序列相似性度量的主要应用领域。股票价格数据是一种典型的时间序列数据,受随机因素的影响很大,而且不同行业的股票价格受同一因素的影响可能是截然相反的。即使是同一行业内的股票,受同一作用机制的影响所做出的反应也不相同。本文提出的相似性度量方法在序列分割时充分考虑了子模式的发展趋势和模式发生的时滞性,因此能够很好的体现在同一因素作用下两只股票序列的表现,从而进一步可以为投资者合理分配资金,建立可靠的投资组合,分散风险提供依据。以上文提到的sh600110的数据为例,寻找同一行业中与其相似的股票进行相似性度量,发现有较好的区分度,获得最大相似度的股票为sh600281(S=0.85),最小的相似度为sh600319(S=0.53)。
6 总结
在对时间序列(以股票市场数据为研究对象)相似性研究中,提出了一种新的度量股票市场序列相似性的方法。该方法基于对时间序列的共同模式的挖掘,找出两个序列的相似子模式或称子序列,通过共同模式发生的频繁度来度量整个序列的相似性。根据这种思想,本文作者利用Matlab完成的算法的实现过程,并对算法中相应的参数的设置进行了考量。通过对某支股票的数据所组成的时间序列加入干扰因素:噪音,水平移动,振幅等,得出该方法对于时间序列中的噪音和振幅变化有较强的敏感度,但对于时间序列的水平移动或者子序列的时滞差异表现地较为宽容。
[1] 王晓晔.时间序列数据挖掘中相似性和趋势预测的研究[D].天津大学,2004.
[2] 马超群,兰秋军,陈为民等.金融数据挖掘[M].北京:科学出版社,2007.
[3] Berndt D,Clifford J.Using Dynamic Time Warping to Find Patterns in Time Series[A].In:AAA-94 Workshop on Knowledge Discovery in Databases,KDD-94[C].Seattle,Washington,359~370.
[4] Bachir Boucheham.Reduced Data Similarity-based Matching for Time SeriesPatternsAlignment[J].PatternRecognitionLetters,2010 ,31(7).
[5] Agrawal R,Lin K I,Sawhney H S,et al.Fast Similarity Search in the Presence of Noise,Scaling,and Translation in Time Series Database[A].In:Proceedings 1995 Int’l Conference on very Large Database(VLDB’95)[C].1995.
[6] 史中植.知识发现[M].北京:清华大学出版社,2002.
[7] P.K.Dasha,Maya Nayaka,M.R.Senapatia,I.W.C.Leeb.Mining for Similarities in Time Series Data Using Wavelet-based Feature Vectors and Neural Networks[J].Engineering Applications of Artificial Intelligence,2007,20(2).
[8] Peng C,Wang H,Zhang S R,et al.Landmarks:A New Model for Similarity-based Pattern Querying in Time Series Databases[A].In:Processing of the 16th IEEE Int’l Conference on Data Engineering[C].2000.
