随机系数SETAR模型的应用
2011-07-24莫达隆宋立新
莫达隆,宋立新
(1.贺州学院,广西 贺州542800;2.大连理工大学,辽宁大连 116024)
0 引言
门限自回归模型TAR是Tong.H于1978年提出来的,此后Tong和Lim(1980年)又给出了自激发门限自回归模型SETAR。由于SETAR模型能根据自变量的变化,选择不同的线性模型,这种选择转换被称之为机制转换。正是这种机制转换特征恰好描述了现实生活的大量现象,如经济、金融、气候等领域的现象,这些领域的数据受多种因素影响,观测值序列呈现跳跃性的变化,使得SETAR模型在这些领域的数据分析中得到广泛应用。
正如SETAR模型应用者的研究发现,SETAR模型是利用门限空间来改进线性逼近,现实生活的各种系统却充满着时变性,要提高预测的准确性,预测系统模型的回归系数也应该时常得到更新。本文提出随机系数SETAR模型及其应用,并假设其回归系数是一个随机时间变化的随机系数,给出了回归系数的估计方法.实证研究证明,所建立的模型能更准确地拟合现实数据序列,为拓展SETAR模型的应用提供了一种新的方法。
1 随机系数SETAR模型
设
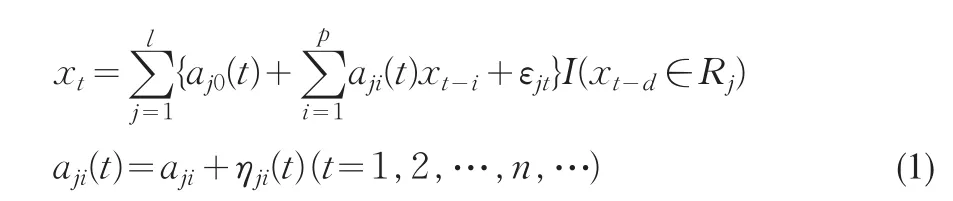
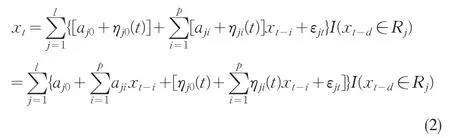

把(3)式写成向量形式:

其中,Y是观测值xt,t=p+1,p+2,…,n,

1.1 模型识别和估计
设xt,t=1,…,n是依时间顺序排列的n个观测值,现要估计参数A,d,确定阶数p和分割{ }Rj.具体步骤如下:
步骤一,假设阶数p和分割{ }Rj已知.根据观测值xt,t=1,…,n给出A的条件最小二乘估计(CLSE),即极小化如下的残差平方和:
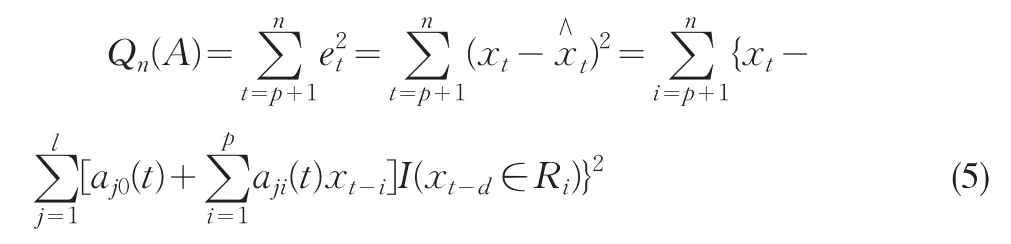
记A的CLSE值为,则

但由(3)式可知,模型(4)是一个异方差模型,宜用加权最小二乘法对模型(4)的系数A进行估计,加权最小二乘估计为
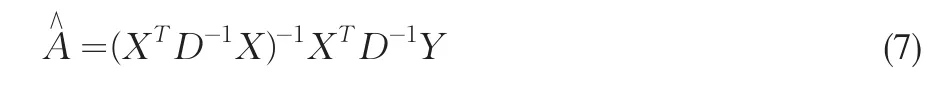
其中,D=diag(dp+1,dp+2,…,dn)是权矩阵

具体计算权矩阵D时,可用模型(4)的CLSE估计的残差估计量作为对角线元素来构造权矩阵D的初步估计。dt是随时间变化的,经过权矩阵D的作用有可能尚未把异方差的因素去掉,可重复地对模型(4)进行加权最小二乘法估计,迭代到模型的残差平方和稳定为止。
步骤二,估计Ri.固定d,关于R极小化,可先根据数据序列直观分析,预先确定一些门限候选值,在这些值处比较最优残差平方和Qn(A)的大小,取使得Qn(A)最小的候选值作为。例如,先将数据序列从小到大重新排列,以位于数据量0.25,0.35,0.45,0.55,0.65和0.75分位数处的xt的取值作为门限候选值。
步骤三,关于d极小化,估计d.对每个固定d,先对j=1,2,…,l,极小化(4)式,然后选择使得(5)式达到最小。

1.2 随机系数SETAR的统计检验
随机系数SETAR的统计检验包括三个方面:
(1)残差的常规检验.如残差的独立性、正态性和等方差性检验。
(2)非线性检验。这里应用广义似然比检验方法,该方法假设检验问题是:
H0:a1i=a2i=…=ali,i=0,1,2,...,p
H1:a1i,a2i,…ali,.i=0,1,2,…,p不全相等。
构造其统计量为:

2 实例分析
2.1 数据获取和初步分析
取广西外经贸2005年1月-2010年4月的出口数据为例分析之(见表1,数据来源:广西商务之窗http://guangxi.mofcom.gov.cn/.统计数据中的进出口数据,单位:万美元)。其中,取2005年1月~2009年12月的出口数据作为分析数据,2010年1月~4月为预测用的数据。(所用统计软件为eviws和R语言,自行编程)
为初步观察数据的平稳性,作广西累计出口月金额数据序列图和相关函数图。由此可以判断:广西累计出口月金额数据序列有明显长期趋势,因是月度数据,很有可能存在季节趋势。可计算其季节指数,若存在季节趋势可先剔除季节趋势,再通过单位根(ADF)检验其平稳性,并确定长期趋势是确定性趋势还是随机性趋势,从而选择适当方法剔除长期趋势即可得到一平稳序列。
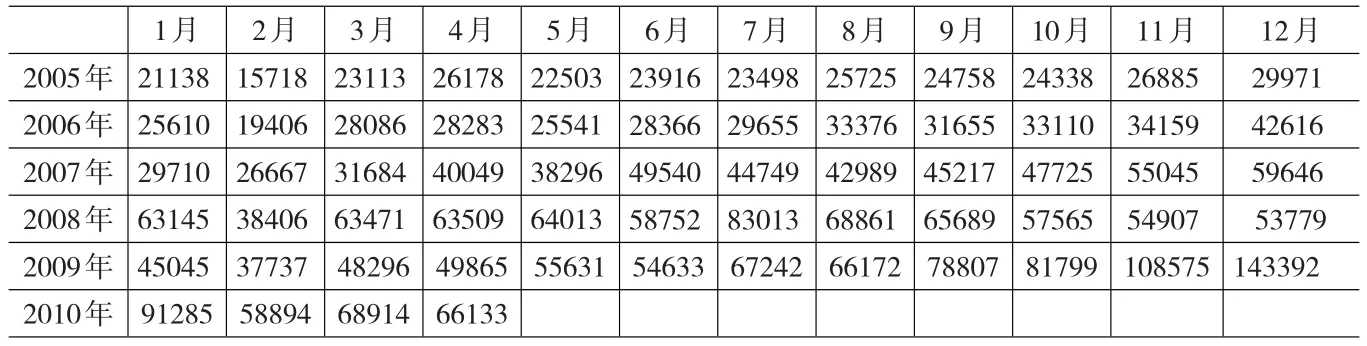
表1
剔除季节趋势的方法有季节差分、计算季节指数再消除季节因素等方法,因为该原始序列的容量较少(n=64),如果用季节差分消除季节因素,势必会缺失相当多的数据。所以通过计算季节指数消除季节因素的方法剔除季节变动。用移动平均法,得广西累计出口月金额数据的季节指数表(见表2):
根据季节指数发现,原序列有季节趋势,在上半年和下半年稍有变化.可剔除季节趋势,设剔除原序列中的季节因素后的序列为{Zt}。
2.2 对序列{Zt}进行ADF检验,确定序列均势类型
经尝试,有如下结果:(见图1,见图2)
图1、图2显示:检验t统计量值是-0.491272,大于显著水平为5%和10%的临界值,同时时间项T的t统计量小于临界值,可断定序列{Zt}存在单位根,是具有随机性趋势的时间序列,对其零均值化,得到的新序列设为{Yt}。因序列{Yt}是具有随机性趋势的时间序列,要通过差分的方法来消除随机性趋势。

表2

图1

图2
经尝试,对{Yt}两阶差分(仍设为序列{Yt})后进行ADF检验,检验t统计量值是-8.906645,小于显著水平为5%和10%的临界值,时间项T的t统计量也小于临界值,表明序列{Yt}是平稳的,滞后项m=2,可初步估计序列{Yt}有滞后项为3的自回归模型。
2.3 利用ARMA(q,p)模型建模
利用Pandit-Wu建模方法对序列{Yt}拟合AR(1)、ARMA(3,1)、ARMA(5,3)、ARMA(4,3)、ARMA(2,1)等模型进行对比选择。
拟合相关结果如下(见表3):

表3
综合表3的各项因素,ARMA(5,4)是一个最佳的模型,模型形式如下:
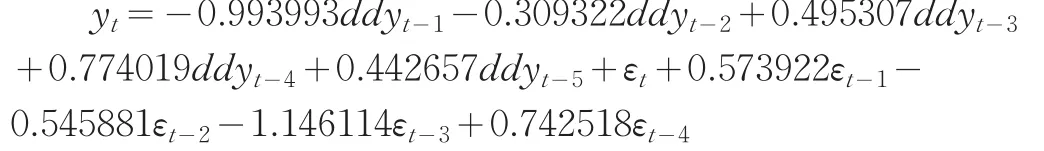
2.4 利用随机系数SETAR模型建模
根据上文的单位根检验可初步确定阶数为p=3,序列有季节趋势且在上半年和下半年稍有变化,可暂取第18个序列数据Y18=-78作为门限值r,d=2(1≤d≤p),由式(6)得到系数A的初步估计

现要进行异方差检验,作模型的残差图和标准残差图,从这两个残差图可明显看出残差呈异方差分布,可利用加权最小二乘法估计模型(4)的系数A。先抽取模型(4)的残差估计量,定义权矩阵D为再由式(6)得系数A的加权最小二乘估计D-1Y。经迭代,A最佳的结果是:

先固定d=2,因数据序列是月度数据,且根据3.1节分析发现数据有两个季度的季节趋势,便取第18、24、36、42个数据作为门限候选值,分别极小化(5)式,发现当r=2872时,式(5)最小,故暂取r=2872.固定r=2872,分别对d=1、2、3时极小化式(5),发现当d=2时,式(5)最小,故取d=2。上述过程用表4来表示:

表4
从表4中可看出,r=2872,d=2时残差平方和最小。因此可建立如下模型
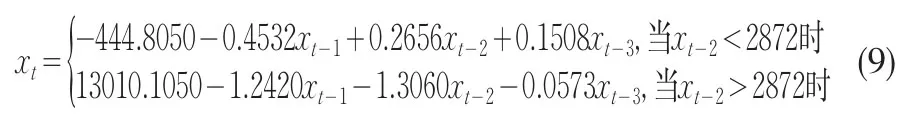
2.5 对模型(9)的统计检验
首先,做残差的常规检验.模型解决了异方差问题,现对残差的独立性和正态性进行检验,结果有:W=0.9776,P-Value=0.4043。满足正态性检验。
然后,进行非线性检验.采用广义似然比检验,有如下结果:
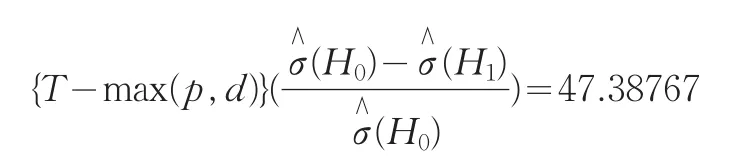
该值远远大于水平0.1%的临界值27.20[4],拒绝H0假设,即线性模型的假设不成立.
最后,对系数进行显著性检验。
R语言编程计算结果如下:


上述结果表明,除了当r>2872时,xt-3的系数不显著外,其他系数的P值均小于0.05,所以应该是非常显著的。相关系数的平方为0.9651,关于F分布的P值也大大小于0.05,也非常显著。因此可以认为模型通过了检验。
2.6 预测
用ARMA(5,4)模型和随机系数SETAR模型预测2010年第一季度的广西出口金额数据的对比,如下表:
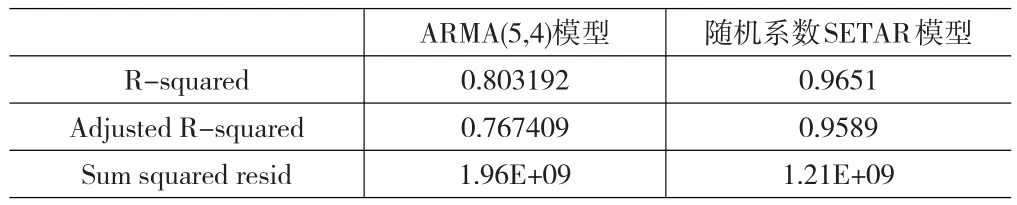
表6
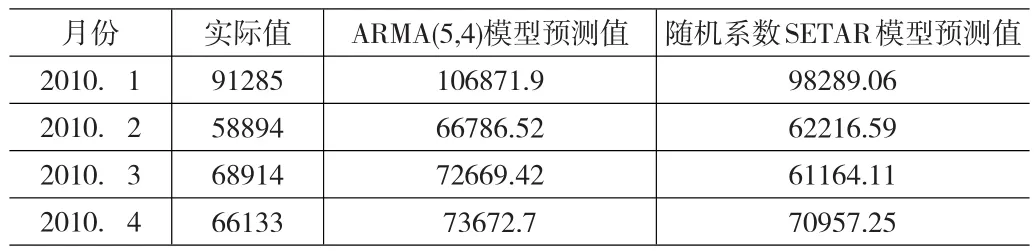
表7
从表6、表7可看出:随机系数SETAR模型无论是拟合程度还是预测结果都要比ARMA(5,4)模型好。
3 结论
本文提出了随机系数SETAR模型回归系数估计的方法,并利用随机系数SETAR模型对一个月度数据进行建模,拓展了SETAR模型的应用范畴,同时还建立了ARMA模型进行比较研究.结果证明随机系数SETAR模型在具有非线性性质的数据序列建模中有较大优势。
[1] 范剑青,姚琦伟.陈敏译.非线性时间序列-建模、预报及应用[M].北京:高等教育出版社,2005.
[2] 安鸿志,陈敏.非线性时间序列[M].上海:上海科学技术出版社,1998.
[3] 袁军.SETAR模型在GDP预测中的应用[J].统计与决策,2007,(5).
[4] 王黎明等.应用时间序列分析[M].上海:复旦大学出版社,2009.
[5] 王振龙等.应用时间序列分析[M].北京:科学出版社,2007.
[6] 赵松山.关于时变参数建模的研究[J].东北财经大学学报,2002,(9).
[7] 李书进,李文华.基于自适应卡尔曼滤波的时变结构参数估计[J].广西大学学报(自然科学版),2004,(6).
[8] 胡琨.基于时变参数模型的创新环境影响研究[J].科技管理研究,2010,(1).
[9] 王宏禹,邱天爽.线性离散系统[M].北京:国防工业出版社,2008.
[10] 韩志刚.多层进阶方法及其应用[M].北京:科学出版社,1989.
