虚拟科研团队网络均衡模型研究

张 宁，杨 帆

（贵州财经学院 信息学院，贵阳 550004）

0 引言

虚拟科研团队的产生和发展代表信息时代中科学研究组织形式的新动向和新趋势，有利于科研资源的灵活配置，有利于提升项目的开发效率[1]，因此，其研究和实践日益得到广泛关注。所谓虚拟科研团队，即是因要完成科研项目而组成的临时性的团队，随着信息技术的发展以及协同观念的产生，科研团队走向了以合作协同为主导，资源共享的联盟形式，这种联盟形式在信息技术的支持下，打破了科研项目在合作过程中的网络和时间的障碍，不在局限于某个特定区域，因此产生了虚拟科研团队的组织形态。

在传统的科研团队构建和管理中，团队各成员间的关系在较长时间内保持稳定，因此团队之间的业务流程接口具有预设定、紧密耦合和良好集成的特点。随着虚拟科研团队的产生，可能存在短暂且不确定性的项目伙伴关系的变化，表明团队各成员间的关系动态性增强，业务接口不是预设的、静态的，而是动态的，难以定义的，即表示团队知识人员和项目组构成多重关系，知识人员能够同时参与多项项目组，产生了流量与建设成本的不确定性，本文即是在考虑人员培训、项目建设成本的前提下，研究虚拟科研团队网络各层次类型知识人员数量的均衡分配资源调度，实现科研项目建设的高效性与优质性。

1 资源调度

资源调度是涉及到资源限制与处理调度的研究，一直以来，广泛存在于生产、交通各个领域[2]。但是国内外的研究表明，各类算法中对人力资源的数量调度和排程在充分考虑各类资源限制的情况下，往往只是针对同一类研究对象，例如同一层次类的人员节点和分布，但在实际的团队活动中，参与同一类项目的团队人员往往也都具有不同的类型，以科研团队而言，在协同合作的过程中，存在多种不同年龄，不同职称，不同知识组织结构层次的知识人员，而不同类型的知识人员在参与项目的过程中，由于经历与经验的差别性，接受培训和建设的层次不同，对项目的贡献程度会产生较大的差异，因此考虑到不同层次类型的知识人员的培训成本与建设费用等因素，比传统只考虑一种类型的人力资源调度排程上要更具有较大的适用范围，也较为科学和合理。

2 建立订单流量均衡模型

虚拟科研团队网络的知识人员动态参与问题可以描述为，多个知识人员参与多项项目，项目的验收时间是预先给定和固定的，调度排程的目的是确定不同项目内不同层次类型的知识人员的数量情况，由于考虑了不同层次结构的知识人员的培训建设成本因素，所以该模型研究培训成本因素影响下的虚拟团队知识人员的数量安排均衡问题。

2.1 符号定义

表1 虚拟科研团队成员数量均衡模型符号定义

2.2 模型定义

在一个稳定长期持续的虚拟科研团队网络内，各类知识人员存在不同的培训成本和建设费用，假设不同类型知识人员的培训费率为yag（a∈M*,g∈G），建设成本费用为βag（如2.1定义所示），则团队成员数量均衡模型可以等价为如下数学规划问题：

其中：

针对不同的知识人员知识结构类型，方程(2)代表了项目组上的知识人员数量和承载负荷成本之间的平衡关系，并保证了所有的数量都是正值，而方程(3)则是代表其中的关联关系，继续有：

对以上数学表达式，假设有：

2.3 算法求解

2.3.1 Frank-Wolfe算法概述[3,4]

F-W算法是Frank和Wolfe于1956年提出求解线性约束问题的一种算法。该方法现在大量用于交通路径分配和规划，属于可行方向法的一种，其基本算法思想是，在每次迭代中，将目标函数线性化，通过线性规划求得下降可行方向，然后再找到一个最优步长，在最速下降方向上截取最优步长得到下一步迭代的起点，进而沿着此方向在可行域内作一维搜索，重复迭代直至找到最优解为止[5,6]。现经过稍加改进后，用于虚拟科研团队网络多项目上的知识人员数量研究问题，同样具有较好的应用意义。

2.3.2 改进后的F-W算法步骤

（1）初始化

令各类型知识人员的平均培训成本费用初始化为：

（2）更新各类知识人员的培训建设成本如对g类型的知识人员，计算：

（3）寻找可行方向

对每一类型g的知识人员，得到每一类型的人员数量并设

（4）计算迭代步长

用二分法求解一维极小问题

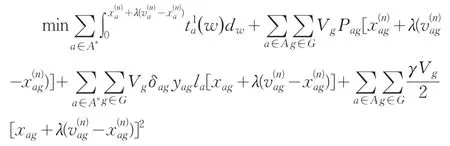
Subject to 0≤λ≤1令其解为λn。

（5）更新项目组上的知识人员数量计算：

（6）检验收敛性

3 结论

随着科学研究和科学活动逐步走向国际化和信息化，研究工作人员对知识获取需求的多元化和深度化，单一成员结构模式的科研组织形态势必不能满足现状，科研团队也需要向着定制和敏捷的方向发展，开放式的虚拟科研团队正是可以帮助科研模式由笨拙走向灵活，打破行政职能的限制，甚至是地域、国别的限制，形成开放式的动态组合的虚拟科研团队，达到科研资源优势互补和有效合作。

及时准确且人力资源分配均衡的虚拟科研团队知识人员调度排程对科研项目的高效运行有着极其重要的影响，是实现团队知识人员调度的合理化和集成化的重要环节。研究多层次类型下多项目资源的知识人员数量均衡模型，考虑到了不同类型知识人员的培训建设成本因素，给出了模型的求解算法，使得该模型更具有广泛和合理的适用范围。

[1] 华荷锋.高校科研团队研究:基于虚拟团队的概念[J].现代教育科学，2005,(4).

[2] 张宁.混合资源调度的遗传算法研究[J].贵州大学学报自然科学版，2009,(2).

[3] 徐裕生，陈诚，史向平.一类几何规划的Frank-wolfe算法[J].河南科技大学学报（自然科学版），2008,(29,1).

[4] 李峰,王书宁.基于Frank-Wolfe算法的路径交通量求解方法[J].吉林大学学报（工学版），2005,(6).

[5] Yin Y F.Genetic-algorithms-based Approach for Bilevel Programming Models[J].Journal of Transportation Engineering,2000,(126).

[6] Anthony Chen,R.Jayakrishnan，Wei K.Tsai.Faster Frank-Wolfe Traffic Assignment with New Flow Update Scheme[J].Journal of Transportation Engineering,2002,128(1).