光伏并网功率调节系统的输出电流无静差跟踪控制*

周龙华 王 飞

(1.中山大学电力电子及控制技术研究所，广东 珠海 519082； 2.中山大学数学与计算科学学院，广东 广州 510275)

传统的化石能源日渐枯竭，发展可再生能源是能源发展的必由之路。太阳能是未来人类最值得依赖的可再生能源之一，而光伏并网发电是利用太阳能的主要形式。另一方面，随着电力电子技术的飞速发展，各种电力电子装置得到广泛的应用，但是也给电力系统带来了严重的谐波污染，有源电力滤波器(Active Power Filter, APF)是改善电网电能质量的一种有效手段[1-2]。光伏并网发电装置与APF 在结构、功能和控制策略上都非常相似，因此可以实现光伏并网发电装置和电能质量治理装置的统一控制。文献[3]将光伏并网发电与有源滤波的一体化装置称之为“光伏并网功率调节(Photovoltaic Grid-connected Power Conditioning, PVPC)系统”。

在PVPC 系统中，电流控制是根据并网电流指令去控制并网逆变器功率开关器件的通断，从而将光伏阵列产生的电能注入到电网中，同时进行无功补偿和谐波抑制，并网电流的跟踪控制是整个系统的重点。文献[3]利用常规比例积分控制器来实现输出电流跟踪，但是输出电流指令信号是以电网频率变化的正弦信号，所以常规的比例积分控制调节器不能消除系统的稳态误差。而文献[4]提出基于重复和电网电压前馈控制相结合的复合控制策略，有效改善了并网电流，但是该控制策略算法复杂，目前仅限于仿真理论研究，并不适于实际工程。文献[5]指出电网中的电压谐波是影响逆变器输出并网电流的主要因素。因而为了提高系统并网电流的跟踪性能和并网电流质量，消除电压谐波的影响，本文根据系统的传递函数，对并网电流闭环进行优化，引入广义积分器，抑制电网电压的影响，实现并网电流的快速无静差跟踪。

1 PVPC系统及其数学建模

在光伏并网功率调节系统中，光伏阵列直接或者经过升压接到APF的直流电容侧，通过最大功率跟踪(MPPT)实现光伏阵列以最大的功率向电网注入有功电能。这样，在进行光伏并网发电的同时不但不会影响APF 的所有功能，反而利用光伏阵列输出电能，增强了直流母线电压的平衡能力P[6]。

为了能同时实现并网发电和非基波有功电流补偿，PVPC 系统的主电路采用电压源逆变器[7-8]。忽略交流电网的内阻抗；并网电抗器，并网变压器与PVPC 内阻等效为R，直流母线的电压为Udc，可以得到三相PVPC 系统的等效拓扑结构如下图1所示。其中ij(j=a，b，c)、ilj(j=a，b，c)和icj(j=a，b，c)分别为电网电流，负载电流和逆变器并网电流；ej(j=a，b，c)为电网电压。

图1 PVPC系统的等效拓扑结构图

在图1中，O′为三相交流电网的中性点，O为直流侧的参考地。假定三相交流电网电压对称且为正序，由电压电流关系，又O与O′等电位，可知在图1中，Ujo为逆变电路输出电压，有

μjo=μjo′=L(dicj/dt)+Ricj+ej；(j=a，b，c)

(1)

对上式进行拉普拉斯变换，可以得到

Icj=(1/(R+sL))(Ujo-Ej)；(j=a，b，c)

(2)

由上式可知，在三相交流电网电压ej一定的情况下，电流icj的幅值和相位都仅决定于逆变器交流侧输出电压ujo中基波分量的相位及其与ej的相位差。而并网逆变器的输出电压ujo是通过调整逆变器功率器件的占空比和直流母线的电压乘积来实现的，所以通过调节逆变器功率器件的占空比就可以调节交流侧电压的幅值和相位，从而控制PVPC系统交流电流的输出和跟踪。

2 PVPC系统动态结构分析

2.1 PVPC系统动态结构分析

由式(2)得到并网逆变器主电路的输出电流icj与电压ujo的传递函数Gm(s)为

Gm(s)=Icj/(Ujo-Ej)=1/(R+sL)

(3)

在图1中，指令电流的跟踪采用SPWM脉宽调制方法时，电压响应会较慢，滞后时间表示为τs，与载波周期Ts相等。Kpwm表示主电路的电压增益，逆变电路的传递函数Gp(s)为

Gp(s)=Kpwm/(τss+1)

(4)

为了能使并网逆变器输出电流跟随指令电流，常规的一般使用前向通路串联的校正装置PI反馈控制，结合各个环节的传递函数，就可以得到电流闭环反馈控制的动态结构如图2所示。

图中，I*(s)为输入指令电流信号，电网电压E(s)为扰动信号，Ic(s)为主电路电流输出信号，kf为电流反馈系数。前向通路串联的校正装置是PI控制环节，其传递函数表示为：

G1(s)=(Kps+K1)/s

(5)

2.2 电网电压扰动前馈补偿

电网电压扰动相当于稳定的外部电压扰动，并存在一定的畸变，所以电网电压扰动的影响较大。电网电压扰动信号e(s)是可测的，所以在开环控制的扰动前端通道中加入反馈，使e(s)通过一个传递函数Gn(s)对ic(s)进行补偿，可以达到消除扰动影响的目的P[9]。如下图3就是电网电压扰动前馈补偿的控制图。

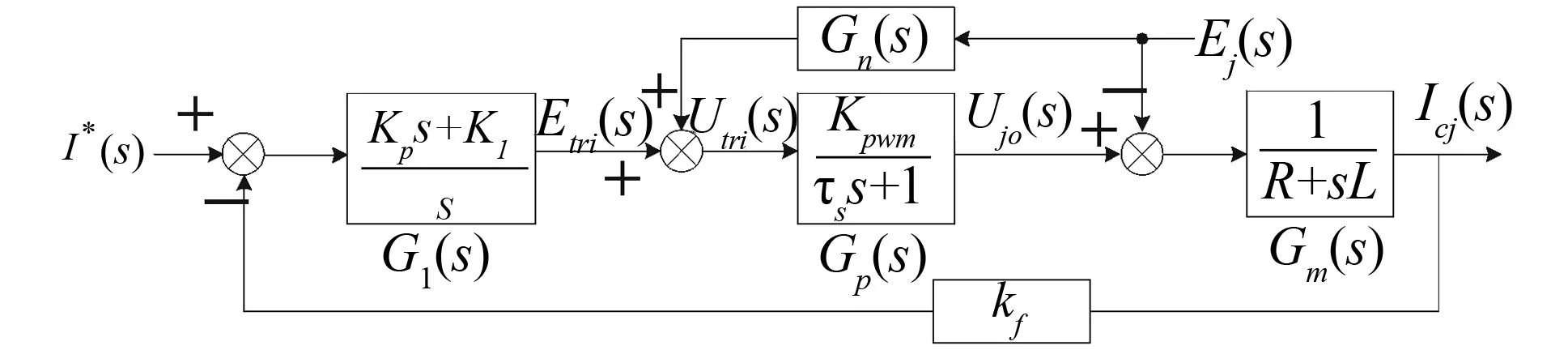
图3 电网电压扰动前馈补偿控制图

此时电网电压扰动对系统输出电流的影响为：

(6)

当Gn(s)=1/Gp(s)时，电网电压扰动e(s)对系统输出电流ic(s)的影响为零，也是实现电网电压扰动全补偿的条件，这样就可以减小电流指令信号，减轻电流调节器的工作量，取得良好补偿效果，大大减小电网电压扰动的影响，增加了系统的稳定性。

3 基于电流无静差跟踪的控制技术

3.1 电流闭环的简化及PI控制

由于采用电网电压前馈控制，补偿了电网电压扰动对输出电流的影响，所以图3的电流闭环控制可以简化为不含电网电压扰动的环节。电流检测信号中常含有噪声和高频分量，所以电流检测电路通常含有低通滤波器来滤除高频分量和尖峰毛刺，设计低通滤波器的滤波时间常数为τf，滤波环节会给反馈信号带来延时，为平衡这一延时，通常在给定信号的前向通道中加一个相同时间常数的给定滤波环节。把加入和补偿的滤波惯性环节等效地移到开环通道，PWM输出滞后时间τs和滤波器滞后时间τf都L/R比小得多，所以，pwm控制滞后时间τs和滤波器滞后时间τf可以近似看做是同一个滞后环节，可以得到电流闭环简化图如图4所示。

图4 简化后的电流闭环

在本文PVPC系统中，图4中所示的电流闭环结构的各参数意义及数值如下pwm控制滞后时间τs=0.05 ms；主回路等效内阻R=0.05 Ω；主回路等效电感L=2.8 mH；电流反馈系数kf=0.04；主电路的电压增益系数Kpwm=100；滤波器滞后时间τf=0.01 ms。

若校正装置G1采用比例积分控制时，则校正后的系统开环传递函数为

(7)

采用比例积分控制时，系统的闭环传递函数Φ(s)=Gopen/(1+Gopen)，则系统的特征方程为

R(τs+τf)s3+[(τs+τf)L+R]s2+

(L+KpwmKpkf)s+KpumKpkf=0

(8)

只要比例积分系数均为正值，则三阶方程的各项系数均为正值，则全部解均为正值，系统是稳定的。所以任意取比例积分系统，如取Kp=1.505 2，Ki=10，可到电流比例积分控制情况下的幅频特性如下图5所示。

图5 电流比例积分控制时的系统开环幅频特性

当信号产生偏差时，PI控制器就立即产生控制作用，相当于在系统中增加了一个位于原点的开环极点，同时也增加了一个位于左半平面的开环零点。位于原点的极点可以提高系统的型别，用来消除或减小系统的稳态误差；而增加的负实零点则用来提高系统的阻尼程度，缓和PI控制器极点对系统稳定性产生的不利影响。

3.2 基于电流无静差跟踪的控制技术

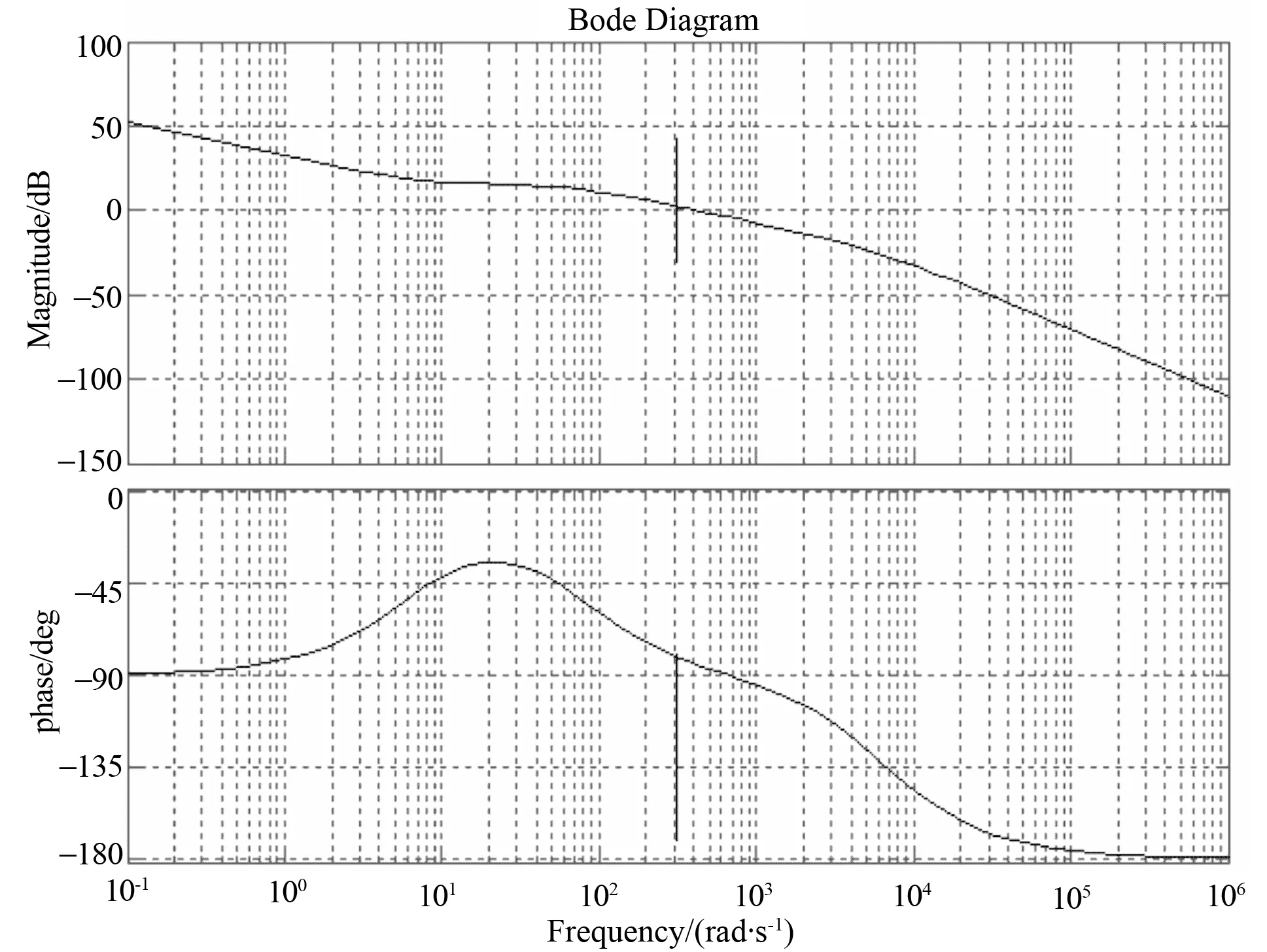
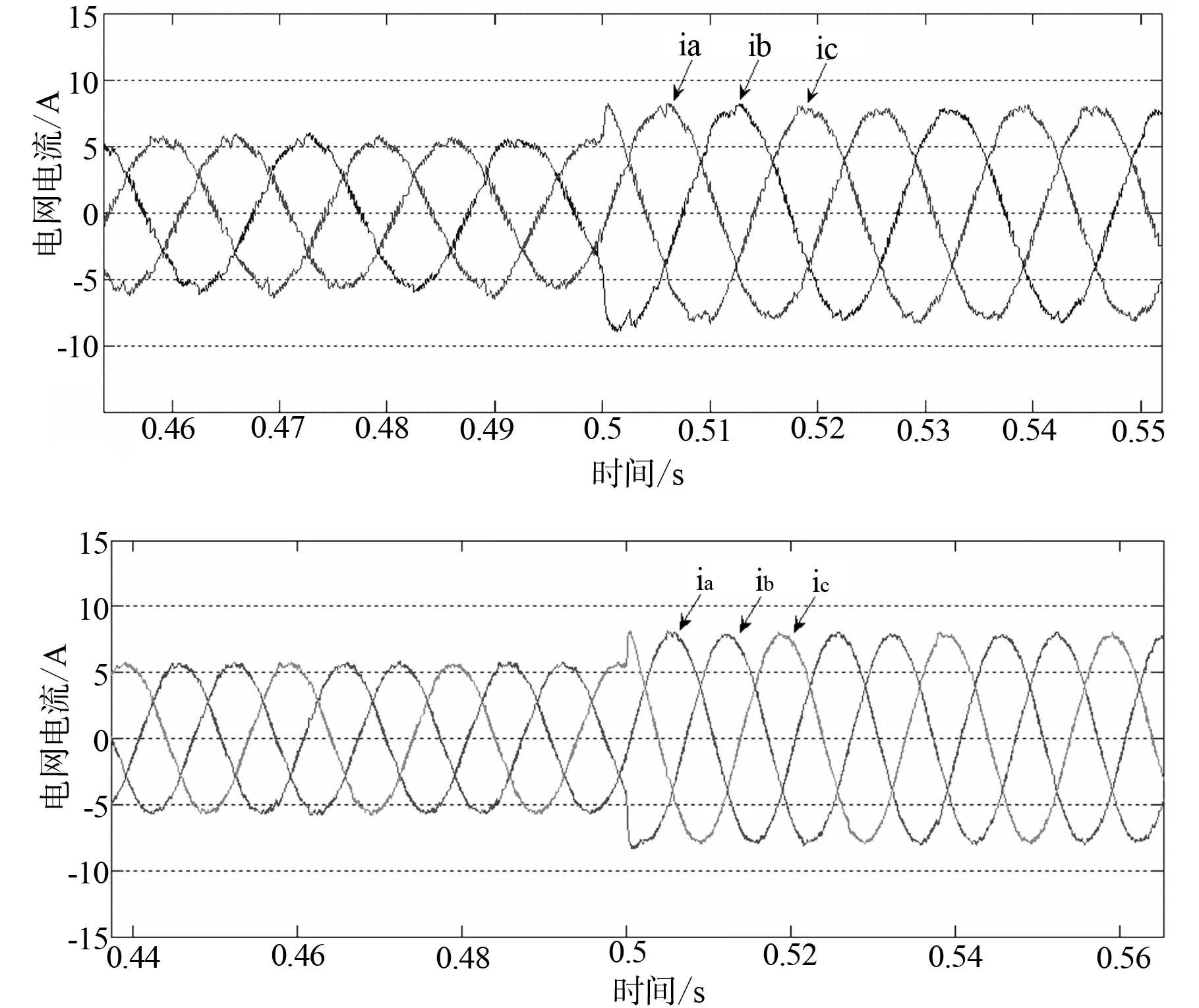
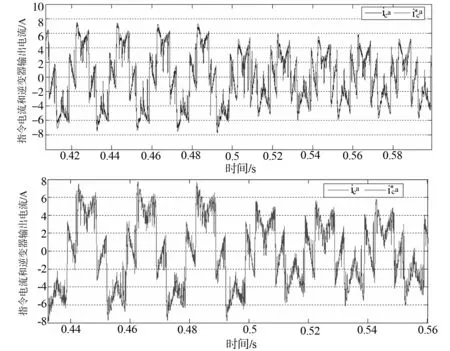
稳定系统的正弦稳态响应有如下结论[10]：当频率为ω0的正弦信号输入到稳定的线性定常系统G(ω)时，正弦稳态响应是一个与输入信号同频率的正弦信号，但幅度变为原来的|G(ω0)|倍，相位增加了

图6 引入广义积分器的系统控制框图

若取Kp=1.505 2，Ki=10，Kω=1电流指令信号最低频率为电网电流基波频率50 Hz，则ω=314 rad/s，系统的开环传递函数为

(9)

其幅频特性如下图7所示。

图7 电流无静差跟踪控制时开环系统的幅频特性

图7电流无静差跟踪控制时开环系统的幅频特性可知，增加了广义积分器的校正装置以后，显著地改变了频率ω=2πf处的幅频特性，开环传递函数的增益大大增加，相当于在谐振频率处串联了一个高增益环节，使得电流实现无静差跟踪。

令E(s)为误差信号，Es(s)为系统误差信号，则图7(b)所示的闭环传递函数为

(10)

令s=jω，上式得φ(s)=1，说明系统输出信号Icj(s)可以稳定地跟踪输入信号I*(s)，所以系统误差信号Es(s)可以表示为

令s=jω，上式得Es(s)=0说明系统电流达到无静差跟踪，此时，电网电压对系统输出的影响为

令s=jω，上式得EG(s)=0，说明此时电网电压对系统输出的影响几乎为0。

4 仿真与实验分析

为了验证上述控制方法的合理性以及实用性，在Matlab/Simulink环境下设计了PVPC系统及其控制系统的仿真平台，然后在光强变化条件的工况下对PVPC系统进行仿真，并对其结果进行分析。另外制作了一台10kW的PVPC系统实验样机，试验结果同样可以验证控制方法的合理性以及可靠性。

太阳电池的模型参照文献[12]，在仿真模型中，非线性负载用二极管整流桥代替，仿真模型的主要参数如下：光伏阵列(Pmax=2 774.52 W;Voc=672 V;Isc=5.50 A;Vmp=550.5 V;Imp=5.04 A;)，非线性负载阻抗(Ll=1 mH;Rc=50 Ω)，并网逆变器交流侧并网阻抗(Lc=5 mH;Rc=0.01 Ω)。另外在PPC点设计一个RC高通滤波器来吸收因开关通断而引起的高次尖峰谐波，其截止频率约为2 kHz。

图8所示是光照强度变化时电网电流的波形，上图采用常规PI控制技术，下图采用基于输出电流无静差跟踪控制技术。光照强度在0.5 s时从1 000 W/m2变化到600 W/m2，可以看出，光照强度变小时，PVPC系统向电网注入的有功电能减小，电网电流增大。同时可以看出，采用输出电流无静差跟的踪控制技术，PVPC的输出波形质量更高，尤其在光照变化时，能迅速进行跟踪调整。

图8 光强变化条件下的电网电流波形

图9 电流跟踪指令结果

图9是A相指令电流以及逆变器输出电流的比较图。上图采用常规PI控制技术，下图采用基于输出电流无静差跟踪控制技术。从图中可以看出，采用基于输出电流无静差跟踪控制技术的PVPC输出电流基本完美跟踪指令电流，其跟踪能力跟采用常规PI控制技术相比，误差小，跟踪迅速。仿真结果证明了基于电流无静差跟踪的校正技术可以实现并网电流的无静差跟踪，响应迅速。

基于输出电流无静差跟踪的控制技术本质上就是实现输出电流快速跟踪并网指令电流，使得光伏并网逆变器的输出电流的相位与电网线电压的相位基本保持同步。所以要验证基于电流无静差跟踪的控制方法，就可以通过检测光伏并网逆变器的输出电流与电网线电压的相位差来验证，同时也可以通过此方法来检测光伏并网的功率因数。在电网电压约为380 V，线电压峰值约为315 V，频率为50.058 Hz时，测得A相电网电压与并网逆变器a相并网电流的波形如图10所示。

图10 PVPC系统的并网发电功能

从图10可以看出，光伏并网逆变器a相输出电流与A相电网电压之间的相位差约为0.08 ms(也即功率因子角为1.14o)，PVPC系统在光伏并网发电时发电功率因素很高，功率因子高达99.96%。并网逆变器输出电流可以实时跟踪并网指令电流，基本实现输出电流的无静差跟踪。并且，光伏并网逆变器的输出电流的波形良好。右图是并网逆变器a相输出电流的谐波频谱分析图，由图同样可以看出，PVPC系统在光伏并网发电时发电功率因数很高，并网电流的谐波含量很少，尤其是高次谐波。

图11是PVPC系统投入前后电网电流的谐波频谱分析，从图中可以看出，在PVPC系统投入后，下图中，电网电流的总谐波畸变率大大减小，高次谐波都抑制在一个很低的水平。而在实际的三相三线系统中，5次和7次谐波通常是最为突出的低次谐波，由图比较可得，5次和7次谐波明显减少。

图11 PVPC系统投入前后电网电流的频谱分析

5 总 结

在PVPC 系统中，电流控制的主要任务是根据并网电流指令去控制功率开关器件的通断，从而将光伏阵列产生的电能注入到电网中，同时进行无功补偿和谐波抑制，因而并网逆变器输出电流的跟踪控制是整个控制系统的重点。文章提出并网电流的快速无静差跟踪控制方法，提高了系统并网电流的跟踪性能和并网电流质量。仿真和实验结果都证明了该控制方法的合理性，可靠性和实用性。

参考文献：

[1] AKAGI H， NABAE A， ATOH S. Control strategy of active power filters using multiple voltage-source PWM converter[J]. IEEE Trans. on Industry Appl., 1986, 22(3): 460-465.

[2] 王兆安, 杨君, 刘进军，等. 谐波抑制和无功功率补偿[M].2版. 北京: 机械工业出版社, 2005.

[3] 汪海宁, 苏建徽, 丁明，等. 光伏并网功率调节系统[J]. 中国电机工程学报, 2007, 27(2): 75-79.

[4] 郑诗程, 刘伟. 光伏并网发电系统及其控制策略的研究与仿真[J]. 系统仿真学报, 2009, 21(19): 6161-6165.

[5] ABEYYASEKERA T, JAHNSON C M, ATKINSON D J, et al. Suppression of line voltage related distortion in current controlled grid connected inverter[J]. IEEE Trans on PE, 2005, 20(6): 1393-1401.

[6] 陈晓高, 付青, 余世杰. 基于自抗扰控制的光伏并网功率调节系统[J]. 中山大学学报：自然科学版, 2009, 48(2): 49-53.

[7] KUOYeongchau , LIANGTsorng juu , CHENJiannfuh . A high-efficiency single-phase three-wire photovoltaic energy conversion system[J]. IEEE Trans Ind Appl, 2003, 50(1): 116-122.

[8] TAN P C, JUSOH A, SALAM Z. A single-phase hybrid active power filter connected to a photovoltaic array[C]∥ The 3rd IET International Conference on Power Electronics, Machines and Drives, 2006: 85-89.

[9] SHIMIZU T, WADA K,NAKAMURA N. A flyback-type single phase utility interactive inverter with low-frequency ripple current reduction on the DC input for an AC photovoltaic module system[C]∥ IEEE Proc of 33rdAnnual PESC, 2002, 3:1483-1488.

[10] 顾绳谷. 电机及拖动基础[M]. 北京: 机械工业出版社, 1992.

[11] 唐欣, 罗安, 谭甜源. 有源电力滤波器的比例递推积分控制[J]. 控制理论与应用, 2004, 21(4): 631-634.

[12] 茆美琴, 余世杰, 苏建徽. 带有MPPT功能的光伏阵列Matlab通用仿真模块[J]. 系统仿真学报, 2005, 17(5): 1248-1251.