基于GBMMAS算法的“风-光”互补系统容量优化研究*

谢 磊，王 飞，余世杰，陈晓高

(1.中山大学数学与计算科学学院，广东 广州 510275;2.中山大学物理与工程技术学院，广东 广州 510275)

“风-光”互补系统的出现为偏远地区及海岛居民的用电提供了一条合理、有效的途径。其充分利用了风、光资源在时间及地域上的互补性，能够在有效降低系统成本的同时提高系统供电可靠性。目前运行的“风-光”互补系统中普遍存在组件容量设计不合理的现象，造成系统供电可靠性低、成本过高等问题，因此需要对系统组件容量进行优化。在“风-光”互补系统中，组件的不同容量组合会对系统的性能表现产生重要影响，属于组合优化中典型的NP-hard问题，对此问题可应用蚁群优化算法进行求解[1-2]。本文提出了一种基于有向图思想的“最大-最小”蚂蚁系统算法，在满足一定负载失电率(LPSP)的前提下，对系统能量均摊成本(LCE)进行优化，从而得出系统各组件的容量大小。

1 系统结构及工作原理

图1所示为本文中所研究的“风-光”互补系统的结构，其主要工作原理如下。

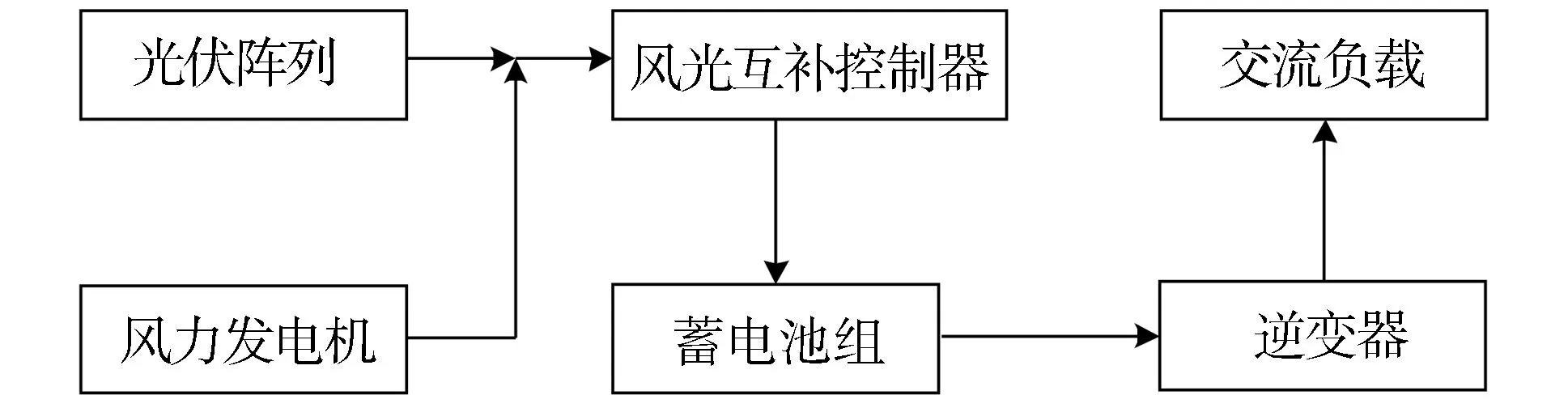
图1 “风-光”互补系统的结构

由光伏阵列和风力发电机所产生的电能经过风光互补控制器后向蓄电池组充电，蓄电池组在储存电能的同时经过逆变器(直流-交流)向交流负载供电。

2 负载失电率LPSP和能量均摊成本LCE

在“风-光”互补复合能源供电系统中，评价整个系统性能表现的主要指标是供电可靠性和系统成本。对这两项指标的评估是通过计算负载失电率LPSP和能量均摊成本LCE这两个参数来实现的。

2.1 负载失电率LPSP

负载失电率LPSP被定义为在运行周期内，系统亏欠负载的电量与评估期内负载所要消耗的总电量的比值[3-4]：

(1)

系统在t时刻亏欠负载的总电量LPS(t)为[5]

LPS(t)=PLoad(t)Δt-(PPV(t)+PWT(t))Δt·ηinv-

Cbat·(SOC(t-1)-SOCmin)·ηinv

(2)

式中，PLoad为负载功率需求，W；PPV(t)为t时刻由光伏阵列产生的功率，W；PWT(t)为t时刻由风机产生的功率，W；Cbat为蓄电池组额定容量，Ah；SOC(t-1)为蓄电池组在t-1时刻的荷电状态；SOCmin为蓄电池组允许的最小荷电状态；Δt为时间步长，h；ηinv为逆变器效率，本文取90%。

2.2 能量均摊成本LCE

能量均摊成本LCE由下式定义[6-7]

LCE=Ctotal×CRF/ELoad

(3)

式中，ELoad为系统每年向负载提供的电量，kWh；Ctotal为系统中所有组件的总成本，￥；CRF为投资回报系数。Ctotal和CRF可分别通过下式计算[8]：

Ctotal=Ctot-PV+Ctot-WT+Ctot-bat

(4)

(5)

式中，i为利息率，本文取8%；n为系统寿命，年；Ctot-PV、Ctot-WT为分别为光伏组件、风机的初期投资和维护成本，￥；Ctot-bat为蓄电池的初期投资和更换成本，￥。

2.3 组件容量大小对LPSP和LCE的影响分析

根据图1所示系统结构，在负载对供电可靠性有一定要求的前提下，可将组件容量对LPSP和LCE的影响分为以下3种情况：

1)组件容量设计过剩：此时LPSP虽满足要求，但LCE将很高，系统经济性差。且随着组件容量的增大，LPSP呈减小趋势，LCE呈增加趋势。

2)组件容量设计不足：此时LCE虽然低，但由于LPSP不满足要求，系统的供电可靠性差。且随着组件容量的减小，LCE呈减小趋势，而LPSP呈增加趋势。

3)组件容量设计良好：此时LPSP满足要求，且LCE也不高，系统经济型和供电可靠性佳。

3 基于有向图思想的“最大-最小”蚂蚁系统算法的实现

本文所研究的“风-光”互补系统组件容量优化问题是一个背包问题[9-10]，该问题的实质即是从一个由多个风机、光伏组件和蓄电池构成的集合中，选取其中一部分组件构成子集，使得该子集在满足一定LPSP的约束条件下，系统LCE最低。基于此，本文提出了一种基于有向图思想的“最大-最小”蚂蚁系统(GBMMAS)算法[11-12]，在满足一定LPSP的前提下，对系统LCE进行优化：

目标函数：

(6)

约束条件：

LPSP≤LPSP*

(7)

解限制条件：

min{NPV_p,NWT,Nbat_p}≥0

(8)

式中，LPSP*为LPSP给定值；NPV_p为光伏组件并联数量；NWT为风机数量；Nbat_p为蓄电池组并联数量。

下面介绍将有向图思想应用于优化本文所研究系统的原理：将系统在满足LPSP条件下最小LCE所对应的组件容量的求解视为蚁群在巢穴和食物之间觅食最短路径的选择。将系统各组件作为求解路径中的节点，组件数量大小对应于蚁群在觅食中的路径长度，这样即可将对此问题的求解转化为TSP问题的求解。由此可构建有向图：

G=(N,A)

(9)

式中，N为结点的数量；A为路径的数量。

令R为在有向图G中满足下列条件的所有路径r的集合：

1)所有蚂蚁均从起始节点0开始移动，即从同一起始点进行“路径”的构建；

2)在每条“路径”中，各节点只能出现一次。

由上述条件对本文中“路径”上节点设置如下：

{节点0 节点1 节点2 节点3}=

{起始点 光伏阵列 风机 蓄电池}

基于上述思想，本文中GBMMAS算法的流程如下(参见图2)。

1)初始化参数：蚂蚁数量m=40，最大迭代次数Ncmax=100，迭代计数器n=0，信息量τij(0)=τmax、信息素增量Δτij(0)=0，初始化时信息素上限τmax和下限τmin为[13]：

(10)

(11)

式中，ρ为信息素挥发系数，本文中取ρ=0.2；LCE(n)为第n次迭代后的系统最优LCE，￥/kWh。

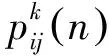
(12)

式中，Ni为表示第i个变量的取值范围；α为信息启发式因子；β为期望启发式因子。本文取α=1，β=4。ηij(n)为表示由节点经由路径j到达下一节点的期望程度：

(13)

式中，Ci为表示第i个节点对应的设备单价，￥；Vj为路径j上设备的数量。

为满足每条“路径”中各节点只能出现一次的限制条件，算法中需要添加“禁忌表”，即将蚂蚁走过的节点放入表中，蚂蚁k在访问下一节点时不能访问表中已有节点，直至所有蚂蚁完成对所有节点的访问后将禁忌表清空。

3)本文中对信息素的更新采用MMAS算法：

(14)

(15)

式中，LCE=min(LCEk)，k=1,2……m。

5)当群体中的最优个体满足一定要求或迭代次数达到Ncmax时，优化结束，否则转入第2步进行操作。

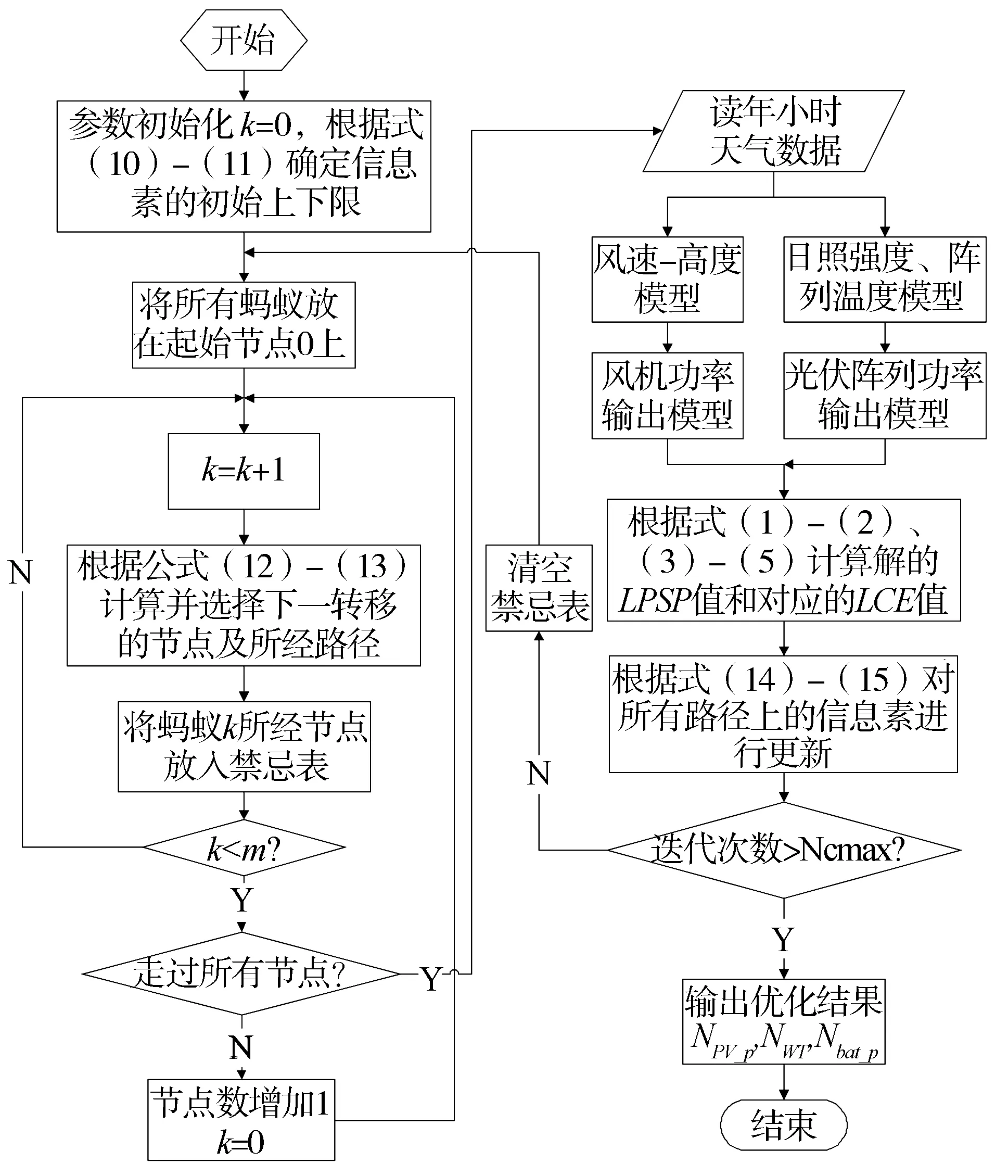
图2 GBMMAS算法流程图

4 运算结果及分析

本文采用了珠海地区2007年12月份中50个点的年小时气象数据(风速、日照强度和环境温度，见表1)，并利用Matlab中的M语言编制了GBMMAS优化算法，在给定LPSP*=2%的约束条件下对系统中风机、光伏阵列及蓄电池组的容量进行了优化。算法中节点1、2、3分别代表风力、光伏组件和蓄电池组的设备编号，而路径长短则分别代表这三者的数量。

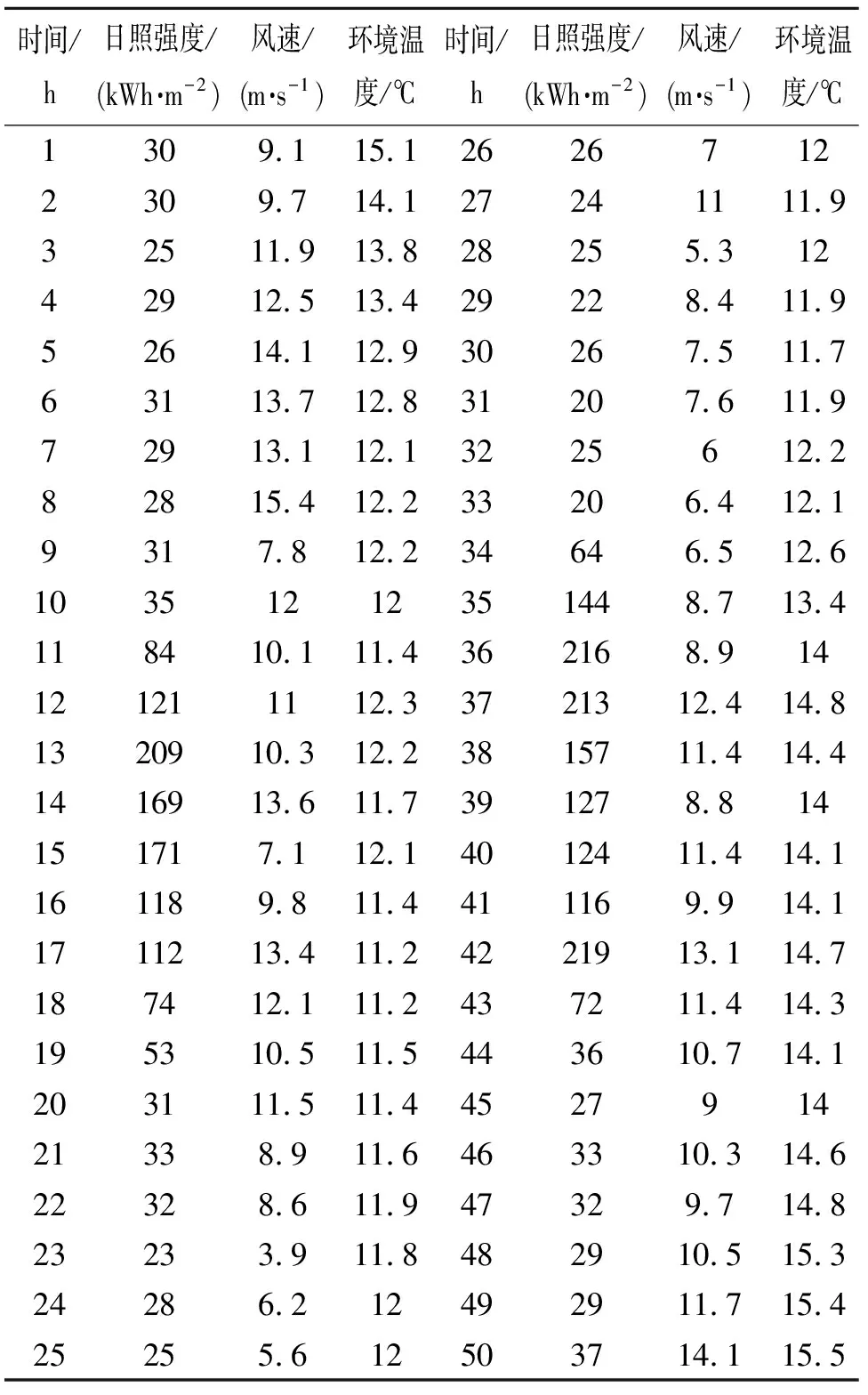
表1 珠海地区07年12月气象数据

表2、表3及表4分别为系统优化中选用的风机、光伏阵列及蓄电池的规格及参数。由于本系统中直流母线电压为24 V，可知蓄电池组需采用8串结构。优化中系统负载大小设定为5 kW。为了观察本文所提出优化算法的执行效率及稳定性，本文进行了50次算法优化运算，并记录了每一次解收敛时的算法迭代次数，结果如表5所示。

表2 光伏组件S-125C参数

表3 蓄电池GMF-500C参数

表4 BWC XL.1风力发电机运行参数

表5 50次优化过程中收敛解的迭代次数

经统计，本文所设计的GBMMAS优化算法在收敛时所经历的平均迭代次数为16次，可以看出该优化算法在对“风-光”互补系统进行系统配置优化时算法的运算效率很高，经过一定次数的迭代后LCE均收敛于0.664 9处。图3为算法收敛时解的迭代次数在0-100的概率分布。

图3 迭代次数的概率分布

由图可知，迭代次数在0-20次之间的概率为0.82，这与16次的平均迭代次数是一致的，也充分说明算法是稳定的，而迭代次数在0-10次之间的概率为0.62，说明算法在绝大多数情况下是很快就可以达到收敛的。

图4 所示为其中一次的GBMMAS算法的系统优化过程。对应于该优化过程的系统组件容量优化结果为：

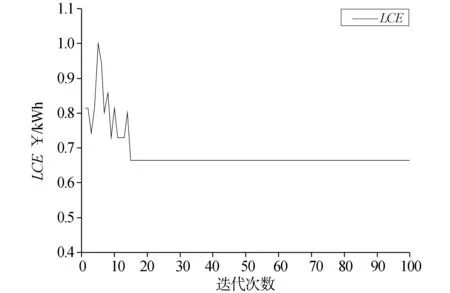
图4 GBMMAS算法的优化过程

1)节点：0—2—1—3，代表蚂蚁的寻优所经节点顺序为：0—光伏组件—风机—蓄电池组。

2)路径：0—1—7—1，根据节点中的设备号可知，光伏组件的并联数量为1，风机的数量为7，蓄电池组的并联数量为1。表6即为系统优化结果。

表6 LPSP*=2%时系统优化结果

5 结 论

本文针对目前运行的“风-光”互补系统中普通存在的系统配置不合理的现象，提出了一种基于有向图思想的“最大-最小”蚂蚁系统算法，用于对“风-光”互补系统的配置优化。并运用该优化算法对系统成本及组件的容量进行了优化。运算结果的分析表明，本文所设计的优化算法稳定性高，并且在多次运算过程中均可以很快达到收敛，算法的执行效率很高，得出的优化结果是合理的。

参考文献：

[1] NOUREDDINE Liouane, IHSEN Saad, SLIM Hammadi, et al. Ant systems & local search optimization for flexible job shop scheduling production[J]. International Journal

of Computers, Communications & Control, 2007, 2(2):174-184.

[2] 罗中良, 易明珠, 周有平. 基于智能混合算法的经济调度问题及其参数调整方法[J]. 中山大学学报:自然科学版, 2008,47(1):33-37.

[3] YANG H X, LU L, BURNET J. Weather data and probability analysis of hybrid photovoltaic-wind power generation systems in Hong Kong[J]. Renewable Energy, 2003, 28(11):1813-1824.

[4] DIAFA S,BELHAMELB M,HADDADIC M. Technical and economic assessment of hybrid photovoltaic/wind system with battery storage in Corsica island[J]. Energy Policy, 2008, 36(2):743-754.

[5] AI B, YANG H, SHEN H, et al. Computer-aided design of PV/wind hybrid system[J]. Renewable Energy. 2003, 28(10):1491-1512.

[6] NELSON D B, NEHRIR M H, WANG C. Unit sizing of stand-alone hybrid wind/PV/fuel cell power generation systems[J]. IEEE Power Engineering Society General Meeting, 2005,3: 2116-2122.

[7] DIAF S,NOTTON G,BELHAMEL M.Design and techno-economical optimization for hybrid PV/wind system under various meteorological conditions[J].Applied Energy,2008,85(10):968-987.

[8] YANG H X,ZHOU W,LU L.Optimal sizing method for stand-alone hybrid solar-wind system with LPSP technology by using genetic algorithm[J].Solar Energy,2008,82(4):354-367.

[9] 罗小虎, 赵雷. 一个解决0/1背包问题的蚁群方法[J]. 苏州大学学报:工科版, 2004, 24(1): 41-44.

[10] KONG M,TIAN P,KAO Y CH.A new ant colony optimization algorithm for the multidimensional Knapsack problem[J].Computers & Operations Research,2008,35(8):2672-2683.

[11] GUTJAHR W J. ACO algorithms with guaranteed convergence to the optimal solution[J]. Information Processing Leters. 2002, 82(3):145-153.

[12] GUTJAHR W J. A generalized convergence result for the graph-based ant system metaheuristic[J].Probability in the Engineering and Informational Sciences,2003, 17(4):545-569.

[13] 汪定伟. 智能优化算法[M].北京：高等教育出版社, 2007:200.