一类随机微分方程的轨道唯一性*
2011-07-24赵辉艳
赵辉艳
(中山大学数学与计算科学学院,广东 广州510275)
考察方程

(1)
其中σ:Rd→Rd⊗Rm和b:Rd→Rd为连续函数,W为布朗运动。众所周知,如果σ和b满足Lipschitz条件或者满足局部Lipschitz条件和线性增长条件,则方程(1)具有唯一的强解[1-2]。之后,Watanabe等[3]在方程为一维的情况下在更弱的条件下得到方程解的轨道唯一性的,即方程系数满足一定意义下最弱的Hölder连续性。最近,在方程的系数σ为常数或b=0的情形下,方程在更弱的条件下具有解的存在唯一性得到了讨论。当方程的系数均非常数时,文献[4]中给出了一个解的存在唯一性的充分条件,之后[5]中又做了稍许的推广。
另一方面,根据Airault-Ren[6]和Malliavin[7]的工作,研究中将会碰到如下的非Lipschitz系数的无穷维布朗运动驱动的随机微分方程
(2)
文献[8]研究了这类的方程在一般非Lipschitz系数下的解的存在唯一性。之后,在文献[9]中,把文献[8]的存在唯一性结果推广到系数更为一般的情形,即
|σ(x)-σ(y)|≤ρ(|x-y|),
|b(x)-b(y)|≤γ(|x-y|)
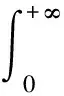
受到了文献[10]的启发,在这篇文章中,我们同样考察方程(2),我们的主要任务是减弱γ的限制,即在某种意义下,把上述的条件中γ的凹性去掉。
1 基本记号及假设条件
假设σi(x),i=1,2,…和b(x)为R→R的可测函数。考虑下述的随机微分方程
(3)
其中Wi,i=1,2,…为一串独立的标准的布朗运动序列。记
σ(x)=(σ1(x),σ2(x),…),
另外假设对所有的x∈R,有σ(x)∈l2。
我们将不加证明地陈述几个无穷维布朗运动的随机微分方程的性质,若需要证明,请查看文献[8-9]。
引理1 假设(Ft)为由布朗运动Wi(i=1,2,…)生成的自然流。假设Hi(i=1,2,…)为一串Ft可测适应过程。如果对所有的t≥0,有


为连续的L2鞅。如果对所有的t≥0,有

那么M为连续的局部鞅。如果Gi(i=1,2,…)为一族Ft可测适应过程,且
则M和N的交互变差过程为
我们有下述的Yamada-Watanabe定理。
定理1 方程(3)有唯一强解当且仅当存在弱解和轨道唯一性。
若需要了解更多的关于方程(3)的强解和弱解,请参看文献[9]。我们还有如下结果[9]。
命题1 方程(3)存在一弱解如果σ和b为有界连续函数。
2 主要结果
定理2 假设γ∈C1((0,1])为严格正的函数并且满足
(4)
并且对任意的a>0,满足
对|x-y|<1,假设
|b(x)-b(y)|≤c|x-y|γ(|x-y|)
我们假设严格正函数ρ满足
(5)
另外假设,对所有的x,y∈R,有
|σ(x)-σ(y)|≤ρ(|x-y|)
则方程(1)具有轨道唯一性。



假设
事实上,在(4)式中,以Nγ代替γ,对足够大的N>0。那么就有
(6)
令
和
Φδ(s):=exp(φδ(s)),δ>0,s∈(0,1]
则有

假设Xt,Yt为方程(1)的两个强解。则有



令τ=inf{t>0,|Zt|≥ε},则有



对上式两边同时取期望,得到
gk″(Zs)(σi(Xs)-σi(Ys))2ds)≤1 +
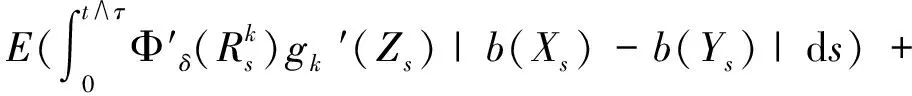

E(Φδ(|Zt∧τ|))≤1 +

根据Gronwall不等式,对每一个δ>0,可以得到
E(Φδ(|Zt∧τ|))≤exp(ct)
令δ→0,则对每一个给定的t,有
|Zt∧τ|=0a.s.
如果有P(τ<+∞)>0,则对某个T足够大,就会有P(τ
根据命题1,我们有下面的推论。
推论1 假设σ和b为有界连续函数并且满足上述定理的条件。则方程 (3) 具有唯一强解。
参考文献:
[1]黄志远.随机分析学基础[M].2版.北京:科学出版社,2001.
[2]IKEDA N, WATANABE S.Stochastic differential equations and diffusion processes [M].2nd ed.Kodansha Ltd, Tokyo, 1989.
[3]WATANABE S, YAMADA T.On the uniqueness of solutions of stochastic differential equations II [J].J Math Kyoto Univ, 1971, 11: 553-563.
[4]FANG S Z, ZHANG T S.A study of a class of stochastic differential equations with non-Lipschitzian coefficients [J].Probab Theory Related Fields, 2005, 132 (3): 356-390.
[5]WANG F Y, WANG J M.Finite and infinite dimensional stochastic differential equations with non-Lipschitzian coefficients [J].Chinese Journal of Applied Probability and Statistics, 2009, 25 (2): 126-134.
[6]AIRAULT H, REN J G.Modulus of continuity of the canonic Brownian motion “on the group of diffeomorphisms of the circle” [J].J Funct Anal, 2002,196 (2): 395-426.
[7]MALLIAVIN P.The canonic diffusion above the diffeomorphism group of the circle [J].C R Acad Sci Paris Sér I Math, 1999, 329 (4): 325-329.
[8]CAO G L, HE K.On a type of stochastic differential equations driven by countably many Brownian motions [J].J Funct Anal, 2003, 203 (1): 262-285.
[9]HE K, ZHANG X C.One dimensional stochastic differential equations with distributional drifts [J].Acta Math Appl Sin Engl Ser, 2007, 23 (3): 501-512.
[10]CHIANG T S, LIN C Y.On pathwise uniqueness of stochastic differential equations [C]∥Proceedings of the 5th Asian Mathematical Conference, Malaysia 2009:687-694.
