普适计算环境下三维模型的错误保护编码*

朱为鹏,罗笑南,3, 梁云

(1．中山大学信息科学与技术学院，广东 广州 510006；2．中山大学数字家庭教育部工程研究中心，广东 广州 510006；3．中山大学深圳研究院∥数字生活网络与内容服务重点实验室，广东 深圳 518057；4．华南农业大学信息学院, 广东 广州 510642)

在普适计算环境下，无线信道是数据传输的主要通路。与有线信道相比，无线信道不仅噪声大，而且具有多径和阴影衰落，误码率高达10-3～10-5(有线信道的误码率一般在10-6以下)[1]。高误码率严重影响数据传输的质量，因此，三维模型编码是否具有很强的抗误码能力是确保三维模型数据传输QoS的关键之一。

同时，为了节省宝贵的网络带宽资源，需要对三维网格模型数据进行压缩。由于预测编码和不定长熵编码等压缩编码方案的使用，三维网格数据压缩效率越高，其压缩比特流对传输错误越敏感。随机或突发的传输错误一旦发生，很可能在压缩编码数据中快速地传播，造成严重的错误蔓延。

目前，关于改善三维网格模型数据误码弹性的研究很少。提高三角网格模型误码弹性所采用的方法主要是通过网格分片或分层等数据分割机制来阻止传输错误的蔓延。如：自适应的网格分割编码等。受限于三维模型不规则的网状拓扑结构，这些方法不仅操作比较复杂，对误码弹性的改善效果也不能令人满意。

为此，本文提出了一种应用于普适计算环境下三维模型压缩传输的错误保护 编码方案。通过将三维网格模型编码为规则采样数据，三维模型网状的拓扑连接关系被隐藏于完全规则的网格结构中，数据关联性大为降低，三维模型的误码弹性得到了根本性改善；同时由于三维模型被均匀采样为二维图像数据，正交分析工具可直接运用，大大提高了压缩效率。

1 相关工作

关于改善误码弹性的研究非常多[2-3]。但针对三维模型数据误码弹性的研究比较少，目前所采用的方法主要是通过网格分片或分层等数据分割机制来阻止错误蔓延超过块边界。如：MPEG-4中采用了基于组件的数据分块策略(Component-Based Data Partitioning Scheme)来提高基于拓扑手术的三维网格模型压缩编码(TS-Based Coding)的误码弹性[4-5]。Li和Kuo[6-7]提出了一种建设性的遍历编码技术，在此基础上，有一些基于网格分割策略的提高网格误码弹性 的研究[8-9]。其后，Yan等[10]提出了多点分块机制(Multi-Seed Based Partitioning Scheme)来控制错误蔓延对压缩的三维网格比特流的影响。Yan等[11]首先将可逆可变长编码技术应用于三角网格编码中。

Gu等[12]在2002年提出了一种构造全规则三角网格模型的重新网格化方法，可得到完全规则的网格模型。但是对于亏格高或有较长突起的模型来，会产生很高的参数化变形。为了减轻这种参数化变形，SANDER等提出了一种将模型参数化到平面上的多个任意边界区域的多片式几何图像构造方法[13]。

2 编码方案概述

本文提出了一种针对任意三维网格模型的均匀准保角平面参数化方法，可建立任意拓扑的三维网格模型与平面参数域之间的均匀准保角映射。再对参数域规则采样，即可将三维模型几何位置信息转化为规则采样的平面信号。

得到三维网格模型的规则采样数据后，结合其自身特点并借鉴压缩视频流抗误码编码技术，本文给出了基于错误保护的压缩编码方法，取得了编码效率和错误弹性之间的平衡。

本文编码方案的主要步骤如图1所示。

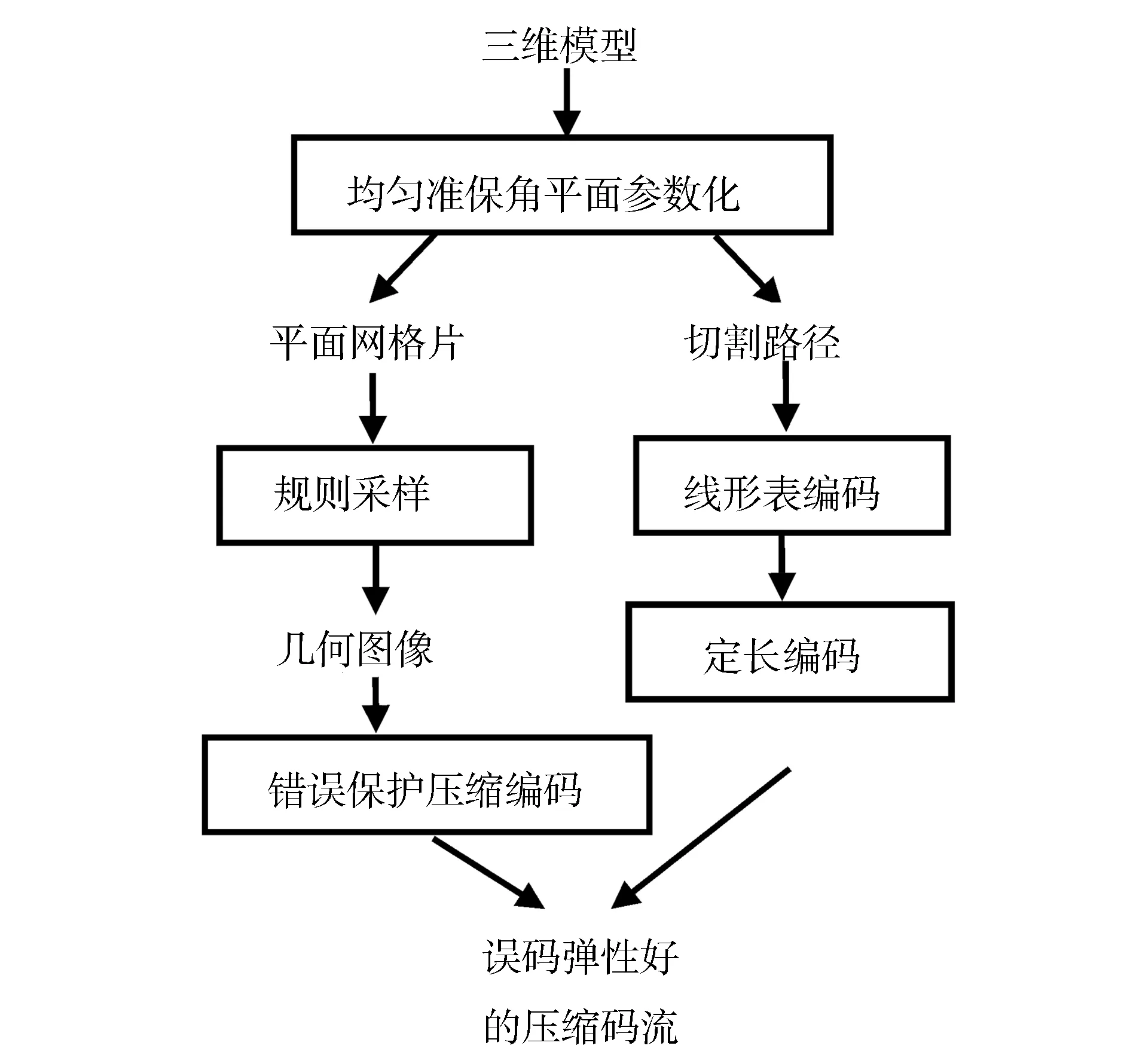
图1 三维模型编码方案流程图

本文第三部分介绍三维模型的均匀准保角平面参数化方法并分析由此所得的三维模型规则采样数据；第四部分介绍对三维模型规则采样数据的所采取的基于错误保护的压缩编码方法；第五部分将本文所述的编码方法应用于不同亏格和复杂程度的三维模型，通过模拟试验得出本文编码方案在误码弹性 和编码效率方面的具体数据。

3 三维模型的规则采样数据

一旦参数化过程中产生较大变形，参数域上均匀分布的采样格点映射到三维模型时不能均匀分布，造成初始三维模型上大量特征丢失，导致规则采样数据因不能忠实重建原始模型而失去价值。只有当参数化变形得到控制，参数域上均匀分布的采样格点才能相对均匀的映射到三维模型(如图2所示)。

图2 参数化变形对采样点分布的影响(红蓝线的相交点即采样点所在位置)

3.1 三维模型的均匀准保角平面参数化

出于尽量降低并控制参数化变形的目的，本文提出了一种均匀准保角平面参数化方法，步骤如下。

首先在初始三角网格模型上随机选取一个非边界的种子三角形，将其保长映射(完全无变形)到平面；然后从该三角形出发，依据局部几何变形度量，每次选取一个变形最小的相邻三角形展平，展平时保证所有三角形不重叠，直到所有相邻三角形引入的参数化变形均大于预设值；再重新随机选取种子三角形进行新一轮的展平，这样每一次展平操作就生成一个新的准可展面片。

衡量局部三角形参数化变形程度时，假定T为原始三角网格模型上的一个三角形，T′为其二维平面上对应的映射，γmax和γmin为仿射变换Jacobi矩阵的最大和最小特征值，对应于原始平面上的不同位置单位长度在仿射变换之后长度的最大值和最小值。根据基于几何变形(Geometric-stretch)度量空间的方法，三角形之间仿射变换的特征值度量空间定义如下

(1)

对于测量几何失真来说，拉伸和收缩应一视同仁，因此Sorkine在文[7]中将局部三角形参数化变形定义改进为

D(T,T′)=max(γmax,1/γmin)

(2)

但这种定义方法仅用最大拉伸或最大收缩作为衡量参数化变形大小的指标，只能近似指示局部三角形角度和面积变形的大小。

考虑到从种子三角形开始的映射是保长的，即γmax与γmin值同为1，与其相邻的三角形均有一条边保持原长，因此，相邻三角形若越近似于保角映射则局部三角形面积和角度的综合参数化变形越小。以此类推，在随后的展平过程中，每一次都是选取参数化变形最小且未超出预定阈值的相邻三角形展平，对整个展平区域的映射可视为准保长，因此，仍可近似认为所有相邻三角形中映射越接近于保角映射，其综合参数化变形越小。

因此，我们定义局部三角形参数化变形为

D(T,T′)=γmax/γmin-1

(3)

当且仅当γmax等于γmin时，由T到T′的映射为保角映射。采用这种参数化变形度量方法，可更好的控制整体参数化误差，保证每一步展开操作后得到准可展面片。

采用这种参数化方法创建规则采样数据及重构三维模型的过程如图3所示

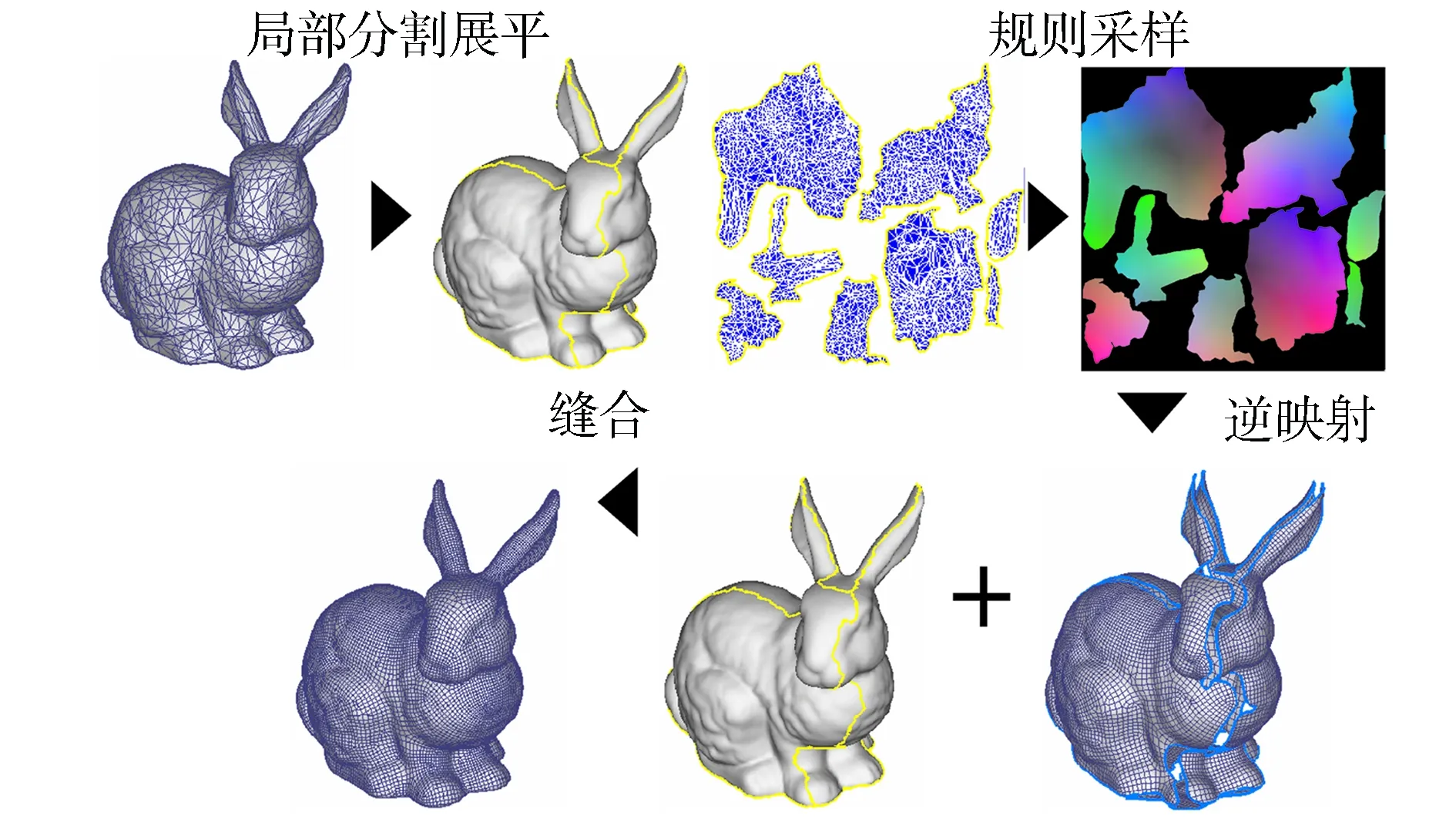
图3 三维模型规则采样数据的创建和三维重构

3.2 几何图像的数据结构

均匀采样点的几何位置信息由一个3×m×n数组来记录。每个数组元素为一个浮点数；而切割路径数据，则采用线性表来记录，每个数据元素对应一个三维空间点，每一段切割路径的结束用一个空数据元素来标记。

由于采用局部分割展平参数化方法，本文创建的几何图像上除了被定义的采样点外，还包含未定义的点。因此我们还需要将未定义的点标识出来。

在区分未定义的点时，基于保持跟普通图像数据在形式上一致同时节省存储空间的考虑，采用的策略如下：设定值(0,0,0)只用于表示未定义的点。即将三维模型包络体上坐标值最小的一个顶点设定为坐标原点，如果该点同时也是网格模型上的一个顶点，就将该点移动到(-Max(x)/1 000,0,0)，并将该点移动后所至的位置作为新的坐标原点。这样就可确保坐标值(0,0,0)不在三维模型的表面。

根据以上分析可知，本文算法所得几何图像的文件结构如下：几何图像文件的第一部分记录网格模型规则采样点的几何位置信息，数据结构为一个3×m×n数组；第二部分记录切割路径信息，数据结构为线性表。除此之外，还可以数组的形式记录规则采样点的其他表面几何信息，如纹理和法向方向等。

3.3 几何图像数据的误码弹性

评价数据误码弹性的主要指标包括数据关联程度和数据相关性。

数据关联是指数据之间相互依赖的程度，即数据的正确解码是否需要依赖其它数据。它是通信错误在数据间扩散造成数据传输质量急剧下降的直接原因。数据编码的关联性越强，其误码弹性越差。

数据相关性是指相邻数据之间的变化比较平滑，并且有一定的规律。它同时也体现了信息在结构上的冗余程度。如果数据相关性强，一旦传输错误发生，在错误隐藏与恢复阶段，就可以利用周围正确传输的数据隐藏数据异常或缺失，较好地恢复正确的数据。

提高误码弹性的关键是降低数据之间的关联程度，同时尽量保持其相关性。以三角网格模型的几种主流文件格式obj, wrl, ply为例：三角网格模型数据文件的主体都是由顶点元素列表和面元素列表两部分组成，其中顶点元素列表记录三维网格模型的几何信息：即各顶点在三维空间的位置；面元素列表记录三维网格模型的拓扑信息，通过列出组成每个三角面片的顶点序号，记录顶点之间的拓扑连接关系。顶点表和面表都是无序的，可随意改变顶点表内元素的排列顺序(面表的内容作相应改变)或面表内元素的排列顺序。因此，三角网格模型数据之间不存在相关性。

同时，面表(拓扑连接信息)的正确解码必须依赖于完全正确的顶点元素列表。如果顶点元素列表的传输出现错误，拓扑连接信息就有可能出错，特别是一旦顶点元素列表的序号出现错误，将导致整个网格结构的破坏。

对于几何图像数据，由于拓扑连接关系被隐藏于完全规则的网格结构，而几何位置信息在均匀采样后，被存储为类似于图像的矩阵方式，具有相邻的矩阵序号的元素对应空间上相邻的点，因此数据之间的相关性较强。

以上对三角网格数据和几何图像数据的数据关联性和相关性的分析结果如表1所示。

表1 几何图像和三角网格数据误码弹性分析

由此可见，将三角网格模型编码转化为几何图像编码后，数据关联程度随之大为降低，同时数据相关性增强。这使得几何图像数据形式在误码弹性上与三角网格数据形式相比有明显的优势。

4 基于错误保护的几何图像压缩编码

本节主要讨论基于错误保护的几何图像压缩编码方法。与普通的图像数据相比，本文方法的创建几何图像数据具有以下特点

1)几何图像呈现为边界清晰的数片；背景部分对应未定义的点，值均为(0,0,0)；

2)每片图像数据对应于三维模型上某一片模型表面几何信息的规则采样，片内数据相关性很强，有较大的空间冗余，即在相邻像素间、相邻行间存在着强相关性；

为了去除大部分的背景区域，本文采用了简单的数据分块策略：将图像分割成8×8的小块，按照从左到右，从上到下的顺序记录每小块的序号，对于只包含背景，即值均为(0,0,0)的图像，无需做进一步处理。这些区域在全部数据解码之后，直接填入(0,0,0)值即可。如图4所示。

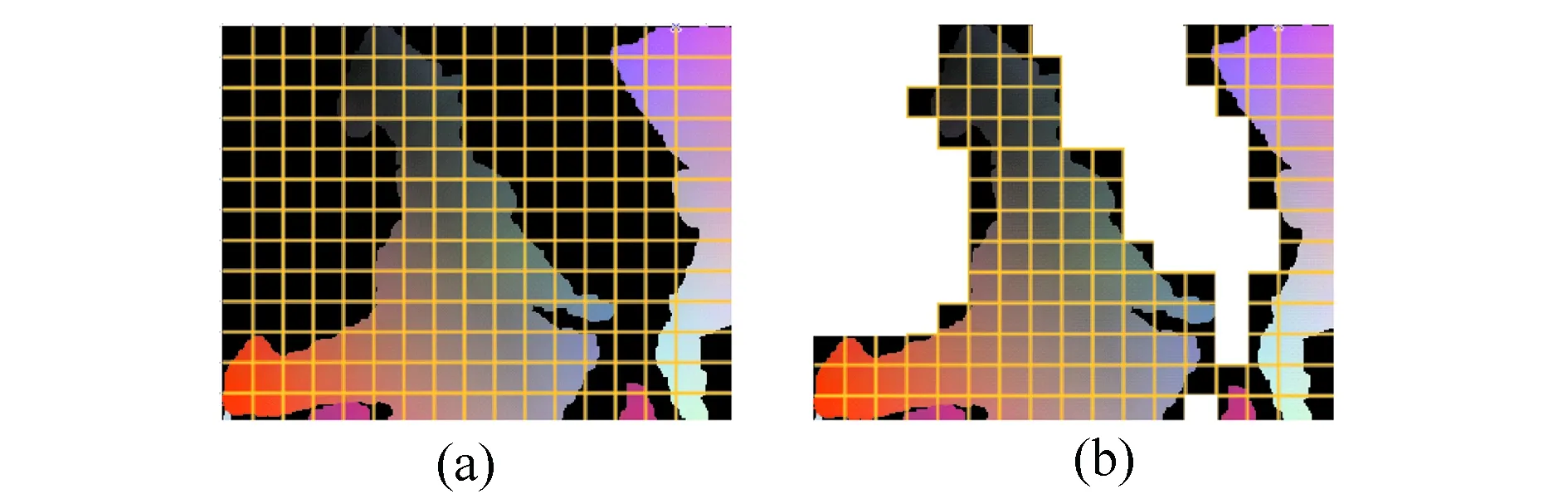
图4 (a)图像分块 (b)背景剔除

要消除相邻像素间、相邻行间存在的强相关性，必须采用变换编码，通过将图像能量在空间域的分散分布变为在变换域的相对集中分布，获得对图像信息的有效压缩。

常用的变换编码有K-L变换编码，离散余弦变换(DCT)编码和小波变换编码。K-L变换编码理论上可以得到最优的压缩比，但其运算量过大。离散余弦变换(DCT)编码最接近最佳K-L变换，相关理论成熟，有快速算法，且适用于图像的分块压缩。采用这种方法，对于几何图像这种空间冗余较大的数据，可以达到良好的去相关性和能量集中效果，如图5所示。

图5 (a)输入的8×8图像块矩阵(b)DCT变换得输出矩阵

由以上变换的结果可知：0行0列具有的DCT系数比其它DCT系数大得多，它称作直流(DC)系数。其余系数称为交流(AC)系数。AC系数的值随着它与DC系数的距离增加而越来越小。在作一般图像有损压缩时，仅保留直流系数和左上角的交流系数就能够保留大部分的图像信息，从而达到大幅度压缩图像的目的。为了确保压缩舍入误差得到较好控制，不影响后续三维重构，本文对交流系数采取了如下近无损量化方法

(4)

经过DCT变换和近无损量化后，每个图像块需编码的信息如下：图像块的序号、直流系数和交流系数。有于图像块的序号非常重要，同时误码弹性 图像编码要求直流系数不应相互依赖。由此，一种定长编码(FLC)就被用于编码块序号和直流系数，对交流系数，就采用霍夫曼(Huffman)编码。这样每个图像数据块由定长编码的块序号和霍夫曼编码的交流系数组成，块与块之间插入可选择的重置标志码(RSTm标志码)，将传输误差控制在块边界内。

整个基于错误保护 的几何图像数据的压缩编码过程如图6所示。

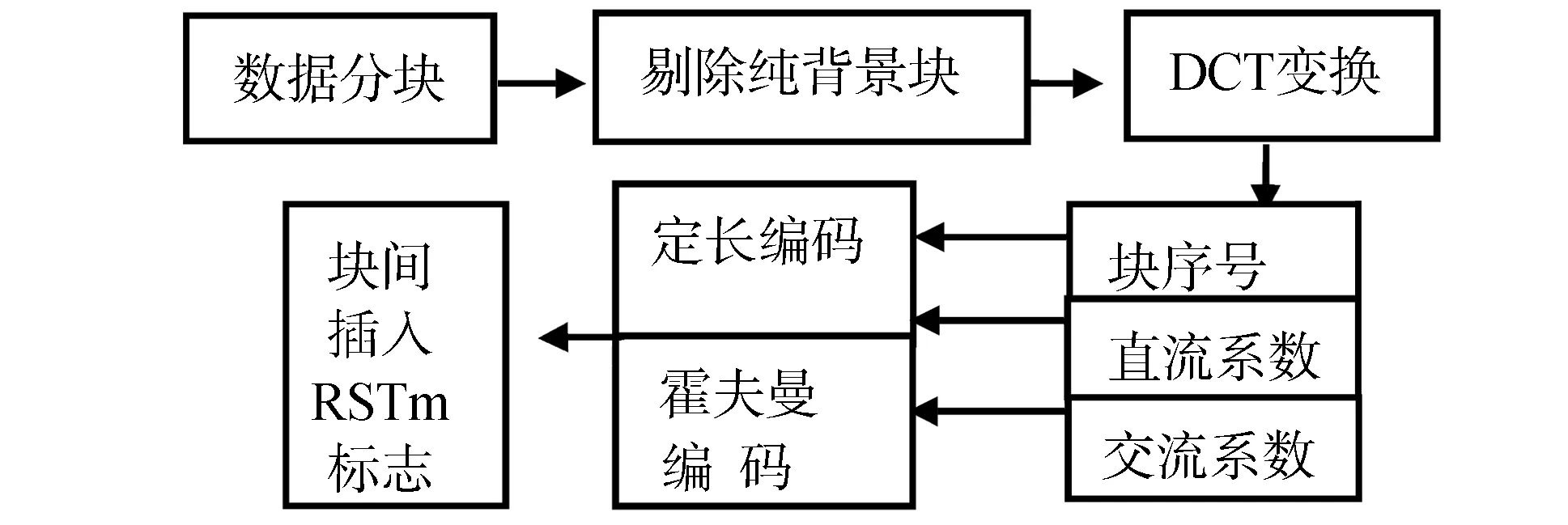
图6 基于错误保护的几何图像压缩流程

通过去除背景数据块，以及对图像做分块DCT变换，近无损量化，并对交流系数霍夫曼编码，几何图像数据的大部分冗余被去除，实验数据表明压缩比可达3.8～9.4之间；同时数据分块，对块序号、直流系数定长编码，并在块之间加入RSTm标志等措施，使几何图像数据得到了有效的错误保护。

5 试验结果与分析

为了得到本文所述的编码方法在误码弹性和编码效率方面的具体表现，我们选择了不同亏格、不同复杂程度的模型，进行了大量的实验。

实验结果验证了本文方法的广泛适用性：对于高亏格或有较长突起的模型，根据几何图像重构的模型仍能较好的保持初始模型特征，如图7所示。

将本文所述的几何图像压缩编码方法应用于不同数据规模的模型，所得到的结果表明：相对于三角网格数据，几何图像数据所需的存储空间均比三角网格数据小，且具有更好的可压缩性能。具体数据如表2所示。

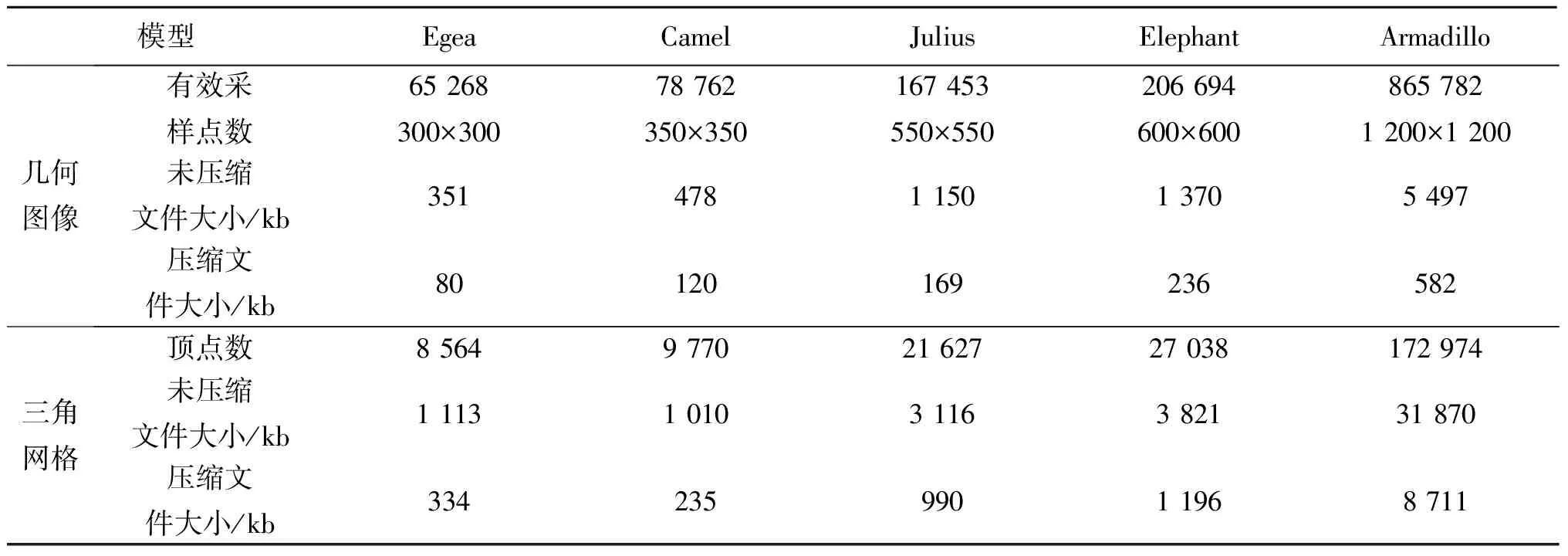
表2 几何图像与三角网格所需的存储空间对比

图7 (a)初始模型；(b)几何图像；(c)重构模型

为了得到本文方法在误码弹性方面的具体表现，本文以五组三维模型作为测试数据，分别采用的几何图像和传统的三角网格进行编码，各进行了500次模拟传输实验。传输速率约为256 kbits/s，分别以10-2、10-3、10-4、10-5随机产生的脉冲信号作为加性噪声表示不同的随机误码率。

所得具体实验数据如表3所示(其中GI为几何图像，GI_C为采用本文方法压缩的几何图像，TM为三角网格，TM_C为rar压缩的三维网格)。

表3 三维模型在不同随机BERs下的传输正确率

6 结 论

为了解决普适计算环境下传输信道误码率较高，同时三角网格模型不规则的网状结构对于传输错误又非常敏感的矛盾，本文提出了一种基于几何图像的三维模型错误保护编码方法。

采用本文提出的均匀准保角平面参数化方法对模型做低误差的参数化处理，三维模型的几何信息可被均匀的采样，并进一步编码为二维图像的方式。随着其不规则的网状结构消除，模型数据之间关联性大大降低，同时相关性增强。因此这种编码的三维模型数据，其误码弹性可得到根本改善。

为了节省普适计算环境下的网络带宽资源，进一步提高编码效率，本文还给出了基于错误保护的压缩编码方案，取得了编码效率和误码弹性之间的较好平衡。模拟试验的结果表明，与常规的三角网格编码方法相比，这种编码方法从根本上改善了三维模型数据的误码弹性，并只需较少的存储空间。

这种编码方法的主要不足如下：在构造三维网格模型的规则采样数据时，目前采用的参数化方法虽可确保参数化误差较小且可控，但造成三维模型切割路径较长，导致以下两个问题：①在传输终端，根据规则采样数据重构三维模型时，模型片缝合步骤计算复杂且耗时较多；②在构造三维网格模型的规则采样数据时，当采样密度较低时，会造成重构模型上明显的缝合痕迹和变形。

因此下一步的研究工作应包括两方面：一方面要研究新的平面参数化方法，在确保参数化误差较小的同时尽量减少切割路径，致力于解决上述问题；另一方面应借鉴图像与视频最新的错误保护和压缩编码方法，对三维网格模型的规则采样数据进行更高效的基于错误保护的压缩编码。

参考文献：

[1]HAN Y H, LEOU J J.Detection and correction of transmission errors in JPEG images [J].IEEE Transactions on Circuits and Systems for Video Technology, 1998, 8(2): 221-231.

[2]赵慧民,方艳梅.率失真最优自适应量化及其系数阁值的设定[J].中山大学学报：自然科学版, 2004, 43 (3) : 32-35.

[3]赵慧民, 方艳梅.一种非均匀错误保护实现最优码率分配的技术[J].中山大学学报：自然科学版, 2007, 46(1): 43-47.

[4]ZHANG Q, LIU G.Error resilient coding of H.264 using intact long-term reference frames [C]∥Visual Information Engineering, 2008: 62-66.

[5]AL-REGIB G, ALTUNBASAK Y, ROSSIGNAC J.A joint source and channel coding approach for progressively compressed 3-D mesh transmission [C]∥ICIP, 2002: 161-164.

[6]HAN M J, SONG M S, KIM S J, et al.Results of M5 code-experiments [C]∥ISO/IEC JTC1/SC29/WG11, MPEG98/M4516, 1999.

[7]PARK S B, KIM C S, LEE S U.Error resilient 3-D mesh compression [J].IEEE Transactions on Multimedia, 2006, 8(5): 885-895.

[8]YAN Z D, KUMAR S, KUO C C J.Error-resilient coding of 3-D graphic models via adaptive mesh segmentation [J].IEEE Transactions on Circuits and Systems for Video Technology, 2001, 11(7): 860-873.

[9]YAN Z D, KUMAR S, LI J, et al.Error resilient coding of 3D graphics based on morphing and volume splitting [C]∥SPIE Int Symp Voice, Video and Data Communications, Boston, MA, 1999: 128-136.

[10]YAN Z D.Efficient and robust compression on 2D and 3D graphics [D].Los Angeles: Univ of Southern California, CA, 1999.

[11]YAN Z D, KUMAR S, LI J, et al.Reversible variable length codes (RVLC) for robust coding of 3D topological mesh data [C]∥Proc Data Compression Conference ’99, 1999: 560-566.

[12]GU X, GORTLER S, HOOPE H.Geometry images [C]∥ACM SIGGRAPH 2002, 355-361.

[13]SANDER P, WOOD Z, GORTLER S, et al.Multi-chart geometry images [C]∥Eurographics Symposium on Geometry Processing, 2003:146-152.