高职院校毕业生社会适应能力评价指标体系构建研究

罗 艳

（南华工商学院，广东 广州 510507）

一、高职院校毕业生社会适应能力概述

社会适应能力是一种综合能力。关于其具体包括一些什么能力，至今仍没有定论。根据高职院校毕业生自身特点，综合现有研究成果，本文采用多种方法，对社会适应能力的构成要素进行分析，包括（1）文献资料法：运用现代教育理论和方法，结合哲学、管理学及其他理论基础，对高职院校结合社会实际进行教育改革的理论进行探索，筛选高职毕业生所应具备的社会适应能力特征。（2）专家咨询法：通过向多位高职院校的教授及毕业生就业工作专家就高职毕业生社会适应能力指标进行咨询，对高职毕业生社会适应能力所包含的因素整理归类，在意见相对一致情况下，统一从四个大的方面，共包括十三种要素作为衡量其社会适应能力的标准。（3）层次分析法及Matlab软件的应用：运用层次分析的理论和方法建立社会适应能力指标评价模型，对不同层次要素通过分析比较量化处理，利用Matlab软件对相应的矩阵进行计算，从而确定各要素对社会适应能力的影响权重。

二、利用APH方法构建高职院校人才适应性指标评价体系

1.层次分析法概述

层次分析方法（AHP）是美国运筹学家T.L.Saaty教授于20世纪70年代创立的定性与定量相结合的决策方法，它能够将复杂的决策过程系统化、数量化和模型化，并通过递阶层次模型建立、两两对比判断矩阵构建、层次单排序、层次总排序和一致性检验等环节，确定复杂决策中各种因素之间的重要程度（即权重），并加以排序。

2.建立层次结构图

基于对影响高职院校毕业生社会适应能力评价因素的分析，可运用层次分析法建立层次模型，设高职院校毕业生社会适应能力评价为目标层A层，准则层为B层，包括基本工作能力，职业工作能力，适应潜力，素质素养，分别设为B1、B2、B3、B4，在B层下面再设立C层，即C1-C13，如图1所示。

图1 高职院校毕业生社会适应能力评价指标体系

3.构造比较矩阵

（1）完成层次模型后，将各层因素对上一层因素的相对重要性进行两两比较，请有关专家给出判断矩阵的元素值，从而得到层次分析的判断矩阵。假定A层元素与B层元素B1，B2，…，Bn有联系，则构造的判断矩阵如表1所示：

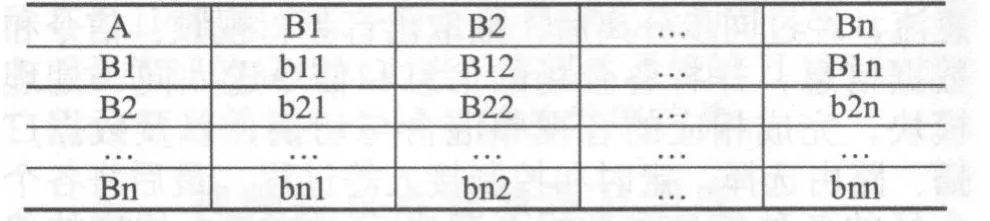
表1 判断矩阵构建

其中bij表示对于A而言，Bi对Bj的相对重要性，通常bij取1，2，…，9及它们的倒数，其含义见表2。

表2 比例标度值及其含义

显然，对判断矩阵有：bii=1，bij=1/bji（i，j=1，2，…，n），因此，对于n阶判断矩阵，我们仅需要对n（n-1）/2个元素给出数值。

（2）相对权重向量确定。层次分析法一般与德尔菲法结合起来运用，经专家及评价小组相关人员讨论各因素的重要性，则可得各层次比较矩阵。本文以ABi判断矩阵（见表3）为例说明其求解过程，具体如下：

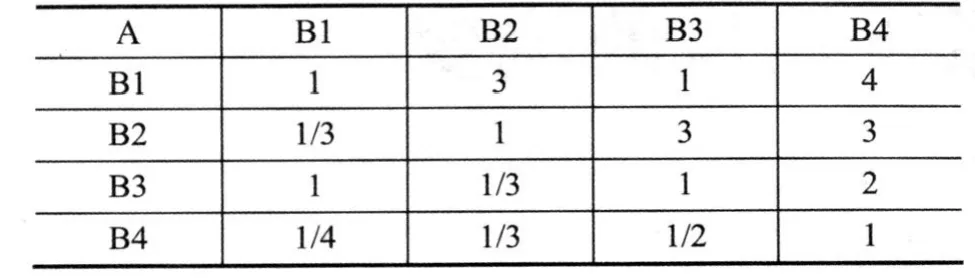
表3 A至Bi判断矩阵

使用Matlab6.5软件，在其命令框内依次输入命令：B=［1，3，1，4；0.333，1，3，3；1，0.333，1，2；0.25，0.333，0.5，1］，［x，d］=eig（B），wa=x（：，1）/sum（x（：，1）），由此即可得出λmax1＝4.4345，相应特征向量ω1＝（0.7515，0.5280，0.3624，0.1587），特征向量ω归一化后为Wa1=（0.4174，0.2932，0.2013，0.0881）。相应地，可利用Matlab软件求出第三层C层各对应的特征值及特征相量和将特征向量归一化后的值。见表4。

表4 B1，B2，B3，B4分别对应C层的特征值及特征相量和将特征向量归一化后的值

4.单排序的一致性检验

AHP法的主要优点是将决策者的定性思维过程定量化，但由于评价对象是个复杂的系统，不同的专家在认识问题上存在不可避免的多样性或片面性，即使有九级标度也不一定都能保证每个判断矩阵具有完全一致性，因此必须通过一致性检验检查各个指标的权重之间是否存在矛盾之处。基于矩阵基础理论的一致性检验步骤如下：

首先，计算判断矩阵的最大特征值（或称最大特征根）λmax；其次，计算一致性指标CI：CI＝（λmaxn）/（n－1）。式中，n为判断矩阵的行数，也即层次子系统中的指标个数。最后，计算随机一致性比率CR：CR＝CI/RI。其中，RI为随机一致性指标（见表5）。

表5 平均随机一致性指标值

依据Matlab软件计算所得高职院校毕业生社会适应能力指标的相关数据，求得相应的CI和CR值。

表6 CI和CR值

当CR≤0.10时，判断矩阵具有满意的一致性，CR＜1时被认为一致性可以接受。否则，应对判断矩阵予以调整。如上述3例判断矩阵，可计算得CR全部小于1，因此，判断矩阵符合一致性要求，层次单排序结果有效可靠。

最后，根据求特征根和特征向量方法，分别求出各因素的相应权重，然后求出它们的合成权重（Bi×Ci）。最后进行各因素权重的总排序（见表7）。这样使各层次、各个要素在社会适应能力上的影响程度就显而易见了。

表7 合成权重层次总排序

5.结果与分析

通过对社会适应能力诸因素进行层次分析，可清楚看到，在适应性能力中占主要成分的是毕业生的基本工作能力，然后依次是职业工作能力、适应性潜力及素质素养。再从合成权重的排序中看到，在13种因素中，沟通交流能力及专业知识掌握等的权重值较大，基实质也即如何处理好人际关系的问题，说明了处理好人际关系的重要性。

从以上计算结果的分析可以看到，所选择的社会适应能力因素是准确的，分析计算的方法也是可行的，对各类因素权重顺序也较符合社会实际。通过对高职毕业生所应具备的社会适应能力的了解，为学校制定相应的人才培养模式和完善培养措施提供依据。

三、结 语

社会适应能力是一种社会实践能力。培养高职院校毕业生具备社会适应能力是现代社会的需要，也是教育改革、为社会培养应用型人才的方向。由于我国高职院校在人才培养方面缺乏经验，培养人才模式需进一步完善，通过对社会适应性能力的量化分析，从社会适应角度反视学校培养，促进高职院校发展。同时，社会适应能力是人的心理、知识、才能等方面有维度、有层次的综合体现。各种特征相互联系、相互促进，是不可分割的整体。但其影响程度是不同的，在对学生培养过程中应有所区别。利用层次分析的方法对社会适应能力的指标进行了量化处理，并对影响程度赋于了不同权重，排出适应能力中各要素的作用顺序，为高职院校的人才培养规划提供参考依据。

［1］王学臣，牛庆忠.大学毕业生社会适应状况调查［J］.健康心理学杂志，2001，（4）：271-272.

［2］张喜爱.高校科研团队绩效评价指标体系的构建研究——基于AHP法［J］.科技管理研究，2009，（2）：226-227.

［3］张茂玻.略论我国高职院校学生社会适应能力的培养——基于对四川高职院校学生社会适应能力的调研［D］.西南财经大学，2009.

［4］胡运权，郭耀煌.运筹学教程［M］.北京：清华大学出版社，2003.