球笼式万向节接触应力的计算及球组节圆直径的优化设计
2011-07-23石宝枢
石宝枢
(比亚迪汽车有限公司 传动轴总厂,广东 深圳 518118)
符号说明
a——2个钢球接触面的半径,mm
DK——钟形壳最大外径,mm
Dpw——球组节圆直径,mm
Dw——钢球直径,mm
DZ——传动轴公称直径,mm
E——材料的弹性模量,GPa
K——球组节圆直径系数
P——2个球承受的压力,N
R1,R2——圆球半径,mm
RK——钟形壳沟道底部半径,mm
RX——星形套沟道底部半径,mm
δ——2个接触球中心变化量,mm
σmax——接触应力的最大值,MPa
μ——材料的泊松比
球组节圆直径是球笼式万向节至关重要的结构主参数,其值直接关系到:(1)星形套与钟形壳沟道直径的大小;(2)偏心距、球面径等其他主参数是否合理;(3)保持架结构主参数如何优化设计;(4)在已知的、有限的空间内,如何进行几何结构布置,以达到科学、合理及最佳的尺寸匹配;(5)产品的承载能力和使用寿命。但目前国内、外几乎所有的企业在球笼式万向节设计中并没有对该值进行系统的、精确的优化,导致钟形壳、星形套、保持架受力极不平衡,处于薄弱环节的星形套和保持架出现过早失效的现象非常普遍。使国内、外售后市场出现了单独更换星形套和保持架,而钟形壳无任何损坏的不正常、不合理现象。
下文通过对球笼式万向节零件间Hertz接触的应力分析和球组节圆直径的优化设计,以期系统地解决上述问题。
1 钢球与星形套和钟形壳的Hertz接触
如图1所示,球笼式万向节主要由星形套、钟形壳、保持架和钢球等组成,以传递两相交轴在一定角位移范围内的运动和转矩。
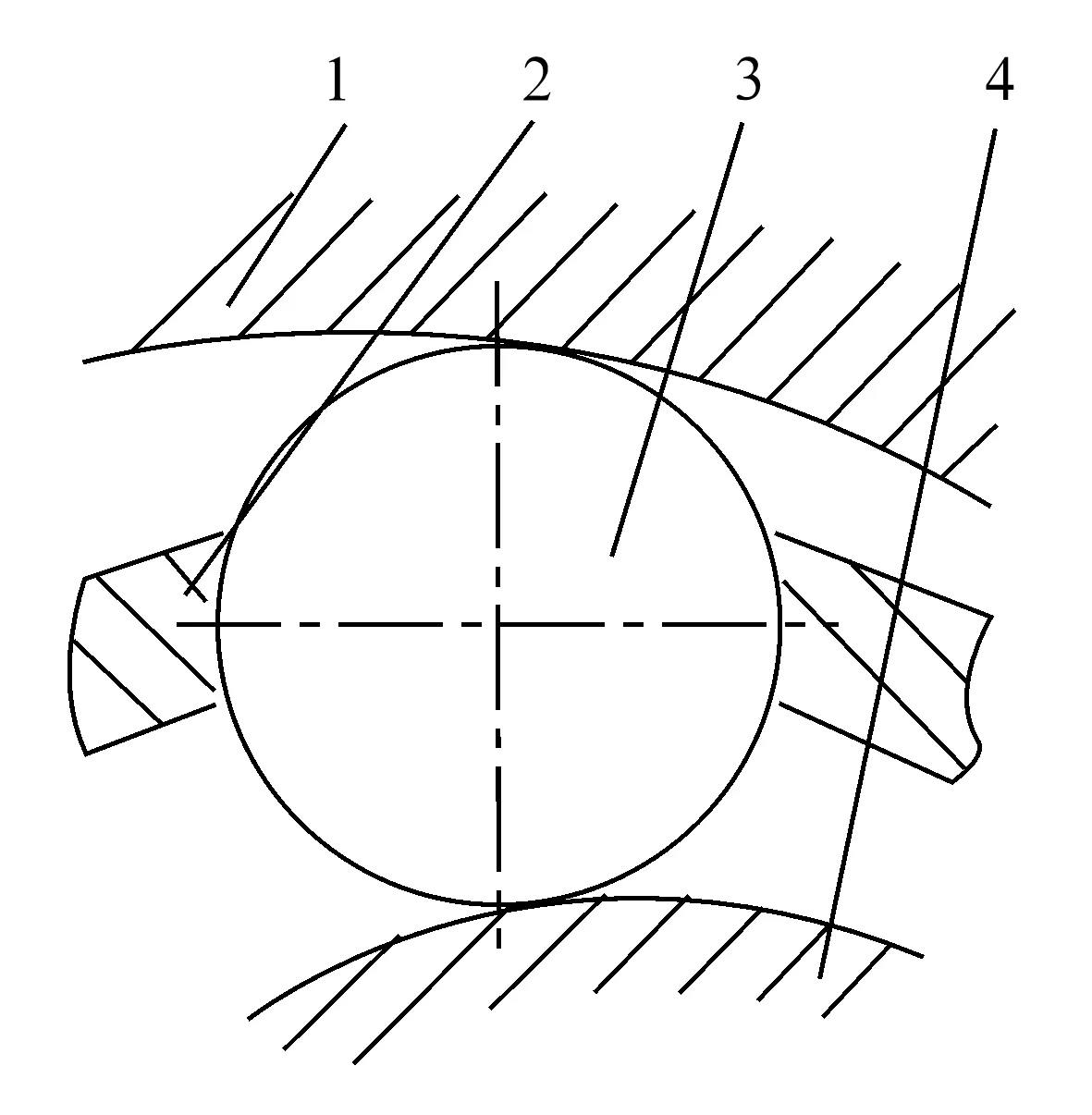
1—钟形壳;2—保持架;3—钢球;4—星形套图1 球笼式万向节的结构
在恒定转矩或交变等复杂转矩的作用下,2个钢球基本上不旋转,在各自的沟道内缓慢滚动。工作时,星形套和钟形壳在圆周上无相对转动,只通过2个钢球的滚动和保持架的引导而缓慢地摆动,基本属于静态运转工况。在该工况下,钢球与星形套及钟形壳之间均为共轭Hertz接触,显然,星形套、钟形壳和钢球主要承受接触应力。它们主要的失效模式是接触疲劳破坏,因此应按Hertz接触理论进行分析,计算其承载能力,校核其接触疲劳强度,并进行相应几何尺寸的优化设计,以达到对球笼式万向节精确、合理的设计。
2 接触应力的分析与计算
2.1 2个圆球的接触分析
如图2所示,设2个圆球的半径分别为R1和R2,2个圆在公切平面上O点相互接触。此时在2个球的截面上与轴Z1和Z2有微小距离r的2个点M,N的坐标Z1和Z2可分别近似地表示为

图2 2个圆球的Hertz接触
(1)
(2)
显然,M和N2个点的距离为
(3)
当2个球体受力P的作用沿着O点的法向互相压紧时,在接触点处发生局部变形,而形成1个微小的圆接触面,由于R1和R2远远大于接触面的半径,可将球看作是半空间。设ω1为球体1面上点M由于局部变形所产生的沿Z1轴方向的向下位移;ω2为球体2面上的点N由于局部变形所产生的沿Z2轴方向的向上位移。设2个球中心距O1O2的变化量为δ。如果由于局部变形使M和N点落到接触面的内部,则
δ=Z1+Z2+ω1+ω2。
(4)
由于对称性,由压力P产生的压应力σ和位移ω对于接触面中心O均为中心轴对称,接触应力可按半球形分布进行求解。根据变形连续条件和静力平衡,可求得2个圆球接触面半径为[1]
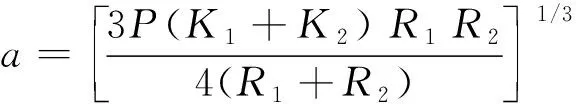
(5)
2个圆球中心距的变化量为[2]

(6)
接触面中心O处的最大压应力为
(7)
由以上公式可知,最大接触应力与载荷不是线性的关系,而是与载荷的立方根成正比。这是因为随着载荷的增加,接触面积在增大,其结果使接触面上的最大压应力的增长慢于载荷的增长。
2.2 钢球与星形套接触应力的计算
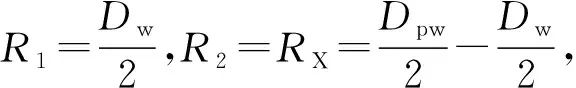
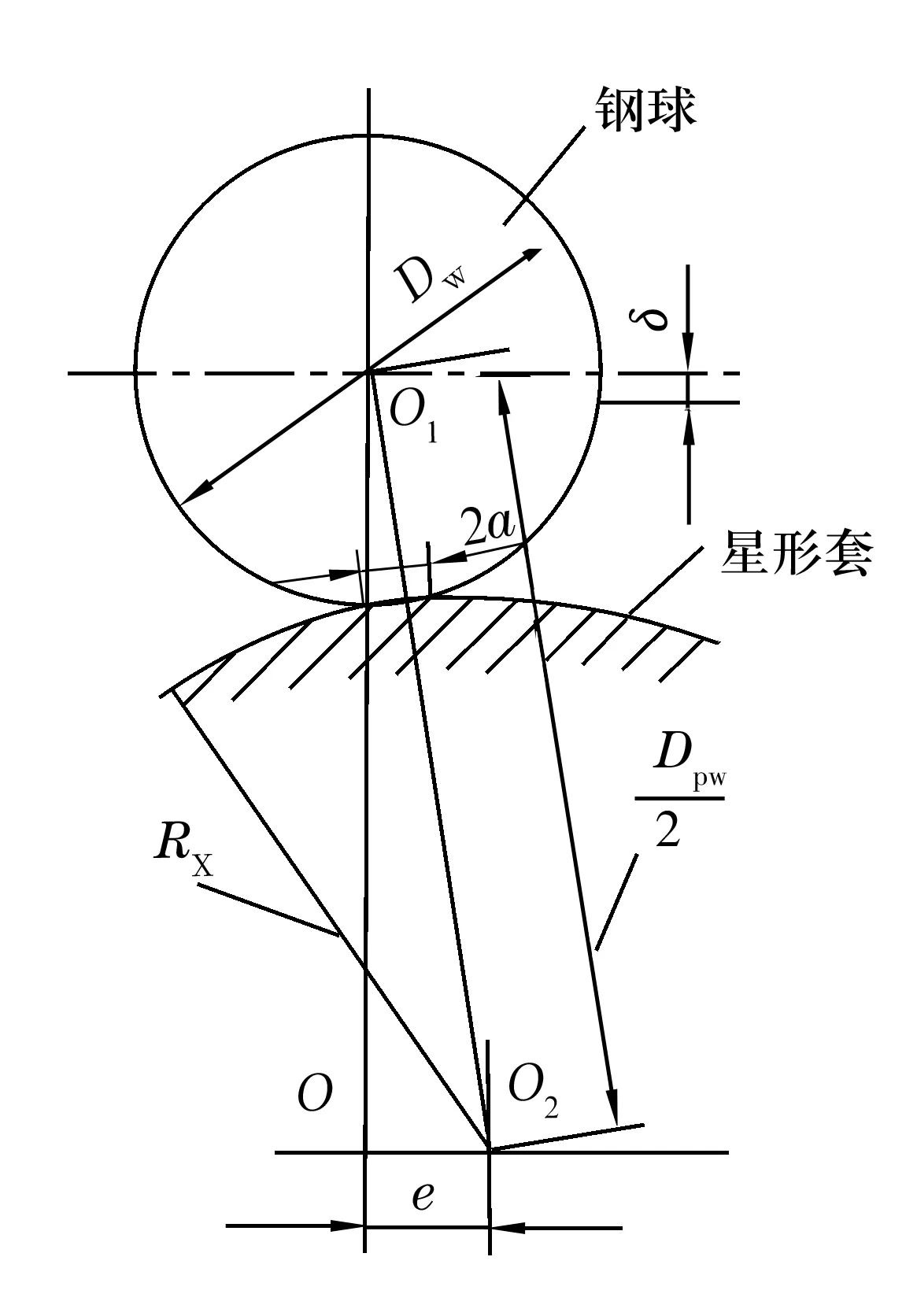
图3 钢球与星形套的接触
(8)
钢球与星形套中心距的变化量为
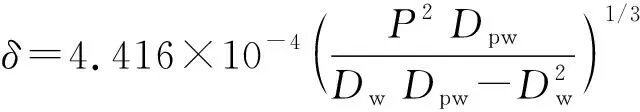
(9)
钢球与星形套接触应力的最大值为
(10)
2.3 钢球与钟形壳接触应力的计算
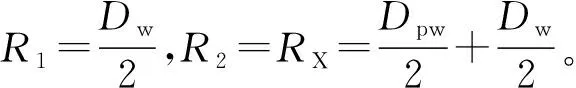
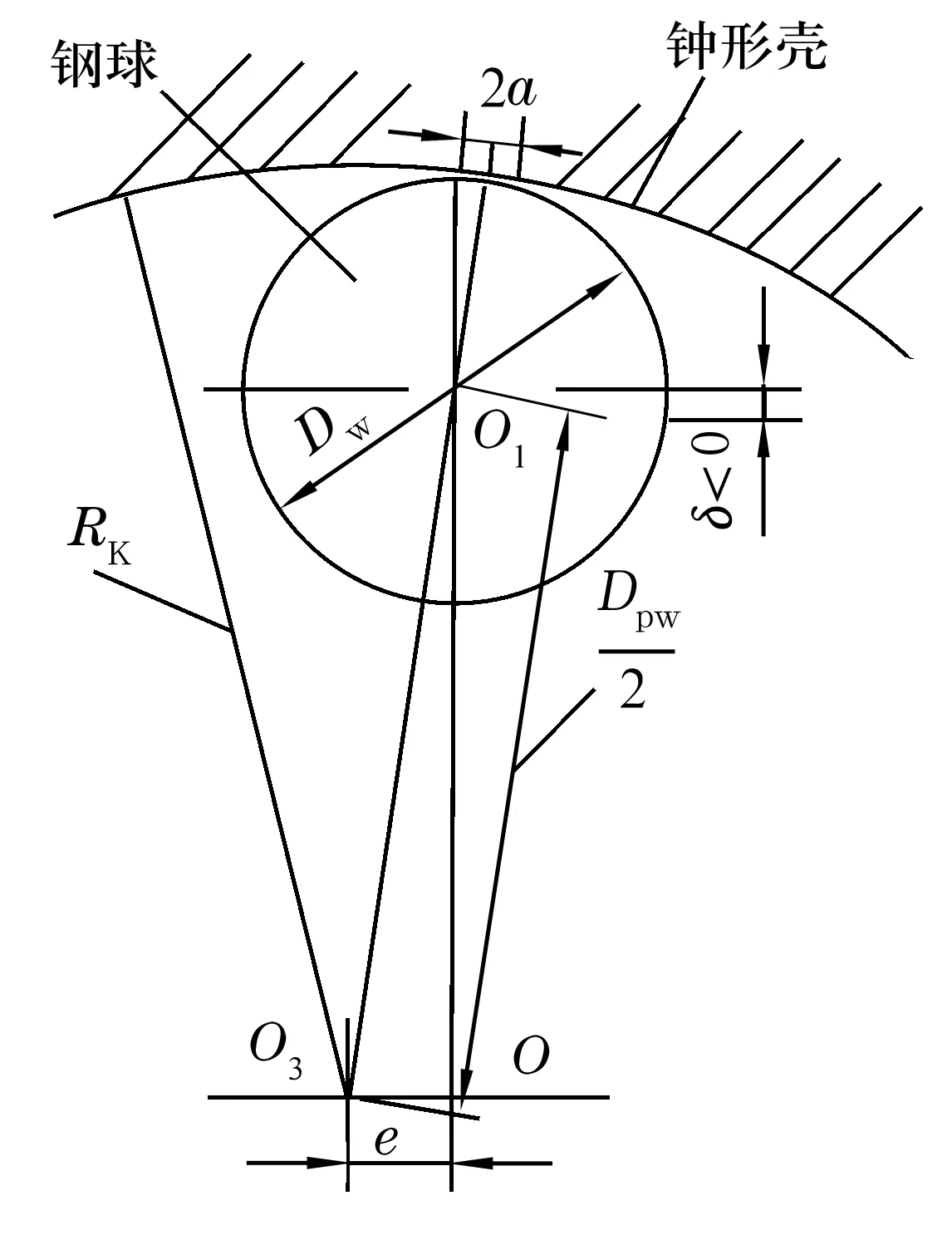
图4 钢球与钟形壳的接触
(11)
钢球与钟形壳中心距的变化量为
(12)
钢球与钟形壳接触应力的最大值为
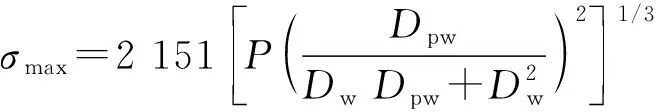
(13)
当然,最理想状况是在同时受作用力P时,星形套和钟形壳的应力相等,由(10)和(13)式,则有
解得Dw=0。
由此可知,只有当无钢球时,两者的接触应力相等,这种情况是不存在的。或者说,只要有钢球,在0 球笼式万向节球组节圆直径的大小,取决于钢球的空间位置。换言之,研究的目的是在已知的、有限的空间范围内对钢球进行布置,使星形套与钟形壳实现最佳的壁厚比,使两者实现最科学、最合理及最佳的应力匹配,以最大限度地提高整个球笼式万向节的承载能力,并延长其使用寿命。 球笼式万向节的有效壁厚为0.5(DK-DZ),壁厚中心圆直径为0.5(DK+DZ)。现引入球组节圆直径系数K的概念,则球组节圆直径Dpw的一般式为 Dpw=K(DK+DZ)。 (14) 钟形壳和传动轴的外径一般为 DK=5Dw[3], (15) DZ=1.4Dw。 (16) 由(14)~(16)式得 Dpw=6.4KDw。 (17) 现讨论3种情况下星形套与钟形壳的应力差。 (1)K=0.5。此时,球组节圆直径等于壁厚中心径,即Dpw=3.2Dw,将其分别代入(10)和(13)式,可得星形套和钟形壳最大应力分别为 两者应力差为53.9%。 (2)K=0.45。此时,球组节圆直径小于壁厚中心径,即Dpw=2.88Dw,将其分别代入(10)和(13)式,可得星形套和钟形壳的最大应力分别为 两者应力差为62.11%。 (3)K=0.55。此时,球组节圆直径大于壁厚中心径,即Dpw=3.52Dw,将其分别代入(10)和(13)式,可得星形套和钟形壳的最大应力分别为 两者应力差为47.61%。 由上述计算可知,无论Dpw或K取何值,星形套最大接触应力始终大于钟形壳的最大接触应力。上述3种情况,只有当球组节圆直径大于壁厚中心直径时,星形套和钟形壳的应力差最小。所以产品设计时,应在满足钟形壳有效壁厚的前提下,最大限度地提高K值。 解得K=0.547,取K=0.54~0.55 。 (1)球笼式万向节的钢球与星形套和钟形壳间的最大接触应力与载荷的立方根成正比。 (2)星形套最大接触应力始终大于钟形壳最大接触应力。产品设计时,应力求避免两者应力差过大,最大限度地使两者实现最佳的接近。 (3)球笼式万向节球组节圆直径系数K=0.54~0.55是优化设计的最佳结果。3 球组节圆直径的优化设计
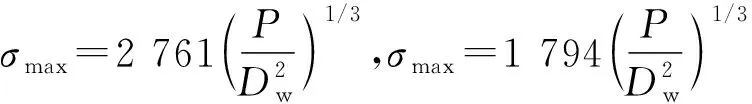
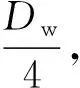
4 结论
