基于数理统计理论的中国轴承产业专利趋势预测

牛青波，贾现召，叶军

(1. 河南科技大学 机电工程学院，河南 洛阳 471003；2.洛阳轴研科技股份有限公司，河南 洛阳 471039；3.河南省机械设计及传动系统重点实验室，河南 洛阳 471003)

随着知识产权主体地位的不断提升，国内、外企业也都把专利作为市场竞争的另一利器，专利预测则成为企业或政府制定专利战略规划和决策时考虑的必要因素。对专利文献数据进行统计只能了解在过去一段时间内的专利申请和研发趋势情况，而通过对已知的专利文献数据进行统计则能够对未来该企业或地区相关专利情况做出预测，有效帮助企业或政府制定相应的战略决策。但由于专利申请数据的变化受国家政策、企业技术投入、企业管理模式改变及技术人员数量等多种因素影响，无法判断影响专利申请数据的主要因素，统计理论中无法使用回归预测分析方法。下文采用专利信息定量分析方法中的时间序列分析预测以及灰色系统分析预测方法，预测国家或竞争对手专利申请数量的发展趋势。

1 专利统计数据预处理

通过中国知识产权网专利数据库[1]对1985年4月1日—2010年12月31日间公开的专利申请进行检索，检索名称定义为“轴承 or 保持架 or 保持器 or 滚动体”，摘要定义为“轴承”，或者检索式定义为“摘要=(轴承) and 名称=(轴承 or 保持架 or 保持器 or 滚动体)”。由于中国《专利法》规定，发明专利申请一般自申请日起满18个月才公告，因此2010年的专利申请公开有滞后，目前公开的专利数据不能完全反映2010年度的专利申请情况。为此利用专利管理图仅对1985年4月1日—2008年12月31日的专利申请进行趋势研究，并对2009年和2010年中国轴承产业技术领域的中国专利申请趋势、国外在华申请趋势及国内专利申请趋势进行预测。

对于专利统计数据，充分考虑样本的代表性，使其能够有效反映专利申请数据的变化规律，采用研究对象的总和作为数据样本，统计数据见表1～表3。以下的分析计算中均以当年专利数量作为统计分析的原始序列数据。

表1 2002—2008年中国轴承技术领域专利申请统计表

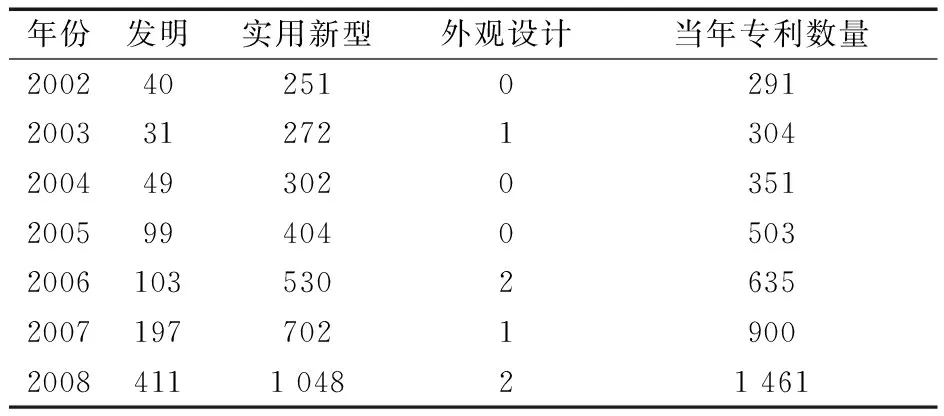
表2 2002—2008年国内专利申请人轴承技术领域专利申请统计表

表3 2002—2008年国外专利申请人轴承技术领域专利申请统计表

2 基于Logistic生长曲线和灰色动态模型的预测

时间序列分析预测是将预测目标的统计数据按照时间顺序排列成为时间序列，分析其随时间的变化趋势，预测目标的未来值。生长曲线预测方法是技术预测中的一种常用方法，特别是Logistic曲线，其对于大多数产业统计时系列数据具有高度的适用性[2]。由于专利件数申请量成因复杂，各年度专利申请具有多变性，采用灰色系统理论进行专利趋势预测，可以剔除不可比因素，并且对预测所需的专利数据多少不限，建立的数学模型能够满足精度要求，预测结果更加可靠。

2.1 Logistic曲线计算

2.1.1 三等分计算方法

设时序列数据为y，t表示时序列号，则曲线公式

Y=k-ABt，

(1)

(2)

(3)

(4)

(5)

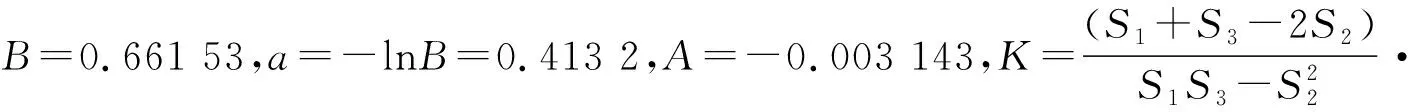
n=4 407.243，m=-A·K=13.851 96，则

(6)

2.1.2 利用SPSS拟合Logistic曲线方程

根据上述三等分计算方法测算估计K=4 400，运用社会科学统计软件(Statistical Package for the Social Sciences，SPSS)[3]模拟原始序列数据y曲线，得

(7)

从软件计算可知R2=0.981，其中R2是以回归偏差占总偏差的比率来表示回归模型拟合优度的评价指标，该处R2值表明模型对数据的拟合度非常好(以下均采用SPSS拟合的Logistic曲线进行预测)。中国轴承产业技术领域预测的专利申请见表4，表中数据均取整。原始序列数据y的Logistic回归曲线如图1所示。

图1 中国轴承产业技术领域年度专利申请总量Logistic预测曲线

表4 中国轴承技术领域专利申请逻辑曲线计算预测表

同理，国内轴承企业技术领域年度专利申请预测Logistic曲线方程为

(8)

软件计算得R2=0.963，表明模型对数据的拟合度较好。预测数据见表5，Logistic回归曲线如图2所示。

表5 国内专利申请人轴承技术领域专利申请逻辑曲线计算预测表

图2 国内企业轴承技术领域专利申请Logistic预测曲线

同上，国外轴承企业在华技术领域专利申请预测Logistic曲线方程为

(9)

软件计算得R2=0.975，表明模型对数据的拟合度较好。预测数据见表6，Logistic回归曲线如图3所示。

表6 国外专利申请人轴承技术领域专利申请逻辑曲线计算预测表

图3 国外企业轴承技术领域专利申请Logistic预测曲线

2.2 灰色动态预测法模型构建

在专利技术趋势预测中，采用灰色预测模型中的GM(1，1)模型。GM(1，1)模型是基于随机的原始时间序列，经按照时间累加后形成新的时间序列所表现出的规律，其近似满足微分方程条件。

设原始时间数据列X(0)={X(0)(1),X(0)(2),…,X(0)(n)}，

(10)

对原始序列进行一次累加后，得到的新数据列

X(1)={X(1)(1),X(1)(2),…,X(1)(n)}

。(11)

则GM(1，1)模型相应的微分方程为

(12)

式中：α为发展灰数；μ为内生控制灰数。

(13)

(14)

根据(10)～(14)式和表1的数据(选取2003—2008年的数据)可得：

X(0)=(365，436，650，833，1 148，1 716)，

X(1)(365，801，1 451，2 284，3 432，5 148)，

Y=(436，650，833，1 148，1 716)。

表7 中国轴承技术领域专利申请逻辑曲线计算预测表

同理，利用灰色动态预测模型计算得到国内企业轴承技术领域专利申请预测趋势见表8，国外企业轴承技术领域专利申请预测趋势见表9。

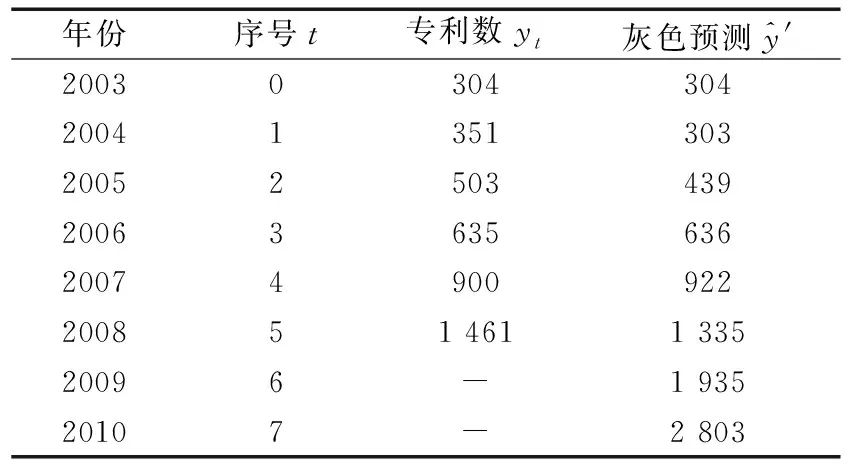
表8 国内专利申请人轴承技术领域专利申请灰色预测表

表9 国外专利申请人轴承技术领域专利申请灰色预测表

3 模型预测精度评价

根据上述计算得出的预测值，利用预测精度评价函数对以上2种数学模型进行精度评价(均以中国轴承技术领域预测结果为例)。

3.1 生长曲线Logistic数学模型

则有

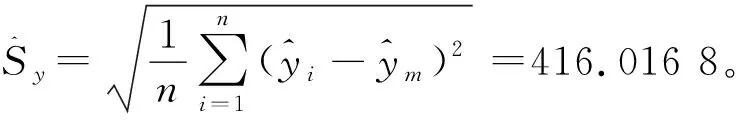
3.2 灰色动态GM(1，1)数学模型

则有

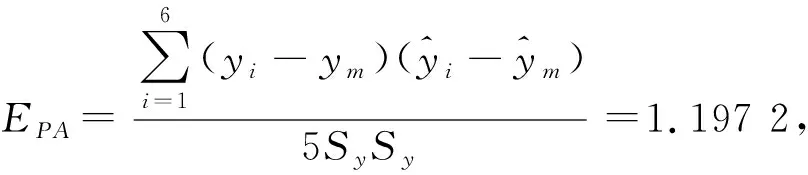
3.3 灰色模型检验

灰色动态模型使用方差比和常用的小误差概率对模型进行检验。预测误差

(15)

故有e(1)=0；e(2)=13；e(3)=57；e(4)=2；e(5)=17；e(6)=83。

GM(1，1)模型精度等级见表10,精度等级越小越好，4级为不通过。由表可知，文中取得的模型精度符合1级，说明预测结果可靠性较高，即灰色动态预测模型的预测结果更为准确可靠。

表10 灰色动态GM(1，1)模型精度等级表

4 结束语

利用数学统计理论对中国轴承产业专利信息进行定量分析，通过时间序列生长曲线以及灰色动态数学模型的建立，对比计算分析了2种统计预测理论的精度，同时对灰色动态模型的可靠性进行了评价，进而有效预测了中国轴承产业未来2年的专利技术申请趋势。结合以上2种预测方法，可以得出中国轴承技术领域2009年专利申请约为2 100件左右，2010年专利申请约为2 700件左右，其中，国外专利申请人轴承技术领域2009年专利申请约为300件左右，2010年专利申请约为350件左右。