信息熵在缺陷漏磁信号量化中的应用
2011-07-23赵海龙杨志军
戴 光,赵海龙,杨志军
(东北石油大学机械科学与工程学院,大庆 163318)
随着我国经济的发展和国家战略原油储备体系的建立,石油化工行业的储罐数量和容量迅猛增加,其安全性也得到人们的高度关注。漏磁检测以其具有易于实现自动化、可靠性较高等优点,在储罐底板检测中得到了广泛的应用。对检测做出评定的基础是漏磁信号,当今对漏磁信号的研究主要分为正问题与逆问题两个方向。漏磁检测的正问题是根据缺陷特征参数来评估漏磁场的大小;而逆问题则是指由漏磁信号包含的信息量化出缺陷的特征参数。
信息熵理论自从提出以来以其独特的优势在各个领域得到了广泛的应用。笔者以漏磁信号为基础,对检测得到的缺陷信号进行熵谱分析,并将缺陷信号的信息熵作为漏磁信号的一个特征量,用于漏磁信号的量化。最后通过理论分析与试验研究,证明了熵谱分析在漏磁信号量化过程中的可行性。
1 信息熵
信息是对事物状态的存在方式和相互联系进行描述的一组文字符号、语言、图像或情态。人们通过掌握的信息可以减少对客观事物的不确定程度。因此美国数学家、信息论的创始人Shannon曾在题为《通讯的数学理论》的论文中指出:“信息是用来消除随机不定性的东西”。可见信息与熵有着紧密的联系。1957年Jaynes对信息熵做了如下定义[1]:
假设某事件的可能结果和出现的几率如下:
X1,X2,……,X n可能结果
P1,P2,……,P n出现的几率

则相应的信息熵为:
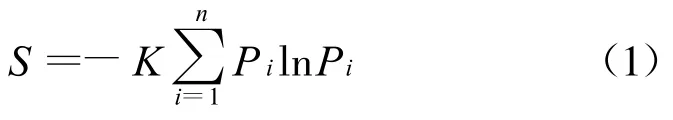
式中K为一比例系数。
若每个结果出现的几率相同:
P1=P2=……=Pi=……=P则式(1)变为:

式(2)中P表示任意结果出现的几率,若用 Ω表示可能出现的总数或微观状态数,且P=1/Ω,则式(2)转化成S=klnΩ,其中k称为玻尔兹曼常数,此时的熵往往被称为玻尔兹曼熵。当K取1/ln2时,S的单位为bit,此时的信息熵为:
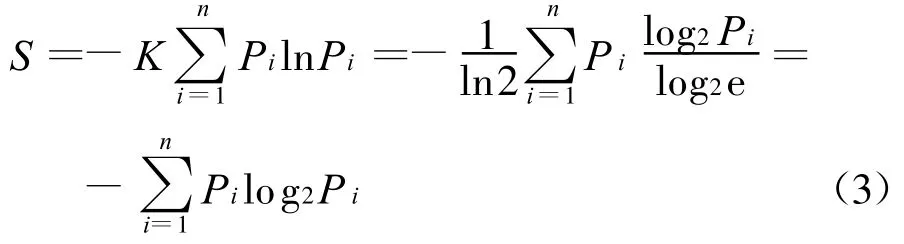
式(3)与Shannon提出的信息熵形式相同,故往往称此时的熵为Shannon熵。由上式可知,事情的可能性结果越多,每个结果出现的几率就越小,熵就越大,对事情的现状及发展变化越是难以判断。因此说,熵是无知度的度量。同时还可以发现,在Ω一定的情况下,当P1=P2=……=Pi=……=P时,事物的不确定程度最大,此时的信息熵也最大,对应的熵值为:

实际应用中,常常将式(3)与(4)之比作为信息的又一个度量,称之为相对信息熵,以H表示:

2 漏磁信号的信息熵
在现实应用中,常常根据信息熵的来源不同,将相应的信息熵分为不同种类,如由小波分解得到的信息熵称为小波熵;由FFT频谱分析得到的信息熵称为谱熵。而根据P的含义不同,又可将信息熵进行进一步分类,如同样由FFT分析得到的信息熵,当P反映FFT功率谱分布时则称对应的谱熵为功率谱熵;当P反映信号经过FFT变化后的幅值谱分布时,则称此时的谱熵为幅值谱熵。对应的相对熵则往往称为相对功率谱熵与相对幅值谱熵。2004年王太勇将相对功率谱熵引入到漏磁信号识别过程中,通过试验证明该特征量可以消除速度对漏磁信号的影响,进而可以区分不同种类的缺陷[2]。考虑到缺陷信号的相对幅值谱熵抗噪能力强,同时随缺陷尺寸的变化规律稳定且明显,笔者将缺陷信号的相对幅值谱熵[3]作为漏磁信号的一个特征量,用于漏磁信号的量化处理。该特征量计算过程为:
(1)确定缺陷信号的存在区间。
(2)将分析信号的基线置零:可以通过s′=s-获得 ,其中s为原始信号为的平均值为置零后的信号。
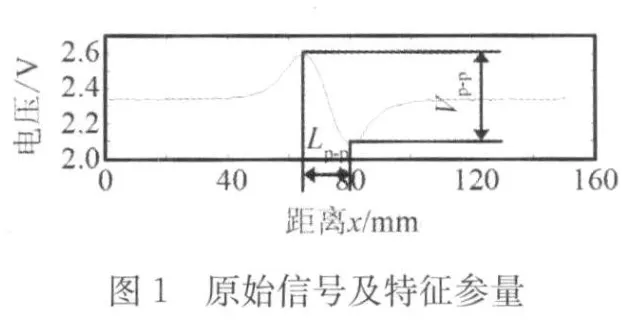
(3)对置零后的信号进行FFT变换(如图1和2),设经过FFT变换后得到信号的频谱序列为其中元素对应的频谱为。

(4)计算各个采集点对应的幅值谱熵:①计算各频谱的模,记为qj,则②计算各幅值的总和则该点对应的幅值谱熵为
(5)求信号总的幅值谱熵:
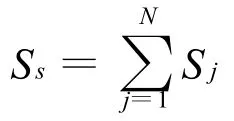
(6)计算信号的相对幅值谱熵:
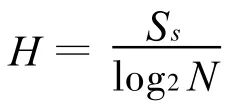
式中N为分析信号的长度。
当被测底板有缺陷时,漏磁信号的谱图往往会在某些频率或频段处出现能量集中。相对幅值谱熵反映了漏磁信号幅值谱的集中程度,熵值越小,幅值越集中;熵值越大,幅值越分散。在漏磁检测中,腐蚀缺陷越小,对应的缺陷信号越难从原始信号中区分出来,也就是说腐蚀缺陷尺寸越小,信号的不确定程度越大,信号越混乱,反映在熵领域中就是熵值越大;反之,腐蚀缺陷越大,缺陷信号越容易从原始信号中区分出来,不确定程度越小,对应的熵值也越小。所以可以用信号的相对幅值谱熵作为量化缺陷信号的一个特征量。
3 试验研究
定义缺陷的深度方向为垂直于平板的方向,缺陷的长度方向为检测仪的行走方向;量化的深度为缺陷的最大深度,量化的长度为沿检测仪行走方向各路传感器所对应的长度。为了便于信号的量化,笔者在该特征量的基础上又选择了缺陷信号的峰谷高值Vp-p和峰谷长值Lp-p(图1)作为缺陷信号的另外两个特征量,分别用于量化缺陷的长度与深度。采用BP网络来完成缺陷的量化过程,量化过程的信息流量如图3所示。
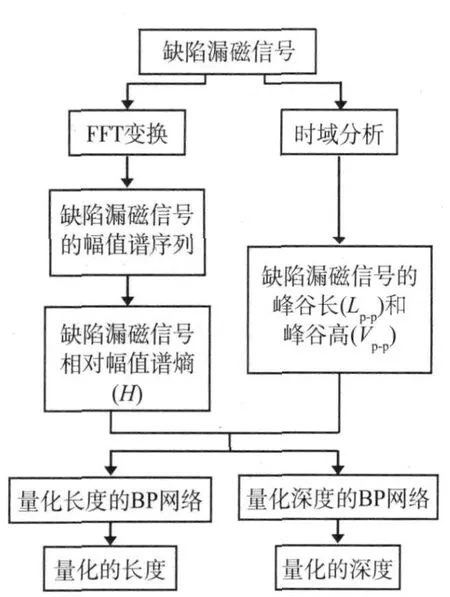
图3 信号处理流程
网络的训练及仿真样本来源于试验标定板。标定板板厚为6mm,在标定板上人为加工了大小不等的圆柱形缺陷28个,其按直径分为 5,10,15,20,25,30,35 mm共七组,每组有1,2,3,4 mm深四个圆柱形缺陷。利用30通道漏磁扫描检测仪对标定板进行检测。用Matlab软件按传感器通道对插值后的数据进行特征提取,最后可得595个样本。将其中的399个样本用于网络的训练,剩下的196个样本用于网络的仿真。网络训练的最大误差设定为1×10-5,笔者采用两个双隐层的BP网络分别量化缺陷的长度与深度,利用“试凑法”来确定中间隐层单元的神经元个数。最后确定深度方向的神经网络结构为3×12×15×1,长度方向的神经网络结构为3×10×11×1。此时长度方向与深度方向神经网络最低仿真精度分别为93.62%与97.60%。
对训练好的网络进行测试,测试数据来源于试验板,试验板的缺陷分布如图4所示。表1和2分别为两个网络的测试结果。
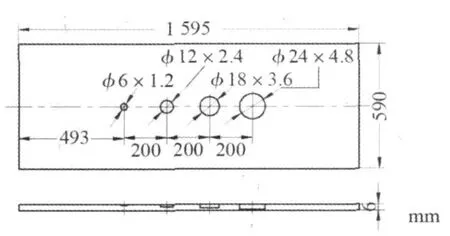
图4 试验板缺陷分布
由表1和表2可知,用该网络对缺陷进行量化,深度方向的精度最低可达84.17%,长度方向的精度最低可达88.48%。不难发现,网络的测试精度明显低于相应的仿真精度。这是因为通过训练,网络已经很好地掌握了标定板上缺陷与信号之间的对应关系,但由于制造、加工、测量等误差的存在以及来自平板本身(如表面粗糙度)、外界环境(如电磁波干扰)、人为等因素的影响,该对应关系在不同板上的表现形式存在差异。因此当用同一块板上的缺陷样本对网络进行仿真时,网络的量化精度很高;而用另一块板上的缺陷样本去测试网络性能时,网络的量化精度会下降,但该精度仍在可接受的范围之内。故可以将信息熵作为缺陷量化的一个特征量。
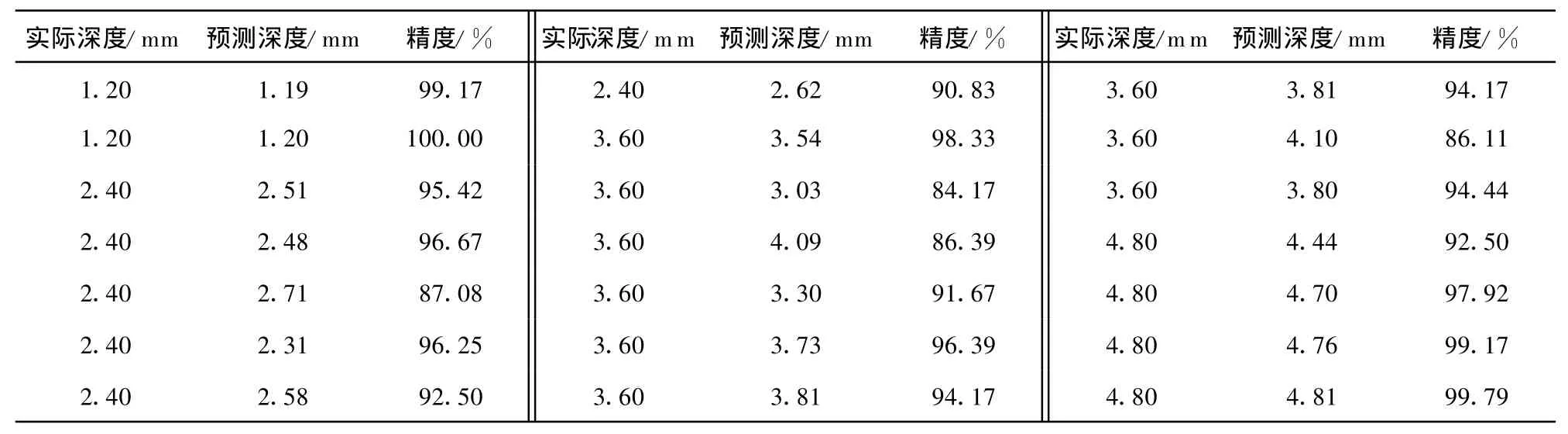
表1 缺陷深度量化结果
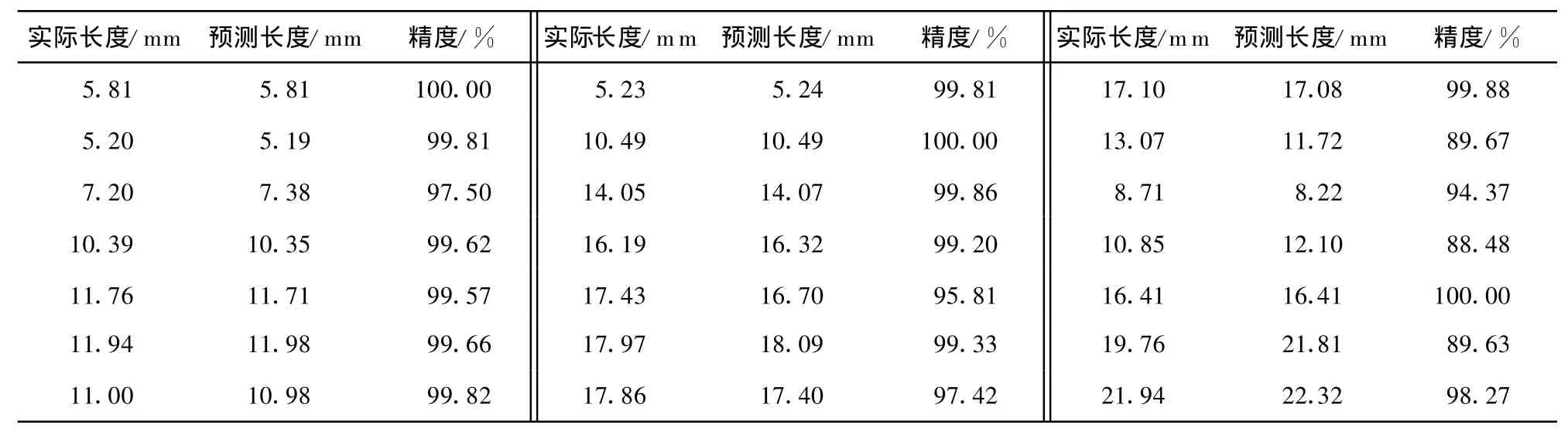
表2 缺陷长度量化结果
4 结论
(1)对缺陷漏磁信号进行了FFT变换,并根据变换后的幅值谱序列完成了缺陷漏磁信号信息熵的提取。
(2)建立了用于量化缺陷深度与长度两个方向的BP网络,并根据标定板数据完成了神经网络的训练与仿真。长度与深度两个方向的BP网络最低仿真精度分别达到了93.62%和97.60%。
(3)根据试验板数据对网络的性能进行了测试,深度方向神经网络的预测精度最低可达84.17%、长度方向神经网络的预测精度最低可达88.48%,故可以将缺陷信号的信息熵作为漏磁信号量化的一个特征量,用于漏磁信号的量化处理。
[1]李鹤龄.信息熵、玻尔兹曼熵以及克劳修斯熵之间的关系——兼论玻尔兹曼熵和克劳修斯熵是否等价[J].大学物理,2004,23(12):37-40.
[2]王太勇,刘兴荣,秦旭达,等.谱熵分析方法在漏磁信号特征提取中的应用[J].天津大学学报,2004,37(3):216-220.
[3]刘红星,左洪福,姜澄宇,等.信号频谱的二维向量及其应用[J].中国机械工程,1999,10(5):537-539.
