基于ANSYS的浮环动静压轴承中浮环的有限元分析
2011-07-21郭红陈昌婷岑少起
郭红,陈昌婷,岑少起
( 郑州大学 机械工程学院,郑州 450001)
浮环动静压轴承是在主轴与轴瓦之间加入一个浮环,主轴和浮环之间形成内膜,轴瓦和浮环之间形成外膜。轴承工作时,主轴以角速度Ω1旋转,通过油膜带动浮环以Ω2旋转,浮环的角速度系通过内、外油膜的作用力和摩擦力矩的平衡来调节。浮环降低了主轴和轴瓦的相对速度,能够有效控制高速轴承的摩擦功耗和温升[1]。动静压浮环轴承内、外层的油膜厚度都很小,最厚处一般不超过半毫米,最薄处仅有几微米。而浮环是一个很轻的薄壁零件,运转时受到内、外膜力和力矩的作用,当内、外膜作用到浮环的力和力矩相等时,浮环平衡。文献[2-5]对径推联合浮环动静压轴承特性参数及稳定性参数做了研究,文献[6-7]对错位浮环轴承等形状复杂的轴承性能作了分析。但是这些研究都是将浮环看作刚性元件,实际上浮环受力后会发生变形,即使浮环微小的变形也会影响内、外膜的油膜厚度,进而影响轴承的静、动特性参数。文献[8]探讨了动载轴承轴瓦合金层的应力变化,但没有涉及浮环。
下文以圆柱浮环动静压轴承为研究对象,建立内、外膜的压力控制方程、边界条件和流量平衡方程,通过有限元仿真得到内、外膜的压力分布。在此基础上,借助ANSYS有限元分析软件建立浮环的实体模型[9]。将压力及约束加载在浮环上,形成有限元模型,求解得到浮环的应力、应变云图,可以直观地看出浮环在油膜力作用下的变形。在此基础上探究浮环变形对油膜厚度的影响,分析何种工况下计算浮环轴承特性可以忽略浮环的变形。
1 浮环轴承控制方程及边界条件
图1为向心浮环轴承结构示意图,内膜采用4腔结构,外膜为5腔结构,每个腔都设置有深腔和浅腔。静压部分采用阶梯圆柱销节流方式[10]。周期性变化的油膜压力是引起浮环变形的主要原因,故计算中只考虑油膜压力的影响,即浮环内、外表面分别作用着内、外膜的油膜压力,将该油膜压力离散成有限元网格节点上的集中力。

图1 向心浮环轴承结构示意图
1.1 控制方程
(1)
式中:Di为轴承直径,mm;Li为轴承长度,mm;hi为油膜厚度,mm;μ为润滑油黏度,Pa·s;pi为油膜压力,MPa;ci为半径间隙,mm;Ω1为轴颈角速度,1/s;Ω2为浮环角速度,1/s;ps为供油压力,MPa;φi为圆周方向坐标;λ为浮环变形量与最小油膜厚度之比。凡下标i=1表示内膜参数,下标i=2表示外膜参数,其他未标注者同一般润滑理论规范。
1.2 边界条件
如图2所示,向心浮环轴承内、外膜满足如下压力边界条件和节流器流量平衡条件。

图2 向心浮环轴承压力边界条件及流量平衡条件
(2)

(3)
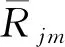
1.3 油膜厚度
内、外膜无量纲油膜厚度可表示为

无量纲最小油膜厚度为
(5)
式中:ei为偏心距,mm;θi为偏位角,(°);hsi为深腔深度,mm;hqi为浅腔深度,mm;hmin为最小油膜厚度,mm。
在建立浮环轴承控制方程、压力边界条件及节流器流量平衡方程基础上,用有限元法对各控制方程进行离散,计入压力边界条件和流量平衡条件,可得到内、外膜压力分布。
2 浮环有限元模型的建立
2.1 浮环实体模型的建立
浮环腔的深度相对于浮环的壁厚小很多,所以建模时将浮环简化,略去腔的结构。硬点是一种特殊的关键点,不改变模型的几何形状和拓扑结构,与普通关键点的区别在于划分网格之后硬点所在位置处必须产生节点。由于浮环承受的内、外膜的力将被离散成有限元网格上的节点力,所以建立硬点用于施加油膜力。最终建立的浮环实体模型如图3所示。
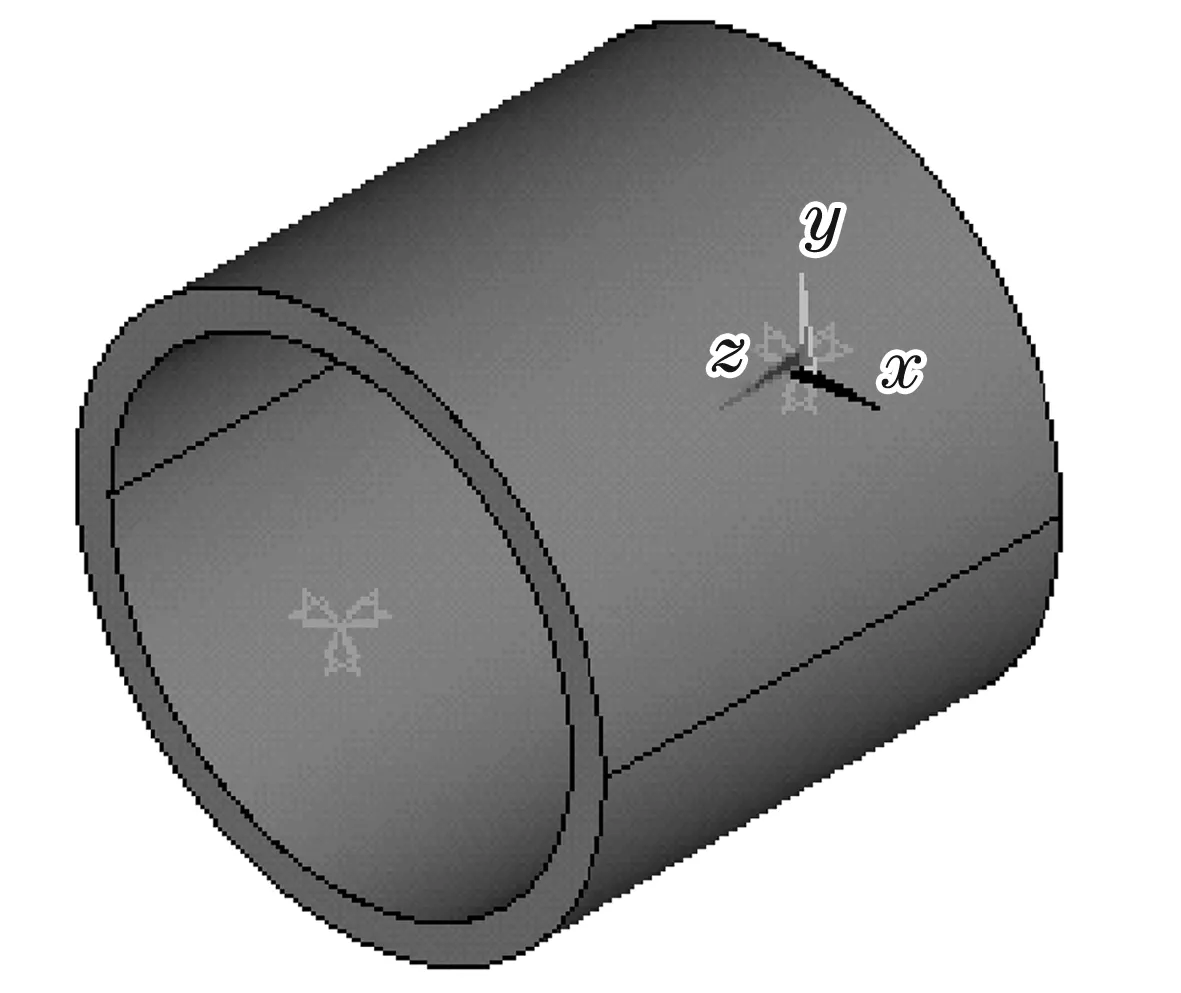
图3 浮环实体模型
2.2 浮环有限元网格划分
有限元网格划分是将整体结构离散化,是数值分析的前提。文中采用6面体8节点单元SOLID45对浮环进行网格划分。在定义网格尺寸时,可通过smart size进行调节。网格模型的节点数为21 334个,单元数为6 398个。划分网格APDL命令为:
MSHAPE, 1,3D
MSHKEY, 0
VMESH, ALL。
2.4 载荷及约束条件
将内、外膜的油膜力离散加载在节点上,并约束浮环两端面的平动自由度,最终得到浮环的有限元计算模型(图4)。
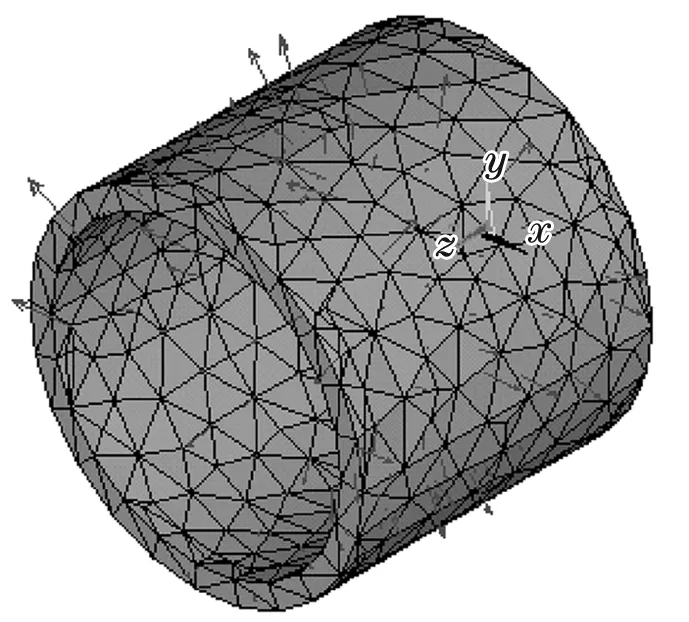
图4 浮环的有限元计算模型
3 计算结果及其分析
3.1 轴承结构参数及其运行条件
取润滑油黏度μ=4.475×10-3Pa·s;供油压力ps=1 MPa。浮环采用合金材料,弹性模量为2.1×105MPa,泊松比为0.29。浮环轴承结构参数如表1所示。分别取定外膜偏心率,通过调整内膜偏心率、浮环轴颈转速比使浮环达到平衡。

表1 向心浮环轴承结构参数
3.2 计算结果及分析
首先求解Reynolds方程和流量边界条件的联合方程组,得到内、外膜压力分布,即作用在浮环上的力。图5和图6为主轴转速为10 000 r/min、外膜偏心率为0.6时浮环平衡状态下内、外膜无量纲压力分布。
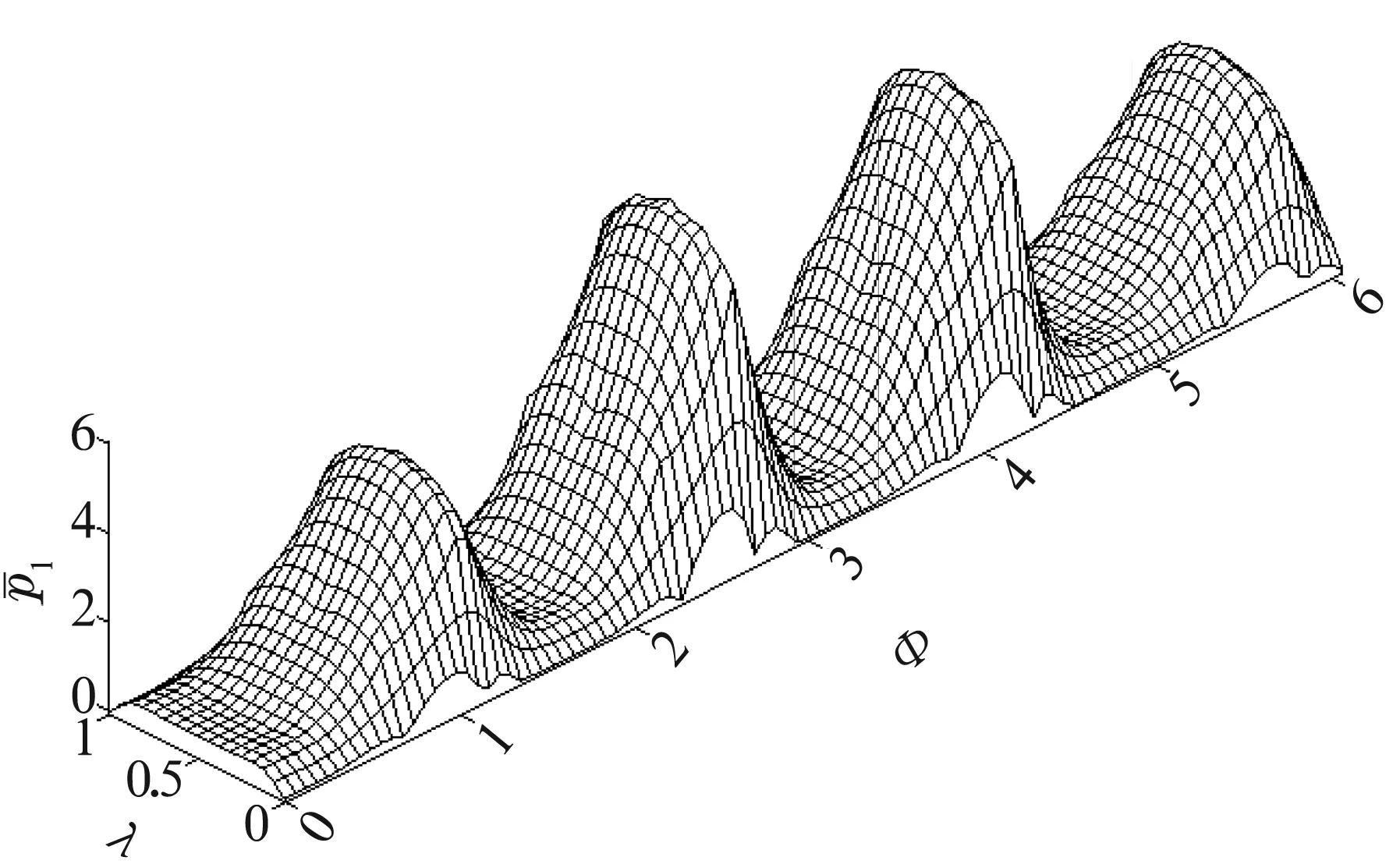
图5 内膜压力分布(Ω1=10 000 r/min,ε2=0.6)

图6 外膜压力分布( Ω1=10 000 r/min,ε2=0.6)
将内、外膜的油膜力离散加载在节点上,并约束浮环两端面的平动自由度。采用ANSYS计算不同转速、不同偏心率下浮环的变形量。图7和图8为外膜偏心率0.6、主轴转速10 000 r/min和60 000 r/mm时浮环总变形云图。可以看出,浮环受力变形与油膜的压力分布规律相似,在轴承的油腔周围对应的油膜力最大,变形也较大,而在轴承两端所承受的压力接近于大气压力,变形几乎为0。最大的变形量发生在浮环内膜的4个腔附近。
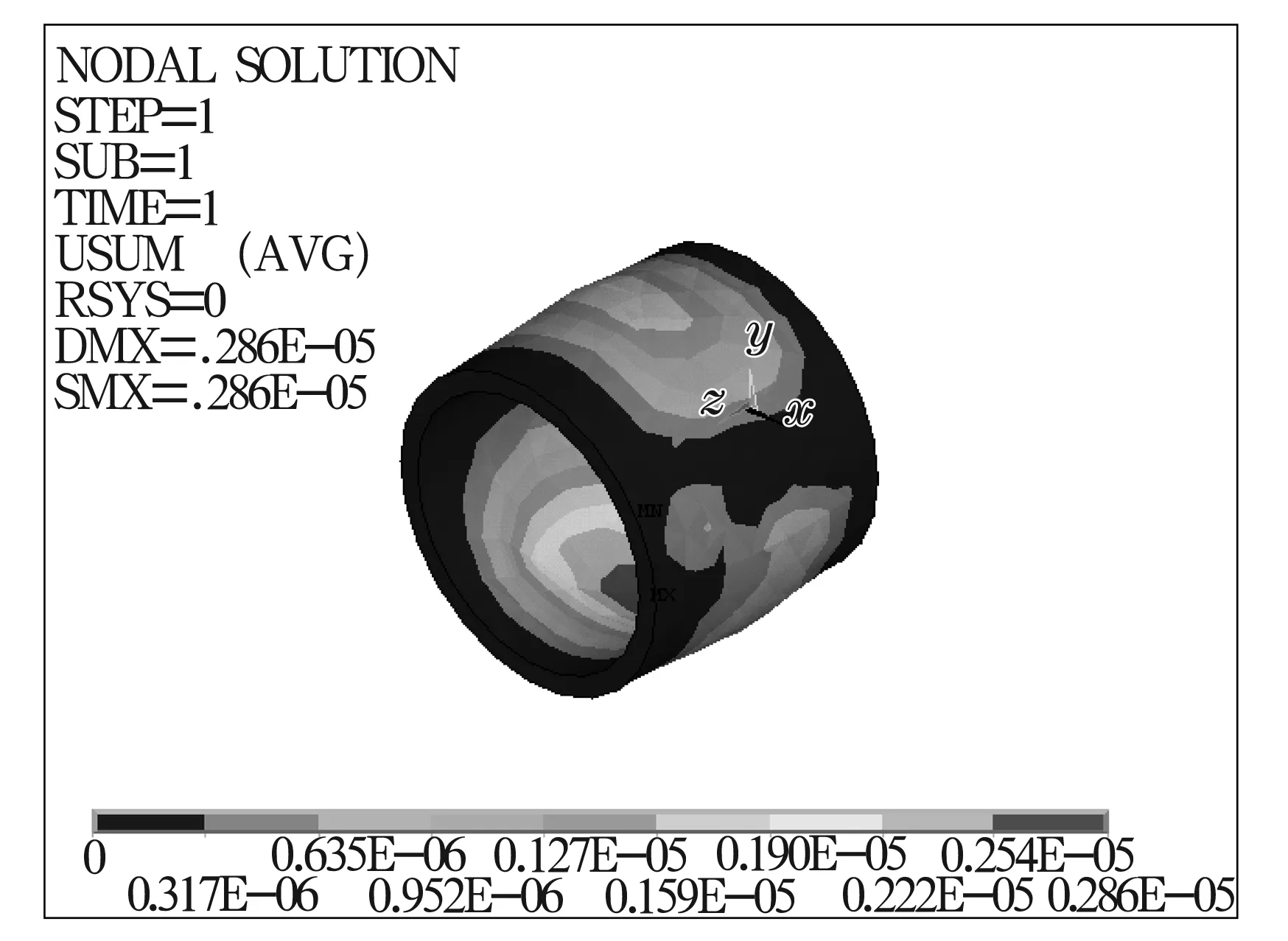
图7 浮环位移云图(Ω1=10 000 r/min,ε2=6)
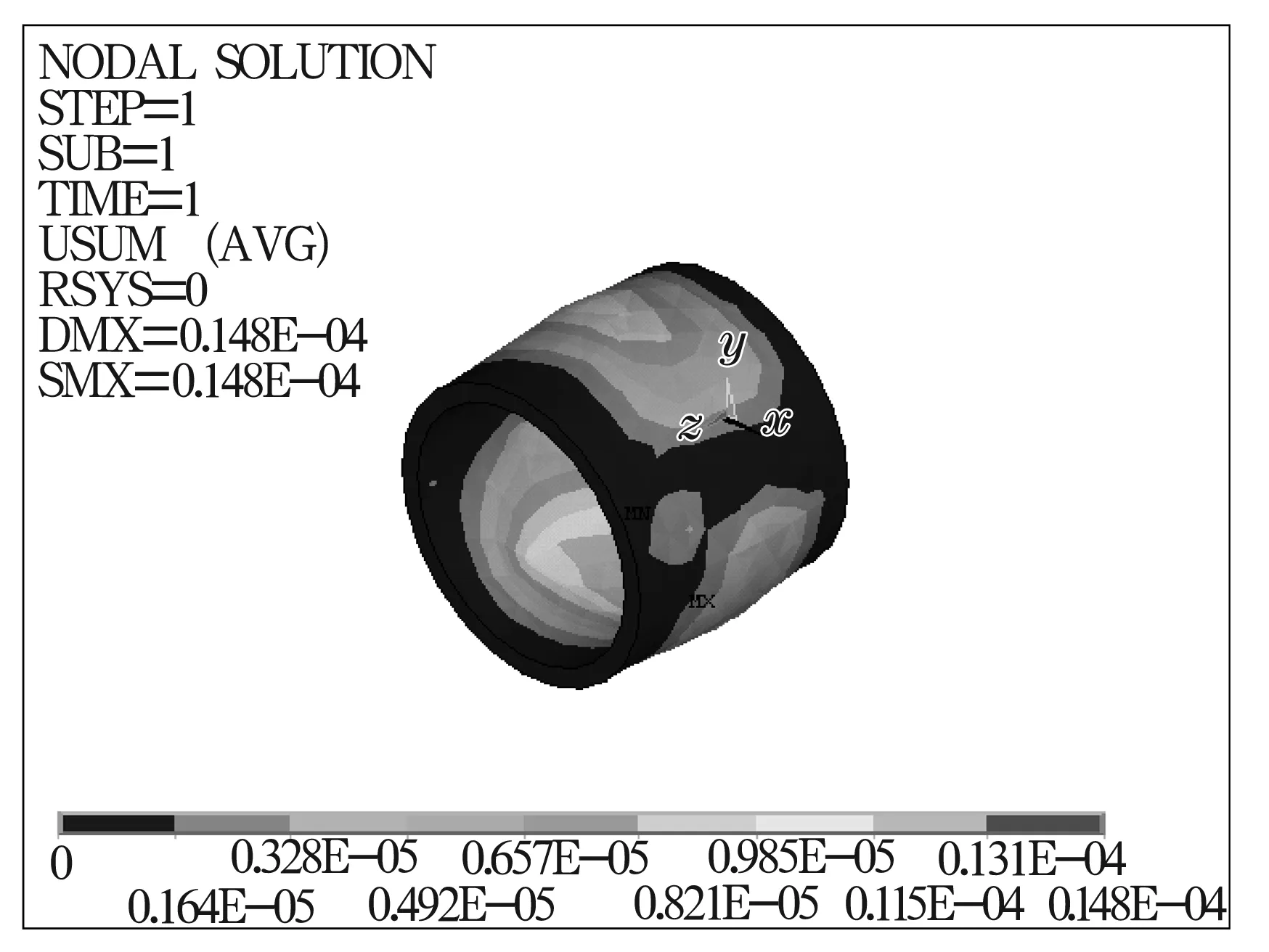
图8 浮环位移云图(Ω1=60 000 r/min,ε2=6)
图9为最小油膜厚度随偏心率的变化曲线,由图可以明显看出,随着偏心率的增大,最小油膜厚度迅速减小。图10为不同转速下浮环变形量随偏心率的变化曲线,可以看出,随着偏心率的增加,浮环变形亦增大;转速提高,动压效应增强,浮环变形量明显变大。图11为不同转速下浮环变形量与最小油膜厚度的比值,可以看出,在转速不太高、偏心率低于0.6时浮环的变形量相对于油膜厚度可以忽略不计,将浮环看作刚体进行研究可以满足要求;在转速较高、偏心率较大时,必须考虑浮环的变形量对油膜厚度的影响,对内、外层油膜厚度进行修正,继而得出更加符合实际情况的轴承油膜压力以及静、动特性参数。
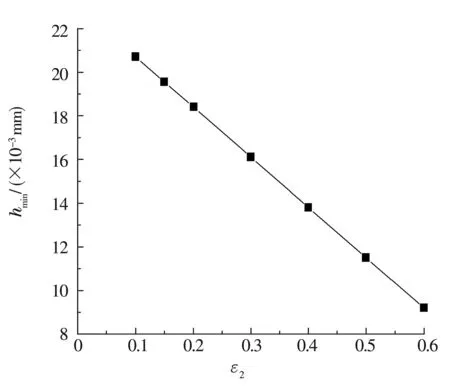
图9 最小油膜厚度随偏心率变化情况

图10 不同转速下浮环变形量随偏心率变化曲线

图11 不同转速下浮环变形量与最小油膜厚度之比
4 结束语
(1)浮环轴承内、外层油膜厚度均很小,浮环受力后产生的变形将影响油膜厚度。通过分析浮环在内、外膜压力作用下的变形情况得出:在转速不太高、偏心率低于0.6时浮环的变形量相对于油膜厚度可以忽略不计,为将浮环看作刚体提供了理论依据;而当转速较高、偏心率较大时,必须考虑浮环的变形量对油膜厚度的影响。
(2)借助于ANSYS的计算结果,可依照实际工况及浮环变形情况对内、外层的油膜厚度进行修正,继而得出更加符合实际情况的轴承油膜压力以及静、动特性参数,为计算浮环变形大小提供了一种方法。
